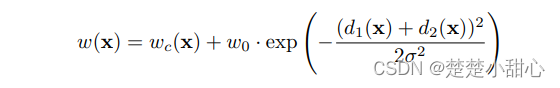1.反走样

1.1 什么是走样

在上一篇文章中，我们通过采样的方式把一个三角形变成离散的点显示在屏幕上。在采样过程中，我们会产生很多锯齿，这些锯齿的学名就叫做走样

1.2 反走样

如何消除锯齿(走样),我们就要引入反走样技术，之所以会产生走样的原因是因为采样的速度比信号频率慢，对于图像来说，信号代表的就是图片上的每个像素，而信号频率代表的是这个像素对于周围像素颜色差异的程度。

常见的走样分为以下几种：、

锯齿：空间上采样产生的走样；
摩尔纹：空间上下采样产生的走样；
车轮效应：时间上采样产生的走样。
这些我们也会称为采样的瑕疵（Artifacts）

1.3 反走样方法

为了能够减轻走样带来的影响，我们会对要采样的图形先进行模糊操作，再根据模糊后的图形进行采样，这就是反走样的过程。
在这里插入图片描述
为什么把一个图片模糊就可以解决锯齿问题？实际上在我们光栅化的过程中，采样的目的是为了用采样的像素来描述一个三角形，好那我举个例子，如果一个圆，我采样取四个点，那这四个点连起来实际上是个正方形，不能够准确描述这是个圆，那我提高采样频率，我采5个点，6个点，7…随之而来连接起来是5边形，6边形，7边形…随着采样的点(频率)数量越来越多，那么连接起来就越来越接近个圆，同样我们是不是可以提高采样率来抗锯齿，答案是可以的，但是我们不能要求你有抗锯齿就要求客户换一个分辨率更高的显示器，这是不合理的，那么相对的我不能提高采样率，那能不能降低信号频率，我们可以看到对于这个三角形信号频率最高的像素在三角形边缘，红色=>白色，颜色差异很大所以变化率高，但是我们通过模糊后的三角形边缘有了渐变效果实际上就是降低了信号频率，从而实现的抗锯齿效果。当然这是大白话，在数学上我们会有更抽象的证明方式，往后看。

1.4 傅里叶变换

任何一个信号都可以表示为一些正弦波和余弦波以及常数的线性表示，我们称之为傅立叶展开。而傅立叶变换指的是将一个时域上的信号转换到频域的过程。

1.5走样和滤波

走样更为学术的定义应该是两个不同频率的信号在使用相同采样的方法后产生的结果无法进行区分
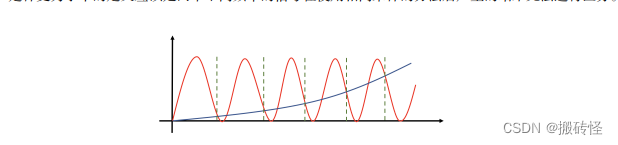
在这里插入图片描述
图中的红色信号和蓝色信号是两个频率不一样的信号，绿色虚线处是采样点，我们发现两个不同频率的信号在同一个采样方式下结果相同，这就产生了走样。

滤波是把特定频率的波过滤掉。如果仅保留高频信息，那么这称为高通滤波；如果仅保留低频信息称为低通滤波；如果既删除高频信息，还删除低频信息，只保留中频信息称为带通滤波。

在这里插入图片描述
对于一个图片我们进行傅立叶变换后，得到的是上面右图的样子。我们进行解释：中心代表了低频信息，边缘代表了高频信息，亮度代表对应频率的能量。对于图片而言，一般低频信息更加的丰富，而高频信息比较少。高频信息一般代表边缘信息，因为边缘信息频率比较高；低频信息是图片模糊后的结果，频率变化小。

为什么傅立叶变换后图片有一束明显的十字交叉？

傅立叶变换中我们会认为图片是“连续”的。我们会在原图上下左右不断重复图片以达到“连续”的效果。而图片的四周一般变换非常的快，属于高频的信息，对应在频谱图上就是会有一束明显的十字交叉，代表了高频的边缘信息。

1.6 卷积和卷积定律

滤波可以看作卷积操作，也可以看作平均操作。卷积（Convolution）操作是用一个卷积核在信号上不断地滑动，每一次卷积操作的结果是卷积核和对应位置信号乘积的和，可以看作一次加权平均的过程。

注：时域上的卷积等于频域上的乘积，频域上的乘积等于时域上的卷积。

1.6.1 Box Filter

Box Filter 是一个格式如下的滤波器：
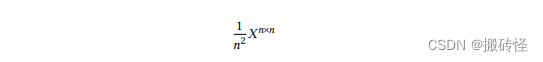
在这里插入图片描述
其中，𝑋 是一个全 1 矩阵。这个卷积核对临近的 𝑛 × 𝑛 的像素做平均。𝑛 越大，滤波器得到的频率范围越低。

2.深入了解采样

采样我们可以认为是一个连续函数乘以一系列的脉冲函数的结果。根据卷积定律我们知道，这相当于连续函数的傅立叶变换和脉冲函数傅立叶变换的卷积。脉冲函数的傅立叶变换还是脉冲函数。卷积的结果是信号的频谱在不断地重复。
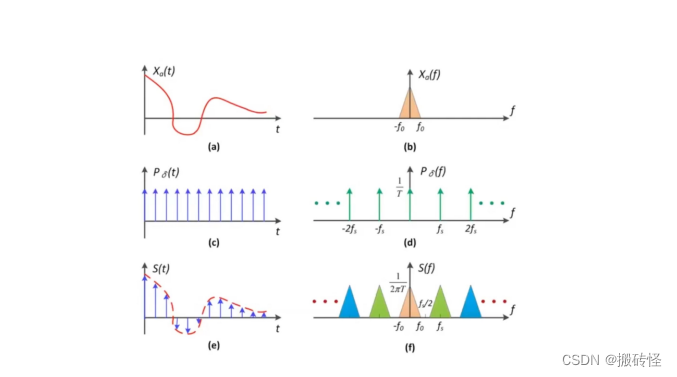
在这里插入图片描述
当采样率不足时会使得频谱之间的间隔太小，导致频谱间产生重叠，这些重叠就是走样。

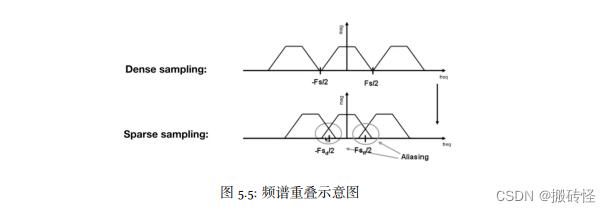
这也就解释了为什么使用低通滤波器可以帮助我们减少走样。这是因为使用低通滤波器只保留更窄的频率范围(干掉高频)，可以减少频谱的重叠。