1、含冷冻期 的多状态 买卖股票问题
1.1 leetcode 309:最佳买卖股票时机含冷冻期
第一遍代码
运用之前二维dp数组的方法,第二个维度大小为2,对应持有,不持有
dp[1][0] = max(dp[0][0], -prices[1]);注意要考虑只有一天的情况
dp[i][0] = max(dp[i - 1][0], dp[i - 2][1] - prices[i]);因为有冷冻期,所以是i - 2
class Solution {
public:
int maxProfit(vector<int>& prices) {
//运用之前二维dp数组的方法,第二个维度大小为2,对应持有,不持有
vector<vector<int>> dp(prices.size(), vector<int>(2));
dp[0][0] = -prices[0];
if(prices.size() > 1) {
dp[1][0] = max(dp[0][0], -prices[1]);//注意要考虑只有一天的情况
}
dp[0][1] = 0;
for(int i = 1; i < prices.size(); i++) {
if(i > 1) {
dp[i][0] = max(dp[i - 1][0], dp[i - 2][1] - prices[i]);//因为有冷冻期,所以是i - 2
}
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
}
return dp[prices.size() - 1][1];
}
};
1.2 leetcode 309:每天分为了4个状态
代码随想录思路(与第一遍代码思路不同,将每天分为了4个状态)
相对于 leetcode 122:买卖股票的最佳时机II ,本题加上了一个冷冻期
在 leetcode 122:买卖股票的最佳时机II 中有两个状态,持有股票后的最多现金,和不持有股票的最多现金
动规五部曲,分析如下:
1、确定dp数组以及下标的含义
dp[i][j],第i天状态为j,所剩的最多现金为dp[i][j]
因为出现冷冻期之后,状态其实是比较复杂度,例如今天买入股票、今天卖出股票、今天是冷冻期,都是不能操作股票的
具体可以区分出如下四个状态:
状态一:持有股票状态(今天买入股票,或者是之前就买入了股票然后没有操作,一直持有)
不持有股票状态,这里就有两种卖出股票状态
状态二:保持卖出股票的状态(两天前就卖出了股票,度过一天冷冻期。或者是前一天就是卖出股票状态,一直没操作)
状态三:今天卖出股票
状态四:今天为冷冻期状态,但冷冻期状态不可持续,只有一天
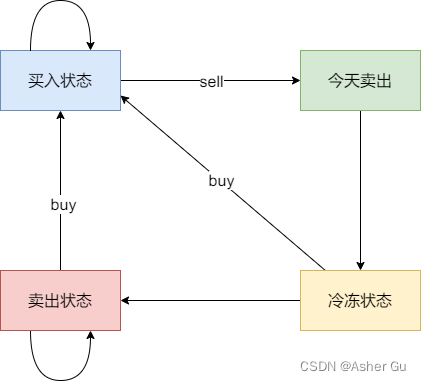
j的状态为:
0:状态一
1:状态二
2:状态三
3:状态四
在之前的题目中,「今天卖出股票」我是没有单独列出一个状态的归类为「不持有股票的状态」,而本题为什么要单独列出「今天卖出股票」 一个状态呢
因为本题我们有冷冻期,而冷冻期的前一天,只能是 「今天卖出股票」 状态,如果是 「不持有股票状态」那么就很模糊,因为不一定是 卖出股票的操作
注意这里的每一个状态,例如状态一,是持有股票状态并不是说今天一定就买入股票,而是说保持买入股票的状态即:可能是前几天买入的,之后一直没操作,所以保持买入股票的状态
2、确定递推公式
达到买入股票状态(状态一)即:dp[i][0],有两个具体操作(来源):
操作一:前一天就是持有股票状态(状态一),dp[i][0] = dp[i - 1][0]
操作二:今天买入了,有两种情况
前一天是冷冻期(状态四),dp[i - 1][3] - prices[i]
前一天是保持卖出股票的状态(所以需要区别保持卖出 和 今天卖出)(状态二),dp[i - 1][1] - prices[i]
那么dp[i][0] = max(dp[i - 1][0], dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i]);
达到保持卖出股票状态(状态二)即:dp[i][1],有两个具体操作啊(来源):
操作一:前一天就是状态二
操作二:前一天是冷冻期(状态四)
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
达到今天就卖出股票状态(状态三),即:dp[i][2] ,只有一个操作(来源):
昨天一定是持有股票状态(状态一),今天卖出
即:dp[i][2] = dp[i - 1][0] + prices[i];
达到冷冻期状态(状态四),即:dp[i][3],只有一个操作(来源):
昨天卖出了股票(状态三)
dp[i][3] = dp[i - 1][2];
综上分析,递推代码如下:
dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3], dp[i - 1][1]) - prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
dp[i][2] = dp[i - 1][0] + prices[i];
dp[i][3] = dp[i - 1][2];
3、dp数组如何初始化
这里主要讨论一下第0天(因为递推公式只与 上一个状态 有关)如何初始化
如果是持有股票状态(状态一)那么:dp[0][0] = -prices[0],一定是当天买入股票
保持卖出股票状态(状态二),这里其实从「状态二」的定义来说 ,很难明确应该初始多少,这种情况我们就看递推公式需要我们给他初始成什么数值
如果i为1,第1天买入股票,那么递归公式中需要计算 dp[i - 1][1] - prices[i] ,即 dp[0][1] - prices[1],那么大家感受一下 dp[0][1] (即第0天的状态二)应该初始成多少,只能初始为0。想一想如果初始为其他数值,是我们第1天买入股票后 手里还剩的现金数量是不是就不对了
今天卖出了股票(状态三),同上分析,dp[0][2]初始化为0,dp[0][3]也初始为0
4、确定遍历顺序
从递归公式上可以看出,dp[i] 依赖于 dp[i-1],所以是从前向后遍历
5、举例推导dp数组
以 [1,2,3,0,2] 为例,dp数组如下:
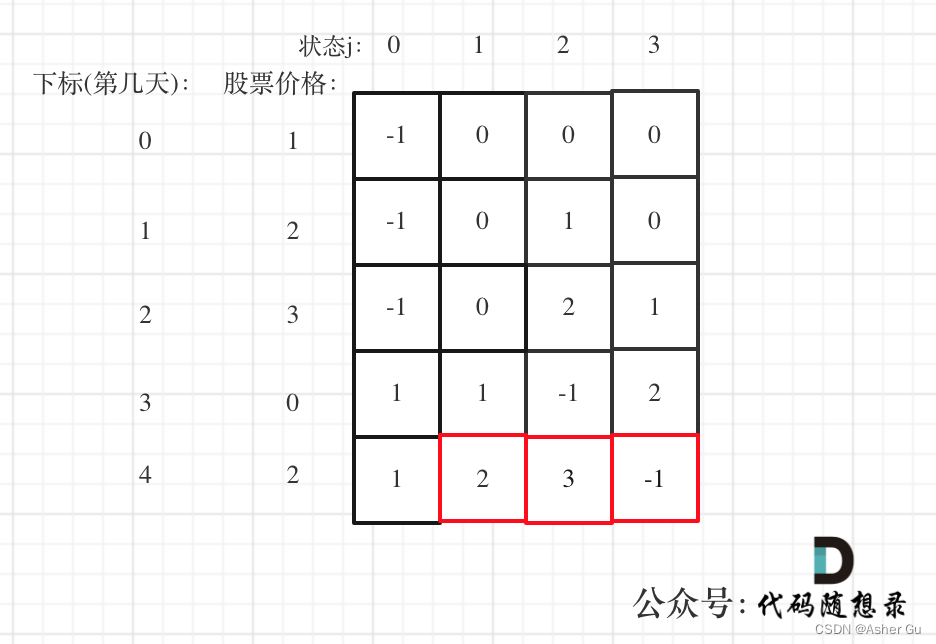
最后结果是取 状态二,状态三,和状态四的最大值,不少同学会把状态四忘了,状态四是冷冻期,最后一天如果是冷冻期也可能是最大值
代码如下:
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
if (n == 0) return 0;
vector<vector<int>> dp(n, vector<int>(4, 0));
dp[0][0] -= prices[0]; // 持股票
for (int i = 1; i < n; i++) {
dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i]));
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
dp[i][2] = dp[i - 1][0] + prices[i];
dp[i][3] = dp[i - 1][2];
}
return max(dp[n - 1][3], max(dp[n - 1][1], dp[n - 1][2]));
}
};
时间复杂度:O(n)
空间复杂度:O(n)
当然,空间复杂度可以优化,定义一个dp[2][4]大小的数组就可以了,就保存前一天的当前的状态
2、包含手续费 的买卖股票问题
2.1 leetcode 714:买卖股票的最佳时机含手续费
第一遍代码
只要在股票卖出的时候减去手续费就行
class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
//只要在股票卖出的时候减去手续费就行
vector<vector<int>> dp(prices.size(), vector<int>(2));
dp[0][0] = -prices[0];
dp[0][1] = 0;
for(int i = 1; i < prices.size(); i++) {
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);
}
return dp[prices.size() - 1][1];
}
};
代码随想录思路:
2.2 leetcode 714:贪心算法
在 leetcode 122:买卖股票的最佳时机II 中使用贪心策略不用关心具体什么时候买卖,只要收集每天的正利润,最后稳稳的就是最大利润了
而本题有了手续费,就要关心什么时候买卖了,因为计算所获得利润,需要考虑买卖利润可能不足以手续费的情况
如果使用贪心策略,就是最低值买,最高值(如果算上手续费还盈利)就卖
此时无非就是要找到两个点,买入日期,和卖出日期
买入日期:其实很好想,遇到更低点就记录一下
卖出日期:这个就不好算了,但也没有必要算出准确的卖出日期,只要当前价格大于(最低价格+手续费),就可以收获利润,至于准确的卖出日期,就是连续收获利润区间里的最后一天(并不需要计算是具体哪一天)
所以我们在做收获利润操作的时候其实有三种情况:
情况一:收获利润的这一天并不是收获利润区间里的最后一天(不是真正的卖出,相当于持有股票),所以后面要继续收获利润
情况二:前一天是收获利润区间里的最后一天(相当于真正的卖出了),今天要重新记录最小价格了
情况三:不作操作,保持原有状态(买入,卖出,不买不卖)
贪心算法C++代码如下:
class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
int result = 0;
int minPrice = prices[0]; // 记录最低价格
for (int i = 1; i < prices.size(); i++) {
// 情况二:相当于买入
if (prices[i] < minPrice) minPrice = prices[i];
// 情况三:保持原有状态(因为此时买则不便宜,卖则亏本)
if (prices[i] >= minPrice && prices[i] <= minPrice + fee) {
continue;
}
// 计算利润,可能有多次计算利润,最后一次计算利润才是真正意义的卖出
if (prices[i] > minPrice + fee) {
result += prices[i] - minPrice - fee;
minPrice = prices[i] - fee; // 情况一,这一步很关键,避免重复扣手续费
}
}
return result;
}
};
时间复杂度:O(n)
空间复杂度:O(1)
从代码中可以看出对情况一的操作,因为如果还在收获利润的区间里,表示并不是真正的卖出,而计算利润每次都要减去手续费,所以要让minPrice = prices[i] - fee;,这样在明天收获利润的时候,才不会多减一次手续费
会不会对买入中的prices[i] < minPrice 和 保持原有状态prices[i] >= minPrice && prices[i] <= minPrice + fee产生影响?不会,因为最后一次卖出的价格本来就要考虑需要减手续费,而对于result的计算来说,在整个持有过程中又只有第一天扣了手续费
2.3 leetcode 714:动态规划
相对于 leetcode 122:买卖股票的最佳时机II ,本题只需要在计算卖出操作的时候减去手续费就可以了,代码几乎是一样的
唯一差别在于递推公式部分,所以本篇也就不按照动规五部曲详细讲解了,主要讲解一下递推公式部分
这里重申一下dp数组的含义:
dp[i][0] 表示第i天持有股票所省最多现金。 dp[i][1] 表示第i天不持有股票所得最多现金
如果第i天持有股票即dp[i][0], 那么可以由两个状态推出来
第i-1天就持有股票,那么就保持现状,所得现金就是昨天持有股票的所得现金 即:dp[i - 1][0]
第i天买入股票,所得现金就是昨天不持有股票的所得现金减去 今天的股票价格 即:dp[i - 1][1] - prices[i]
所以:dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
在来看看如果第i天不持有股票即dp[i][1]的情况, 依然可以由两个状态推出来
第i-1天就不持有股票,那么就保持现状,所得现金就是昨天不持有股票的所得现金 即:dp[i - 1][1]
第i天卖出股票,所得现金就是按照今天股票价格卖出后所得现金,注意这里需要有手续费了即:dp[i - 1][0] + prices[i] - fee
所以:dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);
本题和 leetcode 122:买卖股票的最佳时机II 的区别就是这里需要多一个减去手续费的操作
跟第一遍代码思路相同,代码随想录C++代码如下:
class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
int n = prices.size();
vector<vector<int>> dp(n, vector<int>(2, 0));
dp[0][0] -= prices[0]; // 持股票
for (int i = 1; i < n; i++) {
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);
}
return max(dp[n - 1][0], dp[n - 1][1]);
}
};
时间复杂度:O(n)
空间复杂度:O(n)
对空间进行优化,因为当前状态只是依赖前一个状态
class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
int n = prices.size();
int holdStock = (-1) * prices[0]; // 持股票
int saleStock = 0; // 卖出股票
for (int i = 1; i < n; i++) {
int previousHoldStock = holdStock;
holdStock = max(holdStock, saleStock - prices[i]);
saleStock = max(saleStock, previousHoldStock + prices[i] - fee);
}
return saleStock;
}
};
时间复杂度:O(n)
空间复杂度:O(1)