文章目录
- 如何构造哈夫曼树
- 哈夫曼树构造算法的实现
如何构造哈夫曼树
哈夫曼算法口诀:
1.构造森林全是根;2.选用两小造新树;
3.删除两小添新人;4.重复2,3剩单根;
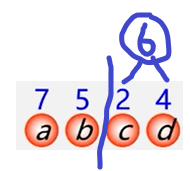
例:有4个新结点a,b,c,d,权值为7,5,2,4,构造哈夫曼树。

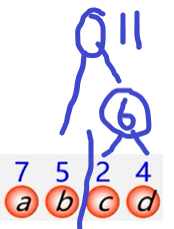

总结:
哈夫曼树中只有度为0或2,没有度为1的结点。
包含n个叶子结点的哈夫曼树共有2n-1个结点。
例:有5个结点a,b,c,d,e,权值分别为7,5,5,2,4.构造哈夫曼树。
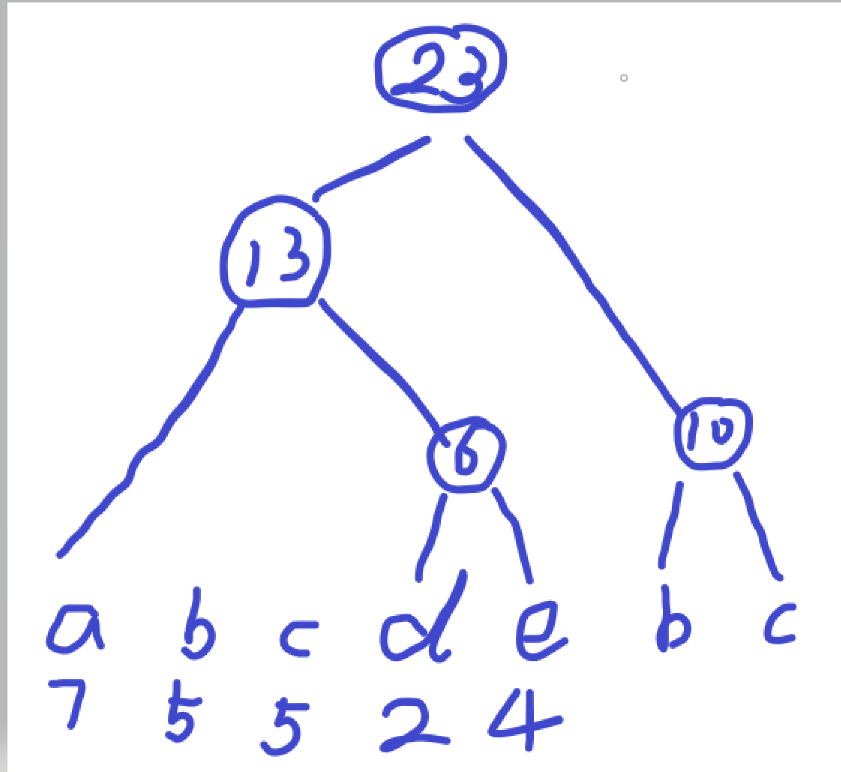
哈夫曼树构造算法的实现
1.初始化HT:lch=rch=parent=0;
2.输入n个叶子结点:置为HT[1…n]的weight值;
3.在进行n-1次合并,依次产生n-1个结点HT[i],i= n+1…2n-1;
a)在HT[1…i-1]中选两个未被选中(从parent == 0的结点中选)的weight最小的两个结点HT[s1]和HT[s2],s1,s2为两个最小结点的下标;
b)修改HT[s1]和HT[s2]的parent值:HT[s1].parent=i;HT[s2].parent=i;
c)修改新产生的HT[i]:
- HT[i].weight=HT[s1].weight+HT[s2].weight;
- HT[i[.lch=s1;HT[i].rch=s2;
typedef struct {
char data;//结点的数据
int parent, lch, rch;//双亲结点和孩子结点的下标
int weight;//权值
}htNode,*HuffmanTree;
//构造哈夫曼树----哈夫曼算法
int CreateHuffmanTree(HuffmanTree HT,int n) {
int m,i;
if (n <= 1) {
return;
}
m = 2 * n - 1;//数组共2n-1个元素
HT = new htNode[m + 1];//0号单元未用,HT[m]表示根结点
for (i = 1; i <= m; ++i) {
//将2n-1个元素的lch,rch,parent置为0
HT[i].lch = 0;
HT[i].rch = 0;
HT[i].parent = 0;
}
cout << "初始化成功" << endl;
for (i = 1; i <= n; ++i) {
cin >> HT[i].weight;//输入前n个元素的weight值
//初始化结束,下面开始建立哈夫曼表
}
for (i = n + 1; i <= m; i++) {//合并产生-1个结点,构造Huffman树
//Select(HT, i - 1, s1, s2);
HT[s1].parent = i;//表示从F中删除s1,s2
HT[s2].parent = i;
//s1,s2分别作为i的左右孩子
HT[i].lch = s1;
HT[i].rch = s2;
//i的权值为左右孩子权值之和
HT[i].weight = HT[s1].weight + HT[s2].weight;
}
}