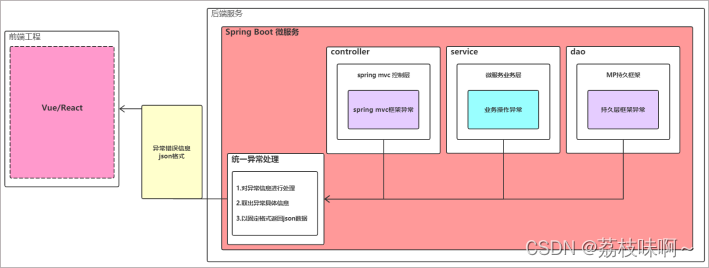
多维数据分析是对数据的信息分析,它考虑了许多关系。让我们来介绍一些使用Python分析多维/多变量数据的基本技术。
从这里找到用于说明的数据的链接。(https://archive.ics.uci.edu/dataset/111/zoo)
以下代码用于从zoo_data. csv读取2D表格数据。
import pandas as pd
zoo_data = pd.read_csv("zoo_data.csv", encoding = 'utf-8',
index_col = ["animal_name"])
# print first 5 rows of zoo data
print(zoo_data.head())
输出

**注意:**我们这里的数据类型通常是分类的。本案例研究中使用的分类数据分析技术是非常基本的,易于理解,解释和实施。这些方法包括聚类分析、相关分析、PCA(主成分分析)和EDA(探索性数据分析)。
聚类分析
由于我们拥有的数据是基于不同类型动物的特征,我们可以使用一些众所周知的聚类技术将动物分为不同的组(簇)或子组,即KMeans聚类,DBscan,层次聚类和KNN(K-Nearest Neighbours)聚类。为了简单起见,在这种情况下,KMeans聚类应该是一个更好的选择。使用Kmeans聚类技术对数据进行聚类,可以使用sklearn库聚类类的KMeans模块实现,如下所示:
# from sklearn.cluster import KMeans
clusters = 7
kmeans = KMeans(n_clusters = clusters)
kmeans.fit(zoo_data)
print(kmeans.labels_)
输出

inertia表示的是每个样本点到其所在质心的距离之和。按照inertia的定义来说inertia是越小越好。
在这里,总的集群inertia是119.70392382759556。
EDA分析
为了执行EDA分析,我们需要将多变量数据降维为三变量/双变量(2D/3D)数据。我们可以使用PCA(主成分分析)来实现这个任务。
可以使用sklearn库的类分解的PCA模块进行PCA,如下所示:
# from sklearn.decomposition import PCA
pca = PCA(3)
pca.fit(zoo_data)
pca_data = pd.DataFrame(pca.transform(zoo_data))
print(pca_data.head())
输出

上面的数据输出表示简化的三变量(3D)数据,我们可以在其上执行EDA分析。
注意: PCA产生的简化数据可间接用于执行各种分析,但不能直接由人类解释。
散点图是一种2D/3D图,有助于分析2D/3D数据中的各种聚类。
我们之前制作的3D简化数据的散点图可以绘制如下:
下面的代码是一个Python代码,它生成一个颜色数组(其中颜色的数量大约等于聚类的数量),按照色调,值和饱和度值的顺序进行排序。这里,每种颜色与单个聚类相关联,并将用于将动物表示为3D点,同时将其绘制在3D图/空间中(本例中为散点图)。
from matplotlib import colors as mcolors
import math
''' Generating different colors in ascending order
of their hsv values '''
colors = list(zip(*sorted((
tuple(mcolors.rgb_to_hsv(
mcolors.to_rgba(color)[:3])), name)
for name, color in dict(
mcolors.BASE_COLORS, **mcolors.CSS4_COLORS
).items())))[1]
# number of steps to taken generate n(clusters) colors
skips = math.floor(len(colors[5 : -5])/clusters)
cluster_colors = colors[5 : -5 : skips]
下面的代码是一个pythonic代码,它生成一个3D散点图,其中每个数据点都有一个与其对应的聚类相关的颜色。
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111, projection = '3d')
ax.scatter(pca_data[0], pca_data[1], pca_data[2],
c = list(map(lambda label : cluster_colors[label],
kmeans.labels_)))
str_labels = list(map(lambda label:'% s' % label, kmeans.labels_))
list(map(lambda data1, data2, data3, str_label:
ax.text(data1, data2, data3, s = str_label, size = 16.5,
zorder = 20, color = 'k'), pca_data[0], pca_data[1],
pca_data[2], str_labels))
plt.show()
输出
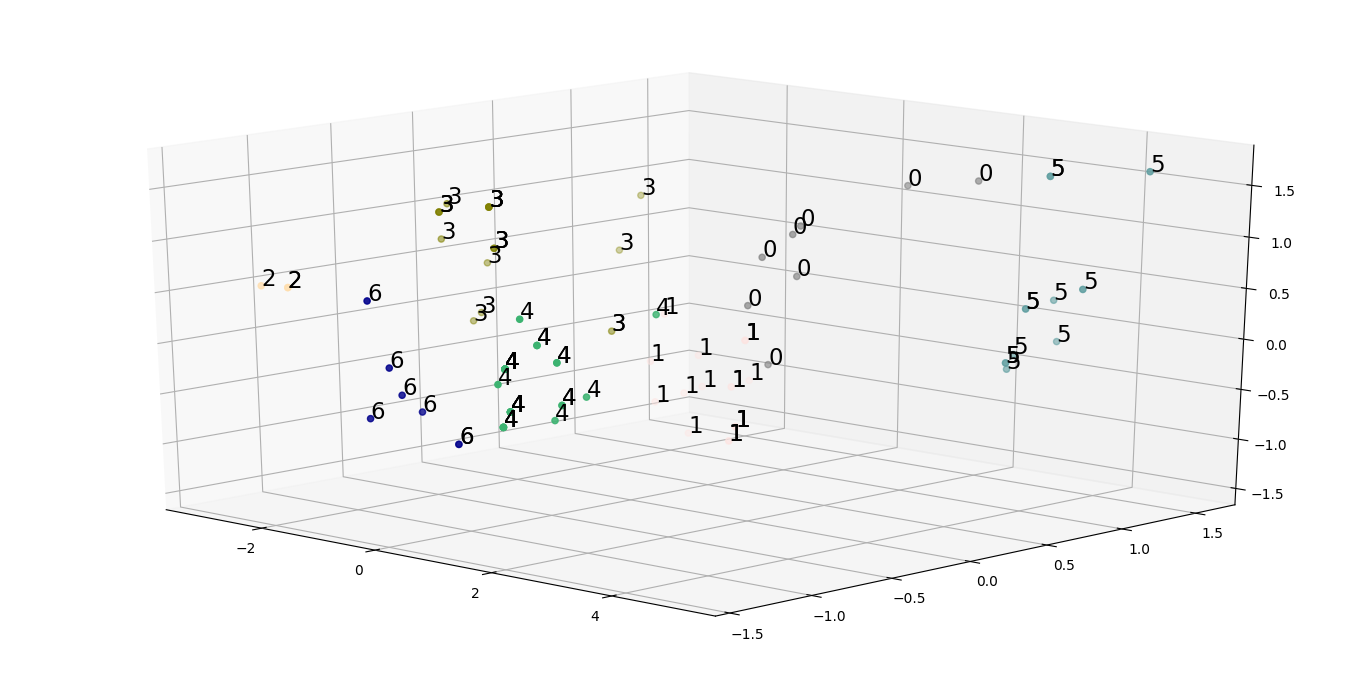
仔细分析散点图可以得出这样的假设,即使用初始数据形成的聚类没有足够好的解释力。为了解决这个问题,我们需要将我们的特征集降低到一个更有用的特征集,使用它我们可以生成有用的聚类。产生这样一组特征的一种方法是进行相关性分析。这可以通过如下绘制热图和3d图来完成:
import seaborn as sns
# generating correlation heatmap
sns.heatmap(zoo_data.corr(), annot = True)
# posting correlation heatmap to output console
plt.show()
输出
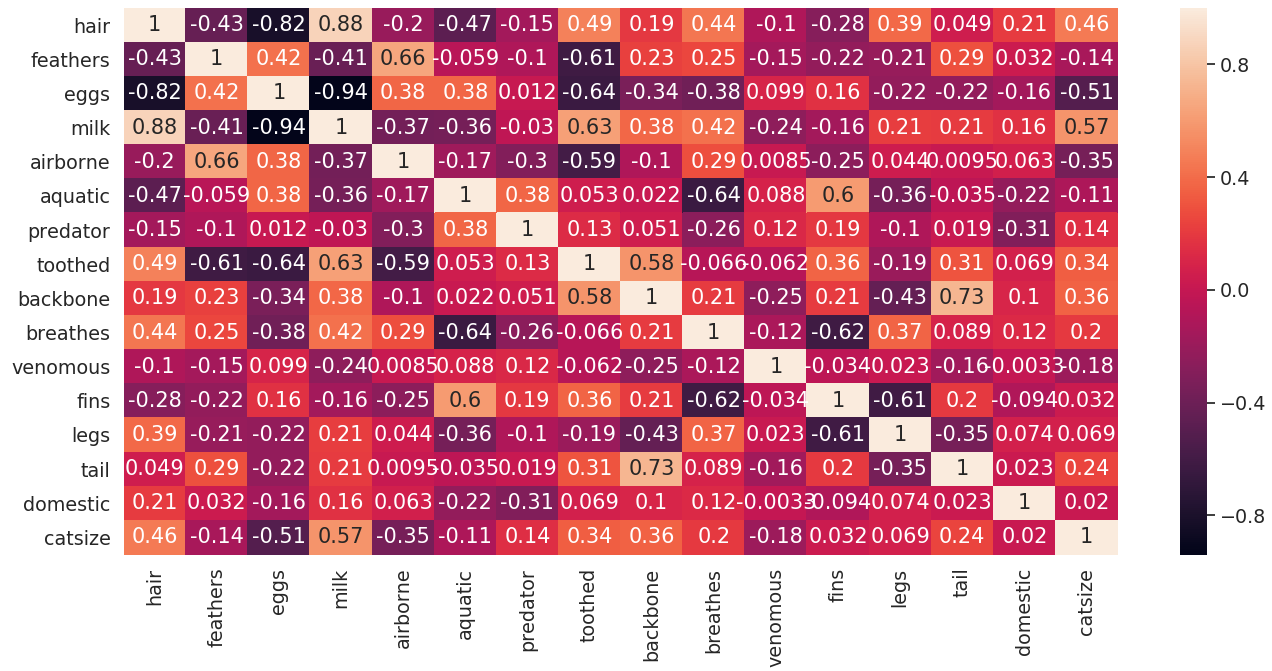
下面的代码用于通过制作元组列表来生成相关矩阵的3d图,其中元组包含按动物名称顺序排列的坐标和相关值。
上述解释的伪代码:
# PseudoCode
tuple -> (position_in_dataframe(feature1),
position_in_dataframe(feature2),
correlation(feature1, feature2))
用于生成相关矩阵的3d图的代码:
from matplotlib import cm
# generating correlation data
df = zoo_data.corr()
df.index = range(0, len(df))
df.rename(columns = dict(zip(df.columns, df.index)), inplace = True)
df = df.astype(object)
''' Generating coordinates with
corresponding correlation values '''
for i in range(0, len(df)):
for j in range(0, len(df)):
if i != j:
df.iloc[i, j] = (i, j, df.iloc[i, j])
else :
df.iloc[i, j] = (i, j, 0)
df_list = []
# flattening dataframe values
for sub_list in df.values:
df_list.extend(sub_list)
# converting list of tuples into trivariate dataframe
plot_df = pd.DataFrame(df_list)
fig = plt.figure()
ax = Axes3D(fig)
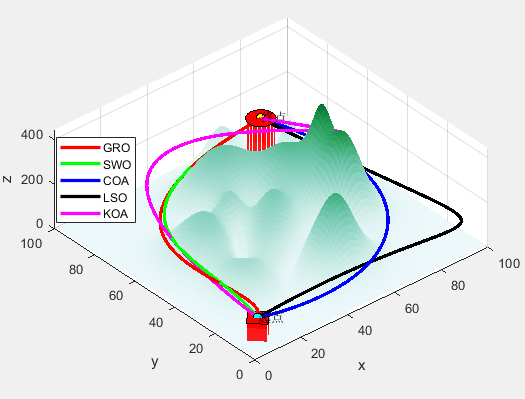
# plotting 3D trisurface plot
ax.plot_trisurf(plot_df[0], plot_df[1], plot_df[2],
cmap = cm.jet, linewidth = 0.2)
plt.show()
输出
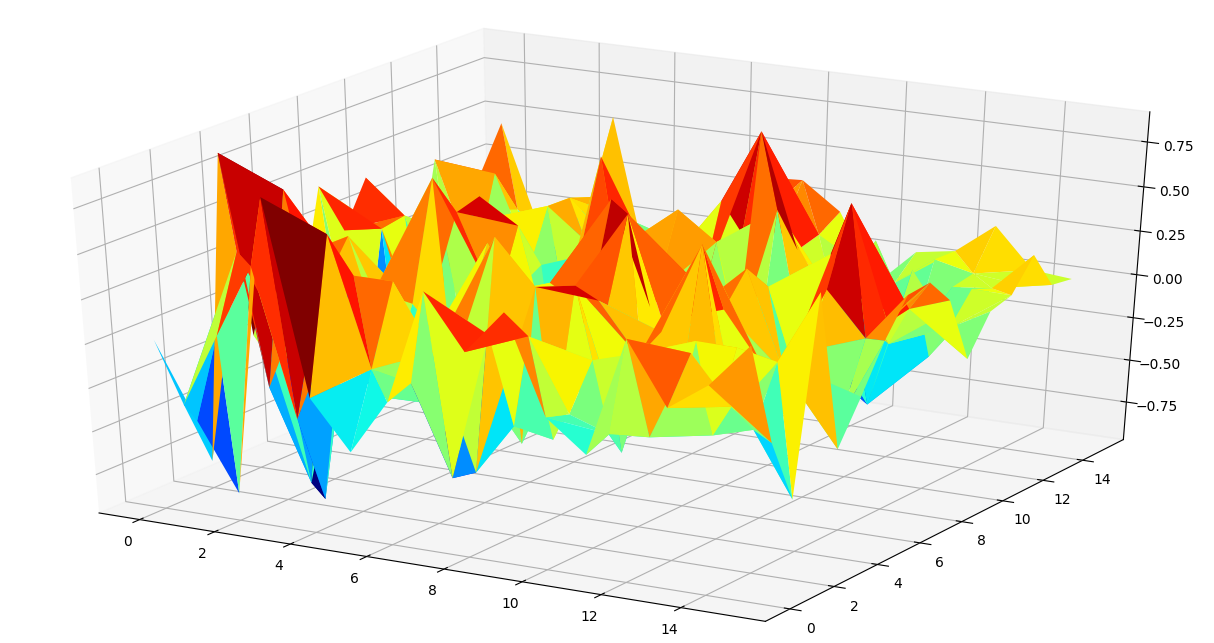
使用热图和3d图,我们可以对如何选择用于执行聚类分析的较小特征集进行一些推断。通常,具有极端相关值的特征对具有很高的解释力,可以用于进一步的分析。
在这种情况下,查看两个图,我们得到了7个特征的合理列表:[“milk”, “eggs”, “hair”, “toothed”, “feathers”, “breathes”, “aquatic”]
再次对子集特征集运行聚类分析,我们可以生成散点图,更好地推断如何在不同的群体中传播不同的动物。
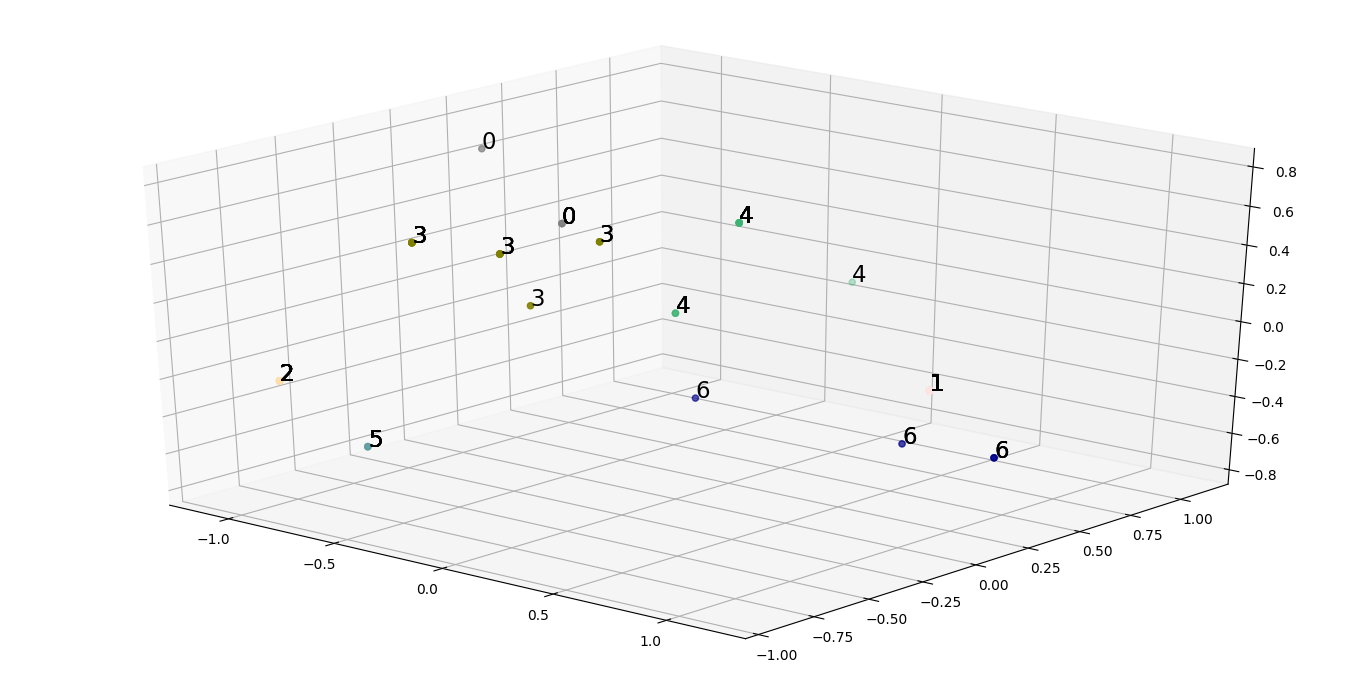
我们观察到减小的总inertia为14.479670329670329,这确实比初始inertia小得多。