一、背景
毕达哥拉斯的“万物皆数”哲学观点表达了一个理念,即宇宙万物都可以通过数学语言来描述,数是万物的本原。
勾股定理就是毕达哥拉斯提出,因此在西方勾股定理也被叫做毕达哥拉斯定理。
工科类的专业,越到后面越感觉到数学的重要性,无论是控制,计算机还是机器人专业,都需要很好的数学功底。
最近在做DMP相关的内容时,需要求解二阶微分方程,无奈早已把学的还给老师,可惜当时高数白考九十多分。但很感谢当时的高数老师于朝霞教授,讲课讲的真好,所以重新翻看高等数学第六版同济大学编著的微分方程章节时,很快捡起来之前学到的内容。
现在有了matlab,不需要自己手算了,下面记录一下使用matlab求解二阶微分方程的过程。
Matlab版本:2023a
二、Matlab求解二阶常系数微分方程
1、问题描述
二阶常系数微分方程:
y
¨
+
10
y
˙
+
25
y
=
250
(1)
\begin{aligned} \ddot y+10\dot y+25y=250 \\ \end{aligned}\tag{1}
y¨+10y˙+25y=250(1)
二阶微分方程如果没有初始条件,其通解会含有两个任意常数,所以不能完全反应某一客观实物的规律。
这里设置初始条件为:
y
(
0
)
=
15
,
y
˙
(
0
)
=
0
(2)
\begin{aligned} y(0)=15, &&\dot y(0)=0 \\ \end{aligned}\tag{2}
y(0)=15,y˙(0)=0(2)
2、matlab求解微分方程,并绘制解的曲线
clear; close all; clc;
% 定义符号变量
syms x y(x);
% 定义二阶微分方程
eqn = diff(y, x, 2) + 10*diff(y, x) + 25*y == 250;
% 设置初始条件
initial_condition1 = y(0) == 0; % 初始值 y(0) = 0
initial_condition2 = subs(diff(y), 0) == 0; % 初始导数值 y'(0) = 0
% 求解微分方程
sol = dsolve(eqn, [initial_condition1, initial_condition2]);
% 显示解
disp('解:');
disp(sol);
% 将解转换为函数句柄
ySol = matlabFunction(sol);
% 定义 x 范围
x = linspace(0, 5, 100); % 这里的范围可以根据需要调整
% 计算对应的 y 值
y = ySol(x);
% 绘制曲线图
figure;
a1 = subplot( 1, 1, 1 );
hold( a1, 'on' );
plot(a1, x, y, 'linewidth', 3, 'color', [0.0000, 0.4470, 0.7410] );
xlabel('x');
ylabel('y');
title('二阶微分方程的解曲线');
scatter( 0, ySol(0), 'filled', 'linewidth', 3, 'markerfacecolor', 'y', 'markeredgecolor', 'k' );
grid on;
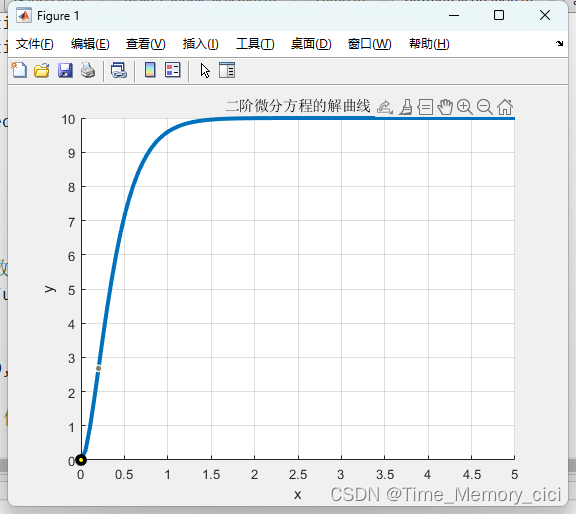
3、matlab求解加速度函数,并绘制解的曲线
经过步骤2,其实我们得到的是位置和速度的关系,即解为:
y
=
−
10
e
−
5
x
−
50
x
e
−
5
x
+
10
(2)
\begin{aligned} y=-10e^{-5x}-50xe^{-5x}+10 \\ \end{aligned}\tag{2}
y=−10e−5x−50xe−5x+10(2)
有时我们还需要观察加速度和时间的关系。
因此对公式(2)求二阶导,得到加速度:
y
¨
=
250
e
−
5
x
−
1250
x
e
−
5
x
(2)
\begin{aligned} \ddot y=250e^{-5x}-1250xe^{-5x} \\ \end{aligned}\tag{2}
y¨=250e−5x−1250xe−5x(2)
matlab里求解加速度与时间的关系,及画出曲线图:
clear; close all; clc;
% 定义符号变量
syms x;
% 定义函数
y = 10 - 50*x*exp(-5*x) - 10*exp(-5*x);
% 计算二阶导数
second_derivative = diff(y, x, 2);
% 显示解
disp('二阶导:');
disp(second_derivative);
% 将二阶导数转换为函数句柄
second_derivative_func = matlabFunction(second_derivative);
% 定义 x 范围
x_values = linspace(0, 5, 100); % 这里的范围可以根据需要调整
% 计算对应的二阶导数值
y_second_derivative = second_derivative_func(x_values);
% 绘制二阶导数曲线图
figure;
plot(x_values, y_second_derivative);
xlabel('x');
ylabel('y的二阶导数');
title('y=5*exp(-5*x) + 25*x*exp(-5*x) + 10 的二阶导数曲线');
grid on;









![[BJDCTF2020]Easy MD5 1](https://img-blog.csdnimg.cn/img_convert/08de61a0be78eedabffaa97ad4b3f09f.png)