多数元素
- 题解1 哈希表
- 题解2 Boyer-Moore 投票算法
给定一个大小为
n 的数组
nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于
⌊
n
/
2
⌋
⌊ n/2 ⌋
⌊n/2⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入:nums = [3,2,3]
输出:3
示例 2:
输入:nums = [2,2,1,1,1,2,2]
输出:2
提示:
n == nums.length- 1 <=
n<= 5 ∗ 1 0 4 5 * 10^4 5∗104 -
−
1
0
9
-10^9
−109 <=
nums[i]<= 1 0 9 10^9 109
进阶:尝试设计时间复杂度为 O ( n ) O(n) O(n)、空间复杂度为 O ( 1 ) O(1) O(1) 的算法解决此问题。
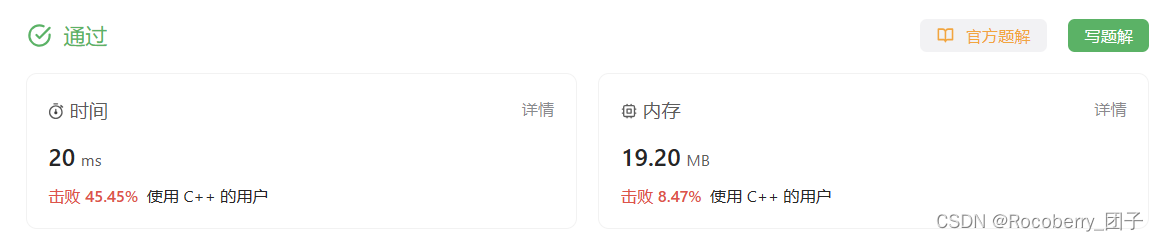
题解1 哈希表
class Solution {
public:
int majorityElement(vector<int>& nums) {
unordered_map<int, int> nmap;
for(int i = 0; i < nums.size(); i++){
nmap[nums[i]] ++;
if(nmap[nums[i]] > nums.size()/2)
return nums[i];
}
return nums[0];
}
};
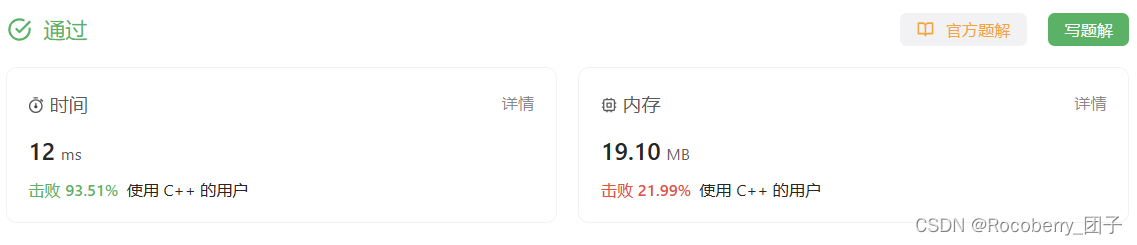
题解2 Boyer-Moore 投票算法
class Solution {
public:
int majorityElement(vector<int>& nums) {
int target = nums[0];
// 到当前的这一步遍历为止,众数出现的次数比非众数多出了多少次
int count = 0;
for(int i = 0; i < nums.size(); i++){
if(! count){
// 当前目标众数
target = nums[i];
count = 1;
// 是 count++
} else if(nums[i] == target){
count ++;
} else{
// 不是 count--,减到0换众数
count --;
}
}
return target;
}
};




![用友NC Cloud accept.jsp接口任意文件上传漏洞复现 [附POC]](https://img-blog.csdnimg.cn/bee64cf481f64a7e937200eaf7e2e74f.png)