目录

多彩的树

题目描述 

输入描述:

输出描述:

输入

输出

思路解析：

代码实现：

---

多彩的树

时间限制：C/C++ 5秒，其他语言10秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld

题目描述 

有一棵树包含 N 个节点，节点编号从 1 到 N。节点总共有 K 种颜色，颜色编号从 1 到 K。第 i 个节点的颜色为 Ai。
Fi 表示恰好包含 i 种颜色的路径数量。请计算：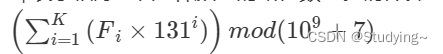

输入描述:

第一行输入两个正整数 N 和 K，N 表示节点个数，K 表示颜色种类数量。
第二行输入 N 个正整数，A1, A2, A3, ... ..., AN，Ai 表示第 i 个节点的颜色。

接下来 N - 1 行，第 i 行输入两个正整数 Ui 和 Vi，表示节点 Ui 和节点 Vi 之间存在一条无向边，数据保证这 N-1 条边连通了 N 个节点。

1 ≤ N ≤ 50000.
1 ≤ K ≤ 10.
1 ≤ Ai ≤ K.

输出描述:

输出一个整数表示答案。

示例1

输入

复制

5 3
1 2 1 2 3
4 2
1 3
2 1
2 5

输出

复制

4600065

思路解析：

状压dp + 容斥原理

dp[i] 表示在状态i下·的路径树， 状态i用二进制表示，i==10010，表示使用了颜色2和5，因为这里考虑已经使用了那些颜色比考虑现在的使用的颜色数量更任意统计，并且状态更加明确方便状态转移。

cnt 表示在状态10010下，在某个位置有多少个颜色2和5的节点相邻。cnt + (cnt) * (cnt - 1) / 2则表示当前状态下可能的路径方案总数。

dp[i] = (dp[i] + cnt + (cnt) * (cnt - 1) / 2) % mod;

因为可能有可能是 2 2 2 2 5 5 5.这样简单的cnt + (cnt) * (cnt - 1) / 2计算可能会导致计算有误，所以要排除非法答案。即状态为 00010和状态10000的情况。

if ((j & i) == j){
// System.out.println(i + " " + j);
dp[i] = (dp[i] - dp[j] + mod) % mod;
}

代码实现：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
import java.util.Arrays;
import java.util.Scanner;
import java.util.Vector;

/**
 * @ProjectName: study3
 * @FileName: Ex35
 * @author:HWJ
 * @Data: 2023/11/10 11:45
 */
public class Ex35 {
    static int mod = 1000000007;
    static long[] dp;
    static long cnt;
    static Vector<Vector<Integer>> g;
    static int[] vis;
    static int[] col;

    public static void main(String[] args) throws IOException {
        Scanner input = new Scanner(System.in);
        StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
        in.nextToken();
        int n = (int) in.nval;
        in.nextToken();
        int m = (int) in.nval;
        int[] pow = new int[m + 1];
        for (int i = 0; i < m; i++) {
            pow[i + 1] = (int) quick(i + 1);
        }
        dp = new long[1 << m]; // 用颜色做状态转移。
        vis = new int[n + 1];
        g = new Vector<>();
        col = new int[n + 1];
        for (int i = 0; i < n; i++) {
            in.nextToken();
            col[i + 1] = (int) in.nval;
        }
        for (int i = 0; i < n + 1; i++) {
            g.add(new Vector<>());
        }
        for (int i = 0; i < n - 1; i++) {
            in.nextToken();
            int x = (int) in.nval;
            in.nextToken();
            int y = (int) in.nval;
            g.get(x).add(y);
            g.get(y).add(x);
        }
        for (int i = 1; i < 1 << m; i++) {
            Arrays.fill(vis, 0);
            for (int j = 1; j <= n; j++) {
                cnt = 0;
                if ((i & (1 << (col[j] - 1))) == 0 || vis[j] == 1) continue;
                dfs(j, 0, i);
                dp[i] = (dp[i] + cnt + (cnt) * (cnt - 1) / 2) % mod;
//                System.out.println(i + " " + (j - 1) + " " + cnt);
            }
            for (int j = i - 1; j > 0; j--) {
                if ((j & i) == j){
//                    System.out.println(i + " " + j);
                    dp[i] = (dp[i] - dp[j] + mod) % mod;
                }

            }
        }
        long ans = 0;
        for (int i = 1; i <1 << m; i++) {
            int t = 0;
            int k = i;
            System.out.println(dp[i]);
            while (k > 0){
                if ((k & 1) != 0) t++;
                k >>= 1;
            }
            ans = (ans + (long) pow[t] * dp[i]) % mod;
        }
        System.out.println(ans);
    }

    public static void dfs(int x, int fa, int st){
        cnt++;
        vis[x] = 1;
        for (int i = 0; i < g.get(x).size(); i++) {
            int y = g.get(x).get(i);
            if (y == fa || (st & (1 << (col[y] - 1))) == 0 || vis[y] == 1) continue;
            dfs(y, x, st);
        }
    }

    public static long quick(int p) {
        long ans = 1;
        long x = 131;
        for (; p > 0; p >>= 1, x = (x * x) % mod) {
            if ((p & 1) == 1) ans = (ans * x) % mod;
        }
        return ans;
    }
}