生物神经网络以人工神经网络的形式建模, 其中人工神经元模拟生物神经元的功能。人工神经元如下图所示:
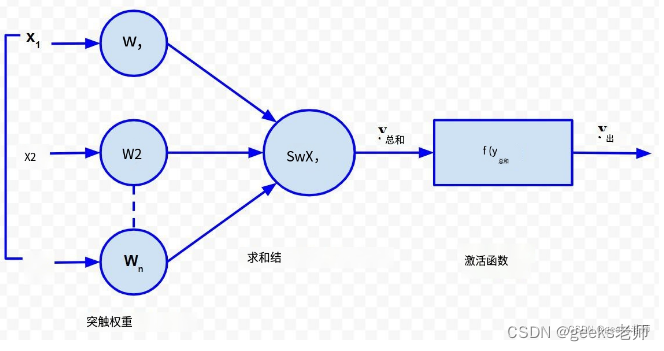
人工神经元的结构
每个神经元由三个主要部分组成:
- 一组“i”个突触,其权重为 w i。信号 x i形成具有权重 w i的第 i 个突触的输入。任何权重的值都可以是正值或负值。正权重具有非凡的效果,而负权重对求和点的输出具有抑制作用。
- 输入信号的求和点由相应的突触权重加权。因为它是加权输入信号的线性组合器或加法器,所以求和点的输出可以表示如下:

- 阈值激活函数(或简称激活函数,也称为挤压函数)仅当超过特定阈值的输入信号作为输入时才会产生输出信号。它的行为类似于生物神经元,仅当总输入信号满足发射阈值时才传输信号。
激活函数的类型:
有不同类型的激活函数。下面列出了最常用的激活函数:
A.恒等函数:恒等函数用作输入层的激活函数。它是一个线性函数,其形式为
![]()
显然,输出与输入保持相同。
B. 阈值/步长函数:是常用的激活函数。如图所示,当输入的输出为 0 或正值时,它给出1 。如果输入为负,则输出为 0。用数学的方式表达出来,
![]()
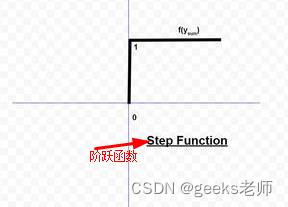
阈值函数几乎类似于阶跃函数,唯一的区别是
![]()
用作阈值而不是 。用数学的方式表达,
![]()
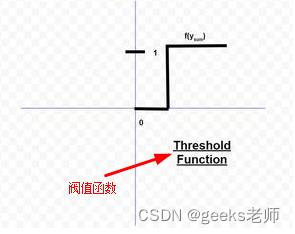
C. ReLU(修正线性单元)函数:它是卷积神经网络和深度学习领域最常用的激活函数。它的形式如下:
![]()
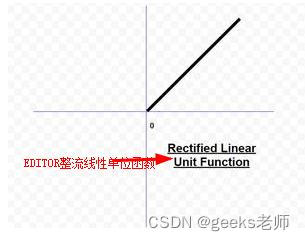
这意味着当 x 小于零时 f(x) 为零,当 x 大于或等于 0 时 f(x) 等于 x。该函数是可微的,除了在单点 x = 0 处。从这个意义上说,ReLU 的导数实际上是次导数。
D. Sigmoid 函数:它是迄今为止神经网络中最常用的激活函数。对 sigmoid 函数的需求源于这样一个事实:许多学习算法要求激活函数是可微的,因此是连续的。sigmoid 函数有两种类型:
1.二元Sigmoid函数
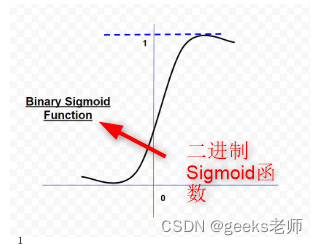
二元 sigmoid 函数的形式为:
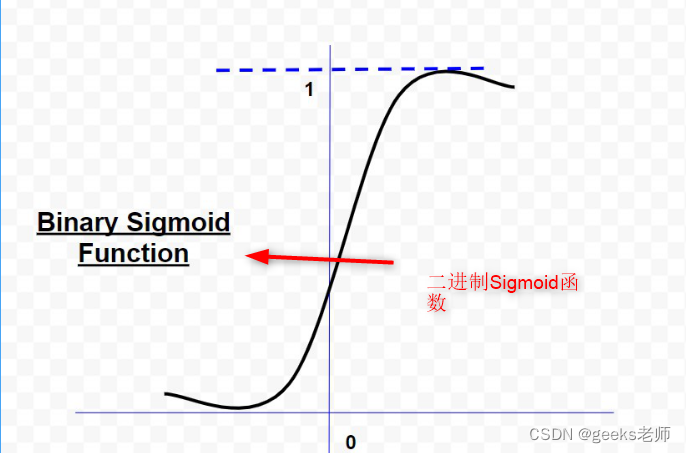
,其中k = 陡度或斜率参数,通过改变 k 的值,可以获得不同斜率的 sigmoid 函数。它的范围是(0,1)。原点的斜率是k/4。当k的值变得非常大时,sigmoid函数就变成了阈值函数。
2. 双极 Sigmoid 函数
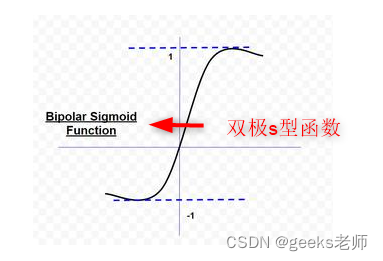
双极 sigmoid 函数的形式为
![]()
sigmoid 函数的值范围可以根据应用而变化。然而,最常用的范围是(-1,+1)。
E. 双曲正切函数:它本质上是双极的。它是一种被广泛采用的激活函数,用于一种称为反向传播网络的特殊类型的神经网络。双曲正切函数的形式为
![]()
该函数类似于双极 sigmoid 函数。




![【洛谷 P1012】[NOIP1998 提高组] 拼数 题解(贪心算法+字典序排序)](https://img-blog.csdnimg.cn/bee5ba42cb4d43aabdcd59dcb9766e44.jpeg)
![Verilog刷题[hdlbits] :Always nolatches](https://img-blog.csdnimg.cn/1671f14bd9264b2cb89d69e23fb7e0b3.png)