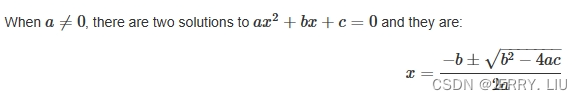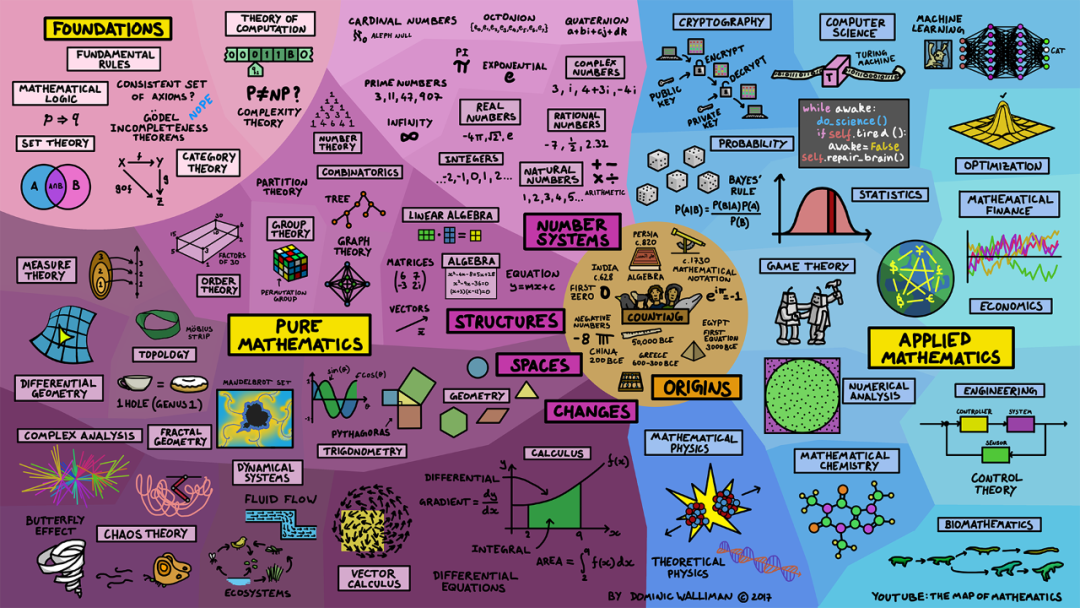
我们在学校学习的数学可能也只是数学领域的冰山一角,作为庞大而多样的学科,我今天将通过一张数学地图带你尽览数学分支。
本数学地图对应的视频讲解地址如下:
https://www.youtube.com/watch?v=OmJ-4B-mS-Y
另外,由于图片较大,建议下载到本地查看,关注微信公众号:人工智能大讲堂,后台回复mmap获取下载链接。
一.数学起源于计数
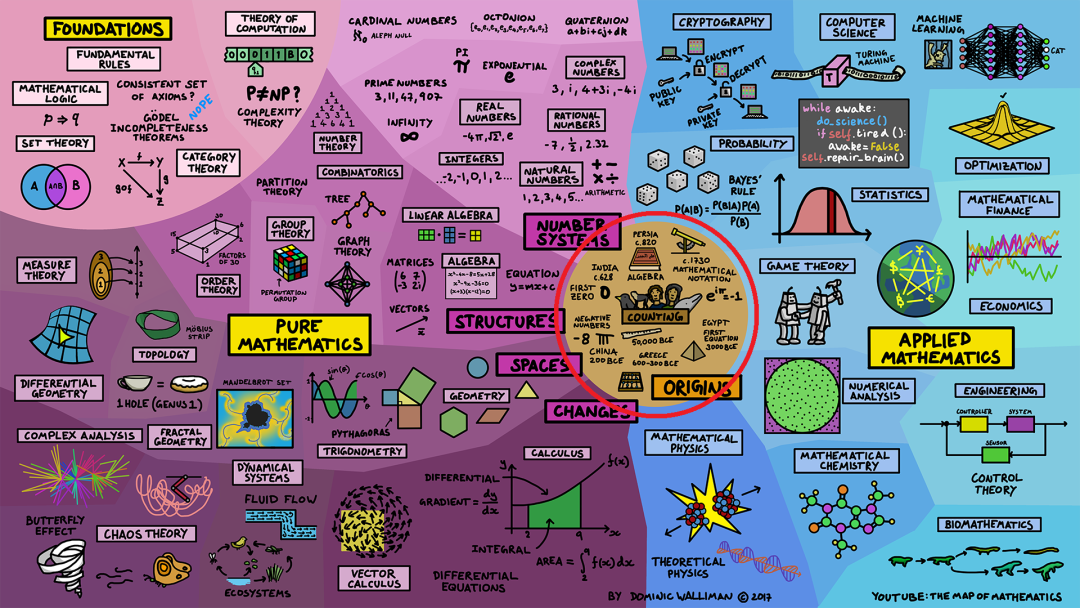
1.1数学的起源
人类计数(count)可以追溯到史前时代,人们在骨头上刻画记号。随着时间的推移,数学发生了几次创新,埃及人首次提出了方程,古希腊人在几何学和数理数学等许多领域取得了重大进展,负数在中国发明,零作为一个数字最早在印度使用。
这个时期我们称之为古代数学(约前3000年-约前300年),这里给大家一个时间上的参照,古希腊人毕达哥拉斯提出勾股定理时我国正处于春秋战国时期。
然后,在伊斯兰黄金时代,波斯数学家取得了进一步的发展,第一本代数学著作被写成。这个时期也被称为中世纪数学(约500年-1400年),而此时中国正在跨越唐宋元明等朝代。
然后,在文艺复兴时期,数学与科学一起蓬勃发展。解析几何、微积分的创立。出现了对数、概率论等分支。这个时期我们也称为近代数学(17世纪-19世纪),而此时的中国正处于没落的大清王朝。
而我们主要关注现代数学(20世纪至今)。
二.数学的两大分支
现代数学可以大致分为两个领域,左侧的纯数学(Pure Mathematics)和右侧的应用数学(Appiled Mathematics)。
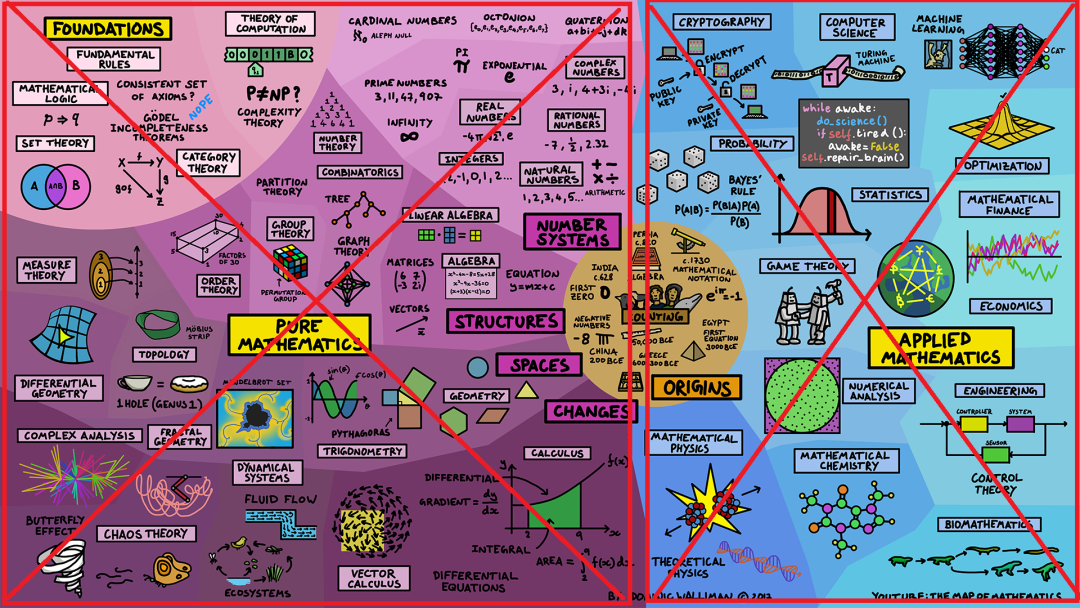
纯数学研究数学本身,而应用数学则是为了解决现实世界的问题。但两者之间并非泾渭分明。很多科学家在其所在的领域科研时发现一些古老的纯数学理论正是他们解决现实世界问题所需要的,即使时间跨度几个世纪,抽象的东西最终变得非常有用。
好了,让我们开始进入正题,纯数学由几个部分组成。
纯数学:数字系统(Number Systems)
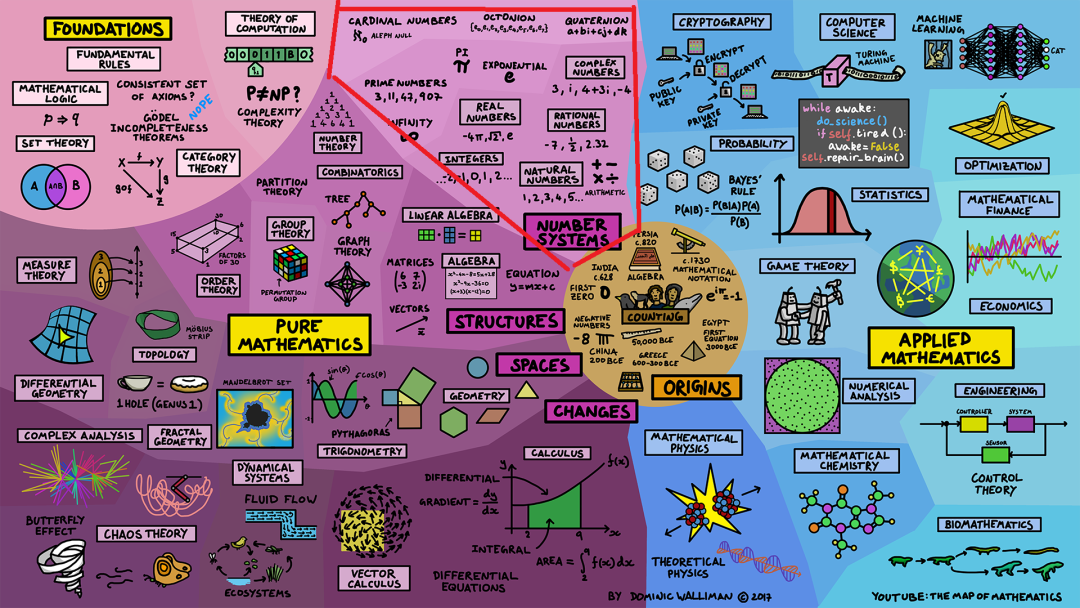
数字的研究从自然数(Natural Numbers)开始,以及你可以用它们做什么,例如算术运算(Arithmetic),然后研究其他类型的数字,如整数(Integer)(包括负数)、有理数(Rational Numbers)(如分数)、实数(Real Numbers)(包括像π这样的无限小数)以及复数(Complex Numbers)等等。以及一些具有有趣的特性的数字,如素数、π或指数。
纯数学:结构(Structures)
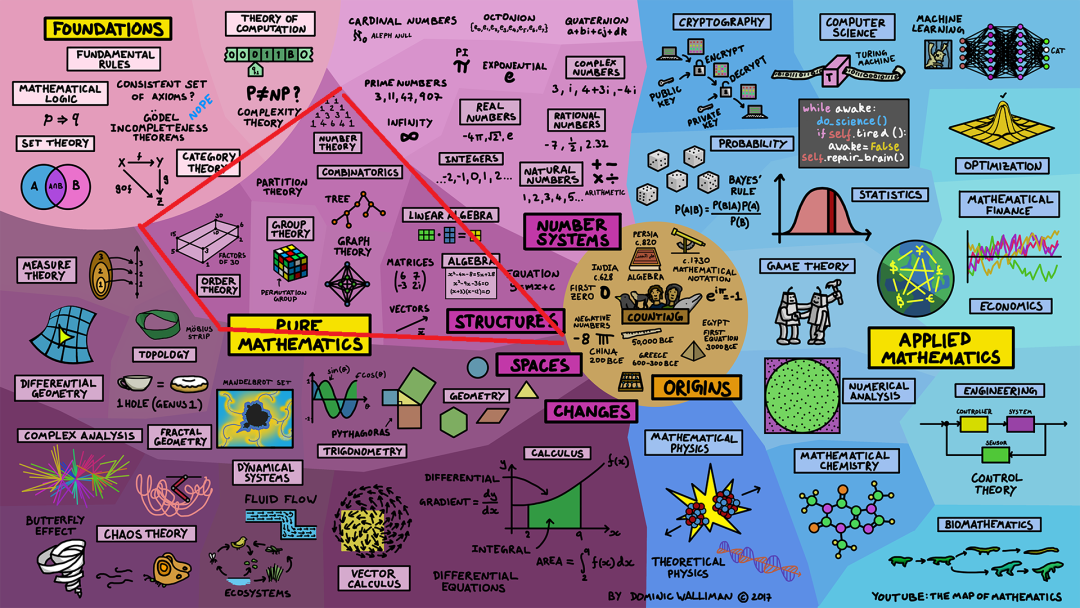
研究结构的学科是从将数字放入变量形式的方程式开始,代数(Algebra)包含了处理这些方程式的规则。在代数中,你还会找到向量(Vector)和矩阵(Matrices),它们之间的关系规则被捕捉在线性代数(Linear Algebra)中。
数论(Number Theory)研究数字系统中数字的特性,例如素数的性质。
组合学(Combinatorics)研究特定结构的性质,如树(Tree)、图(Graph)以及由离散块组成的其他事物。
群论(Group Theory)研究相互关联的对象,例如魔方是置换群的一个例子。
序理论(order theory)研究如何按照一定的规则排列对象。自然数就是有序对象的一个例子。
纯数学:空间(Space)与形状(Shape)
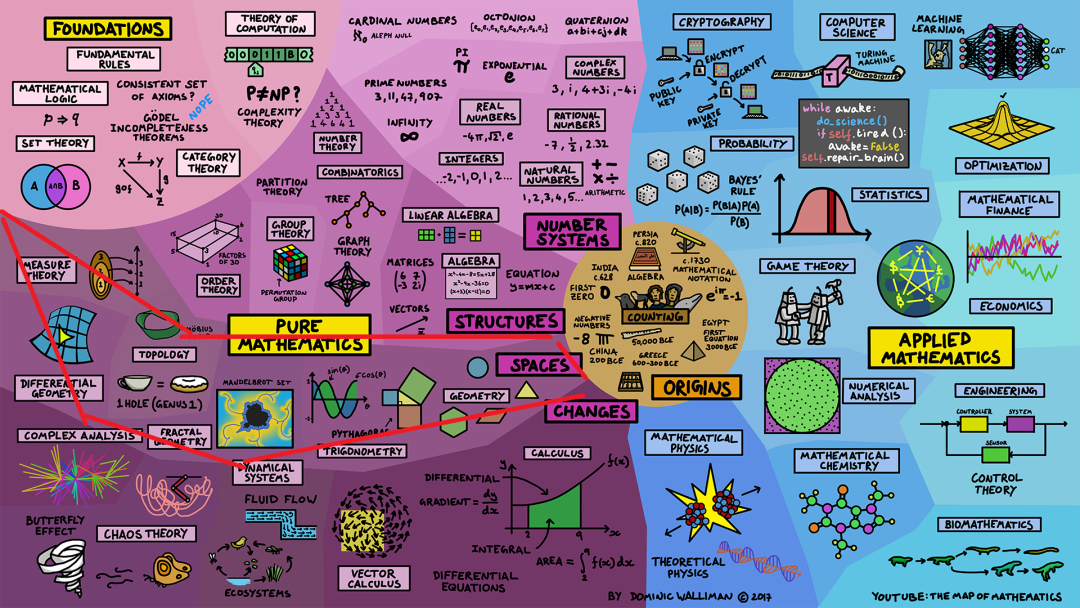
纯数学的另一个部分研究形状(Shape)及其在空间(Space)中的行为。
起源于几何学(Geometry),其中包括与三角学(trigonometry)密切相关的毕达哥拉斯学派,如果说毕达哥拉斯定理你不知道,那换个称呼勾股定理你一定很熟悉。
还有一些有趣的东西,例如分形几何(Fractal Geometry),它是一种数学模式,具有尺度不变性,这意味着你可以无限缩放它们,它们看起来总是差不多的。
拓扑学(Topology)研究允许连续变形但不允许撕裂或粘合的空间的不同属性。例如,咖啡杯和甜甜圈在拓扑上是相同的。
测度论(Measure Theory)是一种给空间或集合分配值的方法,将数字和空间联系在一起。
最后,微分几何(Differential Geometry)研究曲面上形状的性质。例如,在曲面上,三角形的角度是不同的。
纯数学:变化(changes)
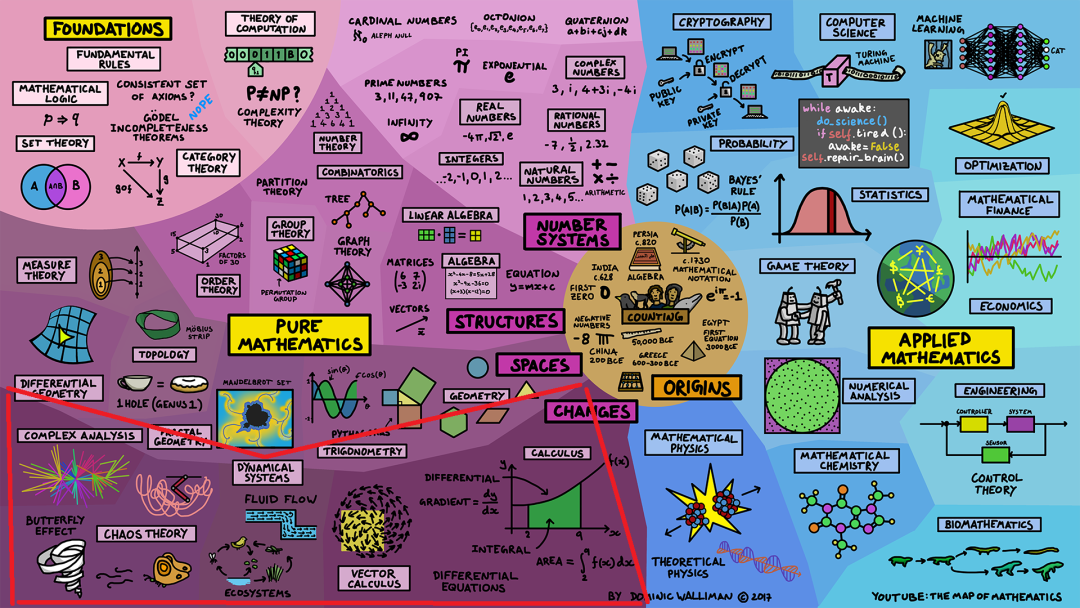
接下来我们来到下一个部分,即变化(changes)。
研究变化的学科包括微积分(calculus),涉及到积分(integrals)和微分(differentials)。微积分研究函数所围成的面积或函数梯度(gradients)的行为。而矢量微积分(vector calculus)则研究同样的内容,但针对矢量进行分析。
在这里,我们还会涉及到一系列其他领域,如动态系统(dynamical systems),它研究随时间从一个状态演变到另一个状态的系统,例如流体流动(fluid flows)或具有反馈环路的生态系统(ecosystems)和混沌理论(chaos theory),它研究对初始条件非常敏感的动力系统。
最后,复分析(complex analysis)研究具有复数的函数的性质。
应用数学:百花齐放
我们将从物理学(physics)开始,它在某种程度上使用了左侧几乎所有的内容。数学和理论物理学(theoretical physics)之间有着非常密切的关系。
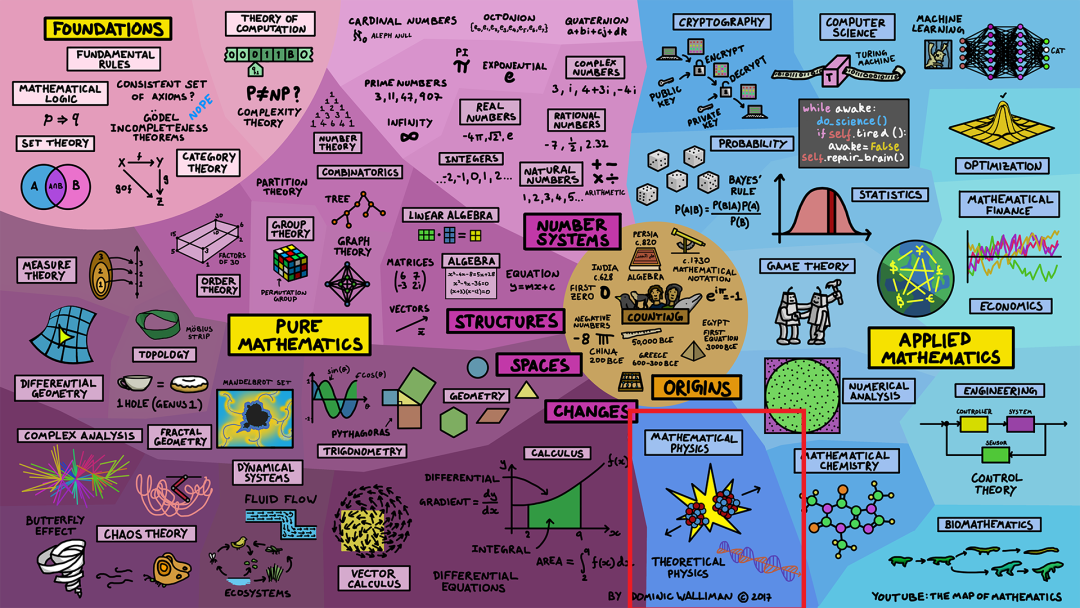
数学也在其他自然科学中得到应用,包括数学化学(mathematical chemistry)和生物数学(biomathematics),它们研究了从分子建模到进化生物学等各种内容。
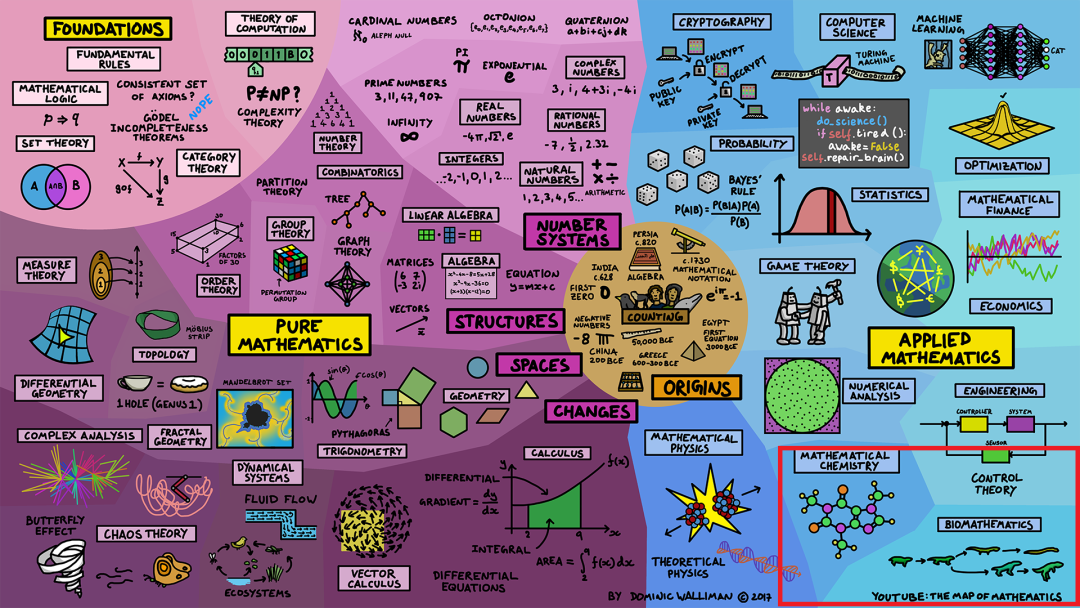
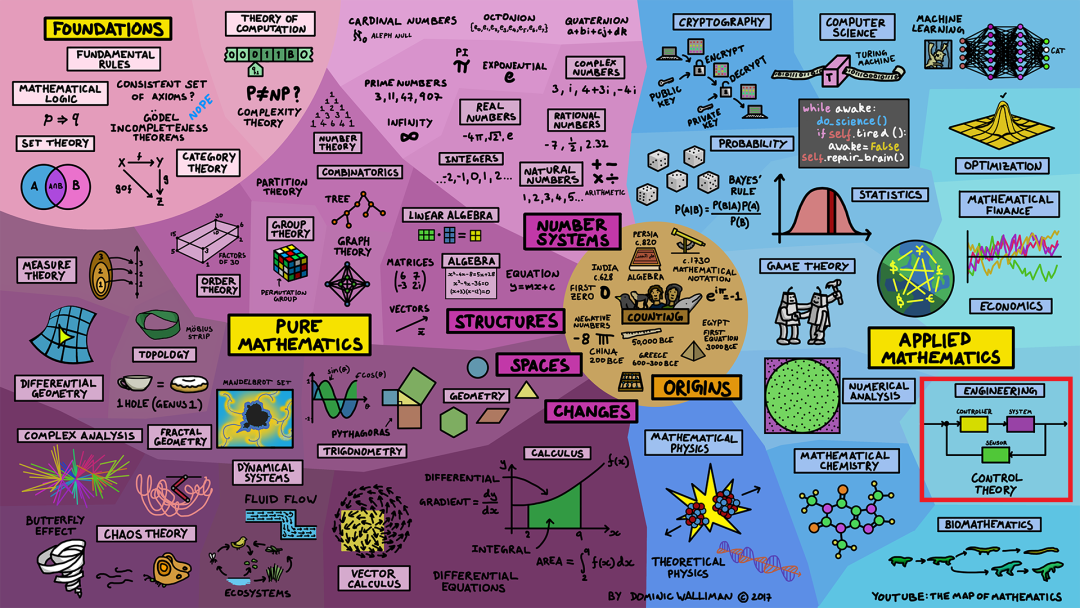
数学在工程学(engineering)中也被广泛应用。自从古埃及和巴比伦时代以来,建造事物就需要大量的数学知识。非常复杂的电气系统,例如飞机或电力网络,使用了动力系统中的控制理论(control theory)方法。
数值分析(numerical analysis)是一种数学工具,通常在数学变得过于复杂无法完全解决的情况下使用。因此,我们会使用许多简单的近似方法,并将它们组合在一起,以获得良好的近似答案。例如,如果你把一个圆放在一个正方形内,然后向它投掷飞镖,然后比较圆内和正方形部分的飞镖数量,你可以近似计算出圆周率的值。但在现实世界中,数值分析是在大型计算机上进行的。
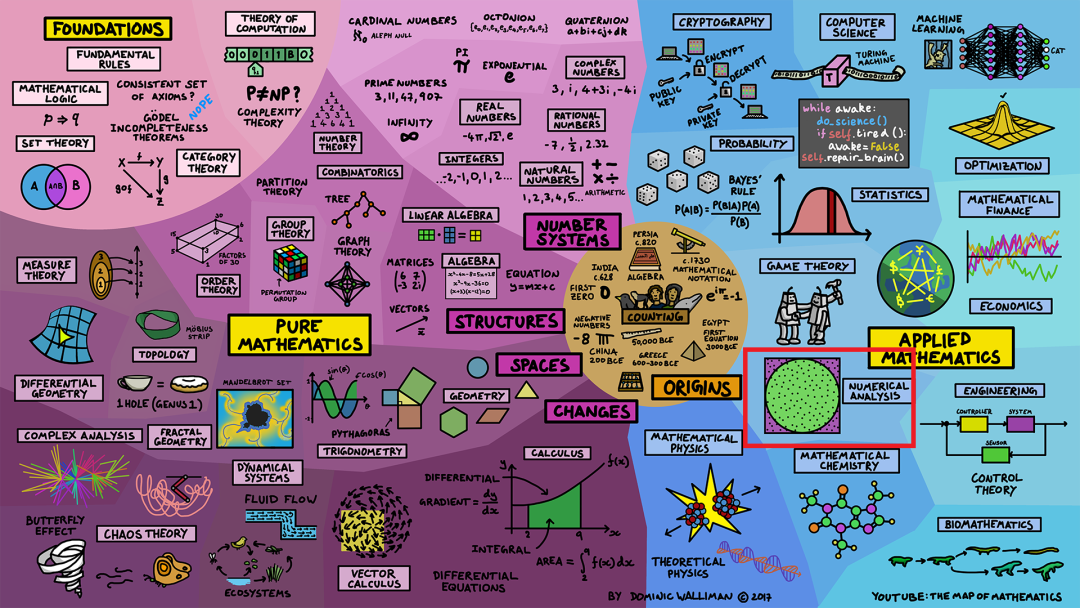
博弈论(game theory)研究在给定一组规则和理性玩家的情况下,最佳选择是什么,并且它在经济学(economics)中使用。
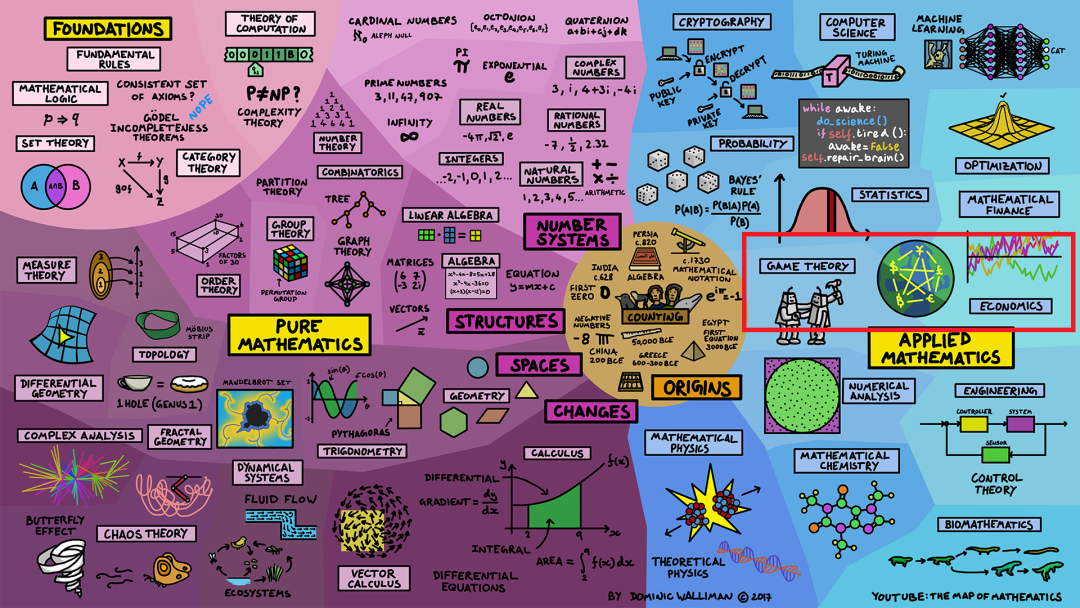
概率论(probability)是研究随机事件的学科,例如抛硬币、掷骰子或人类行为。
统计学(statistics)是研究大量随机过程或数据组织和分析的学科。
这显然与数学金融(mathematical finance)相关,您希望对金融系统建模并获得优势,以赢得丰厚的回报。
与回报相关的是优化(optimization),您试图在众多不同选项或约束条件中计算出最佳选择,通常将其视为寻找函数最高点或最低点。优化问题对我们人类来说是第二天性,我们经常进行这样的计算,试图在某种方式上获得最佳性价比或最大化幸福感。
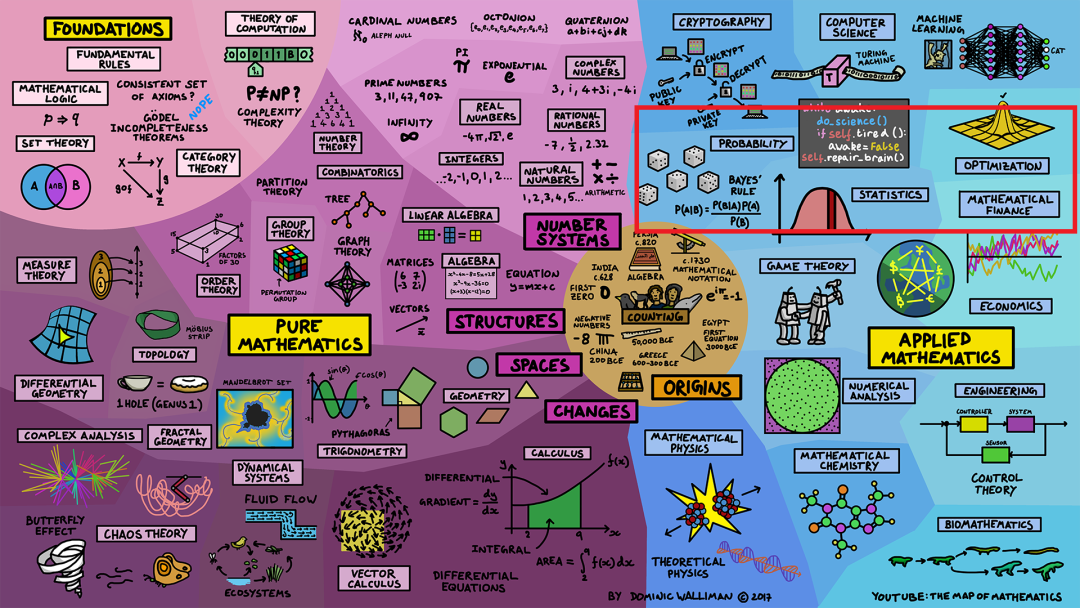
与纯数学密切相关的另一个领域是计算机科学(computer science)。计算机科学的规则实际上是从纯数学中推导出来的,这是一个在可编程计算机出现之前就被研究出来的例子。
机器学习(machine learning)是创建智能计算机系统的过程,它使用了线性代数、优化、动力系统和概率等数学领域的许多方法。
最后,密码学(cryptography)理论对计算非常重要,它使用了许多纯数学方法,如组合数学和数论。
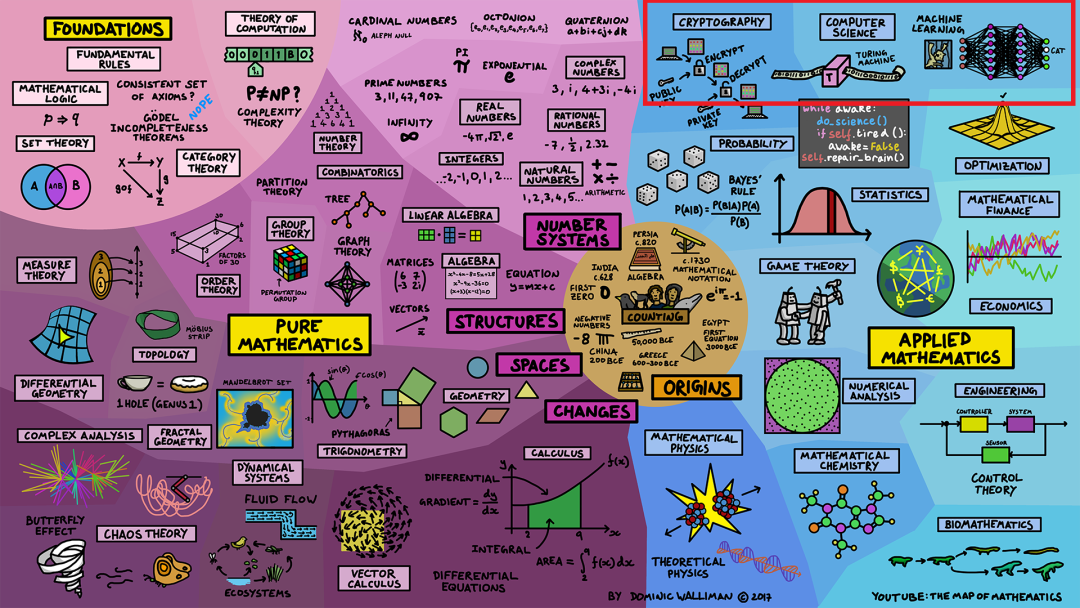
三.数学的基础
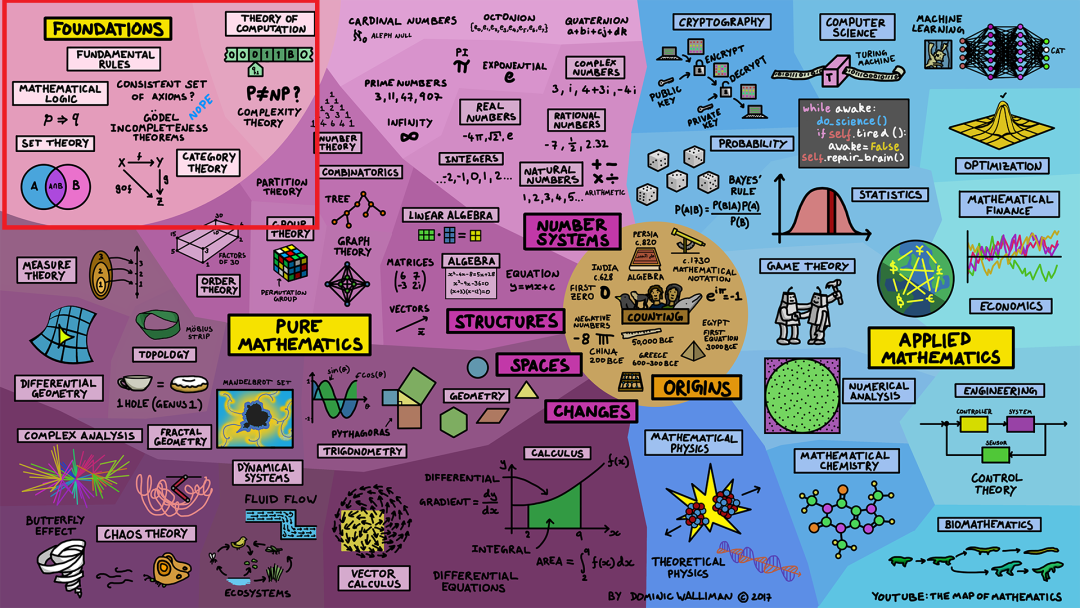
到这里我们已经讲了纯数学和应用数学的主要领域,但不能结束,还要看看数学的基础。
这个领域试图研究数学本身的属性,并询问数学规则的基础是什么。是否存在一个完整的基础规则集,称为公理,从中可以推导出所有的数学内容?我们能否证明这些规则与自身的一致性?数理逻辑、集合论和范畴论试图回答这些问题。在数理逻辑中,著名的结果是哥德尔的不完全性定理,对大多数人来说,这意味着数学没有一个完整而一致的公理集。这意味着数学在某种程度上是由我们人类所创造的,这有点奇怪,因为数学能够如此完美地解释宇宙中的许多事物,为什么人类创造出来的东西能够做到这一点,这是一个深奥的谜团。我们还有计算理论,它研究不同的计算模型以及它们在解决问题时的效率,其中包括复杂性理论,它研究什么是可计算的和不可计算的,以及需要多少内存和时间。对于大多数有趣的问题来说,所需的计算资源是巨大的。
这就是数学的地图。



![【洛谷 P1012】[NOIP1998 提高组] 拼数 题解(贪心算法+字典序排序)](https://img-blog.csdnimg.cn/bee5ba42cb4d43aabdcd59dcb9766e44.jpeg)
![Verilog刷题[hdlbits] :Always nolatches](https://img-blog.csdnimg.cn/1671f14bd9264b2cb89d69e23fb7e0b3.png)