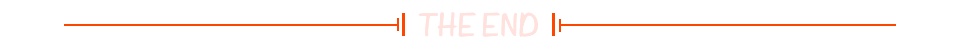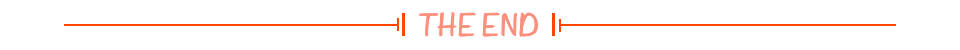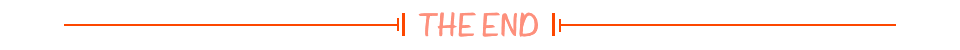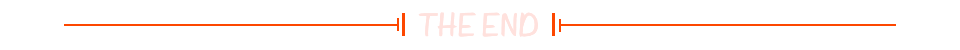1：背景与动机

        正如本系列之前的文章所述，统计学习理论为理解机器学习推理问题提供了一个概率框架。用数学术语来说，统计学习理论的基本目标可以表述为：

图片由作者提供

本文是统计学习理论系列的第 5 部分。前四件是：

• 第 1 部分：Hoeffding 不等式的推导与模拟
• 第 2 部分：贝叶斯分类器的最优性
• 第 3 部分：学习的 ML 估计器的收敛性和一致性
• 第 4 部分：有限函数类的一致性

在本系列的第 1 部分中，我们从第一原理推导了霍夫丁不等式，在第 2 部分中，我们证明了贝叶斯分类器的最优性，在第 3 部分中，我们开发了评估数据自适应机器学习采样估计器一致性的理论，在第4 部分中，我们推导了一致性有限大小函数类上的 ML 估计器的速率和泛化界限。在这篇文章中，我们将我们的理论扩展到无限大小函数类上的学习 ML 估计器，并利用破碎系数导出一致性率和泛化界限。

为了激发当前的兴趣问题，请考虑：

图片由作者提供

我们定义：

图片由作者提供

并回忆一下：

图片由作者提供

        但是，如果我们考虑无限大小的函数类而不是有限的函数类怎么办？比如所有线性模型的函​​数类？在这种情况下，我们还有一致性吗？

        在接下来的注释中，我们利用破碎系数推导了无限函数类上的 ML 估计器的不等式、比率和泛化界限。

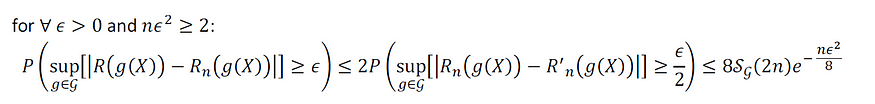
本文的目录如下：

        话虽如此，让我们开始吧。

2：破碎系数

2.1：破碎系数的定义

         我们想要测量无限函数类的容量。破碎系数是此类容量测量中最简单的。

让我们通过一些简单的玩具示例来了解破碎系数的示例。

2.2：玩具示例#1

2.3：玩具示例#2

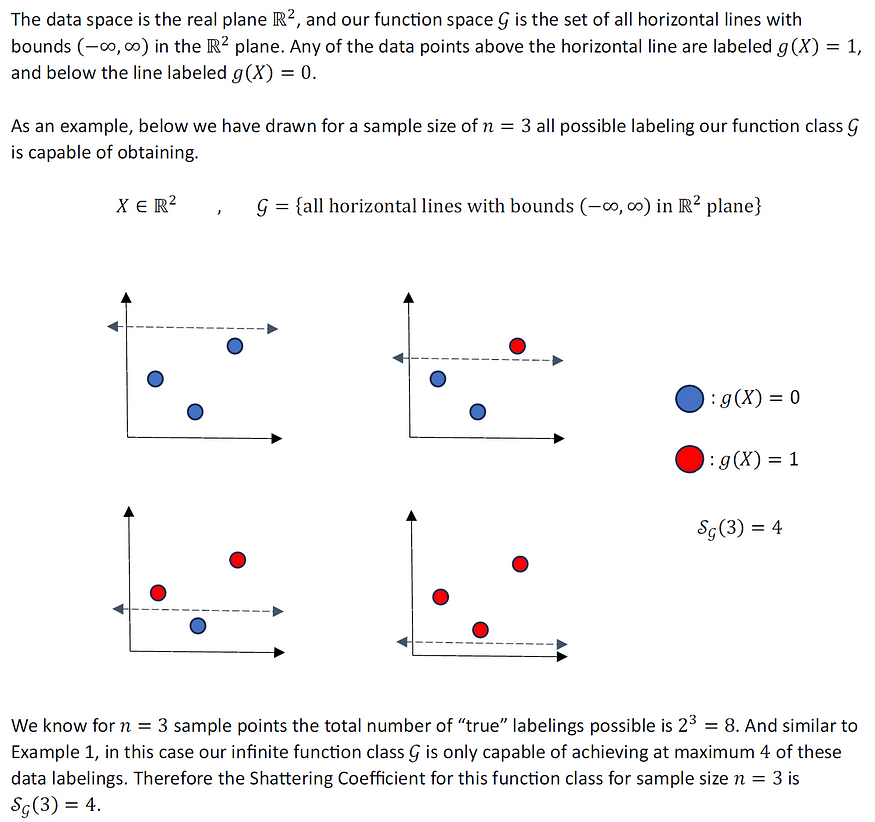
2.4：玩具示例#3

3：通过幽灵样本得出统计不平等

从本系列第 4 部分中的统计不平等开始：

我们将在本节中证明上述不等式右侧的进一步约束如下：

为了证明上述统计不等式，我们首先证明以下中间结果，稍后我们将利用：

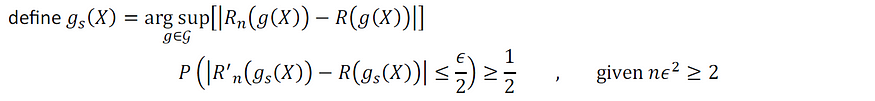
上述中间结果的证明如下：

我们现在准备证明：

上述不等式的证明如下：

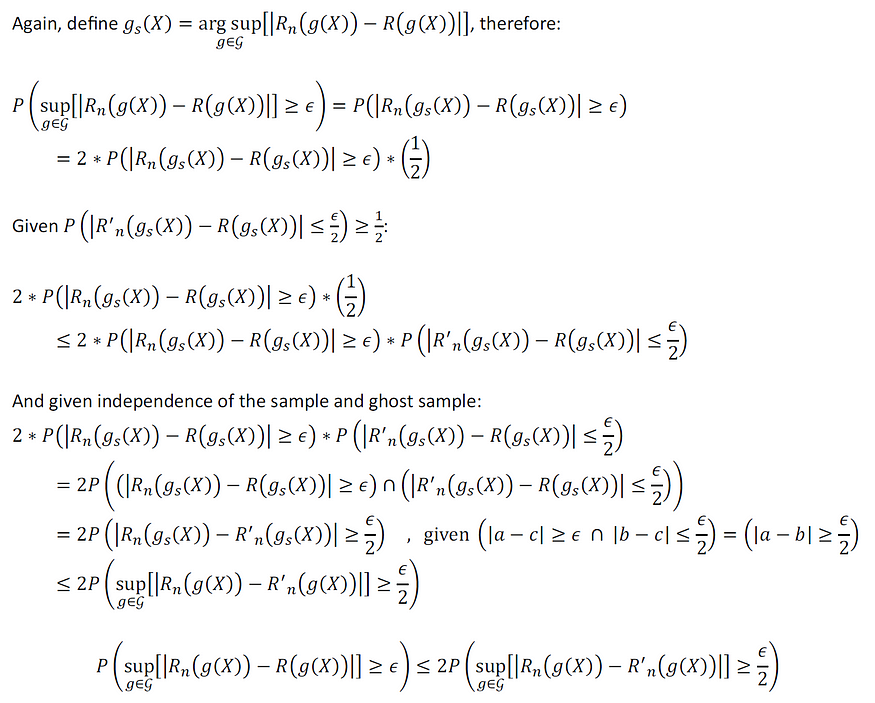
使用上面的统计不等式，在下一节中，我们利用破碎系数检查泛化界限和一致性率。

4：泛化界限和一致性率

根据上一节的结果，我们现在准备展示：

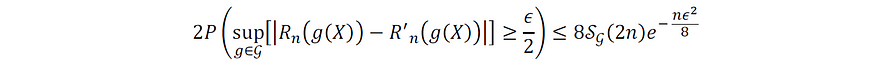
上述泛化界限的证明如下：

5：总结和结论

        请注意，虽然我们能够导出无限大小函数类上的 ML 估计器的泛化界限和一致性率，但本文中的方法存在一些缺点。主要是：

• 除了简单的玩具示例之外，破碎系数通常很难计算或计算。
• 破碎系数也是特定样本大小“ n ”的函数，这意味着我们需要知道该系数渐近增长的速度，以便将其用于本文中使用的目的。

        在本系列的后续第 6 部分中，我们将利用另一个工具来导出无限大小函数类的容量，即 Vapnik-Chervonenkis (VC) 维度。正如我们将在下一篇文章中看到的，对于某些用例，VC 维度比破碎系数更容易计算。与破碎系数不同，VC 维度不依赖于样本大小“ n ”。

        为了参考扎实的统计学习理论内容，我会推荐Larry Wasserman（卡内基梅隆大学统计和机器学习教授）的教科书“All of Statistics”和“All of Nonparametric Statistics”、斯坦福大学教师的“ Elements of Statistical Learning ”和“Statistical”弗拉基米尔·瓦普尼克（Vladimir Vapnik）的学习理论。

安德鲁·罗斯曼