3.1 什么是概率

概率亦称“或然率”，它反映随机事件出现的可能性大小，在现实生活中有着极其普遍的应用。

3.1.1 最简单的概率的例子

3.1.2 概率论与数理统计的关系

概率论与数理统计的关系可以概括为，概率论是数理统计的理论基础，数理统计是概率论 的一种应用。

3.2 搞懂大数定律与中心极限定理

3.2.1 大数定律想表达什么

1.大数定律是什么

最早的大数定律由伯努利在他的著作《推测术》 中提出并给出了证明。

大数定律告诉我们大量重复出现的随机事件中蕴含着某种必然的规律。保持试 验条件不变，多次地重复试验，随机事件出现的概率近似于它出现的频率。

大数定律有多种表达方式，例如切比雪夫大数定律、伯努利大数定律、辛钦(又译为欣钦) 大数定律等。

对一般人来说，大数定律非严格的表述是这样的:X1,...,Xn 是独立同分布随机变量序列，期

望为 u，且 ，则 收敛到 u。大数定律分为弱大数定律和强大数定律，如果说上述 收敛是指依概率收敛，那就是弱大数定律;如果说上述收敛是指几乎必然收敛，那就是强大数定律。大数定律是概率论甚至数学领域最直观的定律之一。

2.代码演示理解大数定律

3.2.2 中心极限定理想表达什么

1.中心极限定理是什么

中心极限定理告诉我们，当样本量足够大时，样本均值的分布围绕总体均值呈现正态分布。

2.代码演示理解中心极限定理

3.2.3 大数定律与中心极限定理的区别

大数定律表达的核心:随着样本容量的增加，样本均值将接近总体均值。

中心极限定理表达的核心:样本独立同分布的情况下，抽样样本均值围绕总体样本均值呈现 正态分布。

大数定律揭示了大量随机变量的平均结果，但没有涉及随机变量的分布问题。而中心极限定理说明在一定条件下大量独立随机变量的平均数是以正态分布为极限的。

3.3 理解概率统计中的重要分布

3.3.1 真正搞懂正态分布

1.正态分布是什么

以一维数据为例，正态分布的定义:若随机变量 X 服从一个数学期望为 μ、方差为 σ2 的正态分布，则可记为 N(μ,σ2)。其概率密度函数决定了正态分布的期望值 μ 的位置，其标准差 σ 决定了分布的幅度。μ = 0，σ = 1 的正态分布就是标准正态分布。

2.正态分布背后的原理是什么

正态分布背后的原理就是我们前文讲述的中心极限定理。中心极限定理还指出一个重要的结论:无论随机变量呈现出 什么分布，只要我们抽样次数足够多，抽取样本的均值就围绕总体的均值呈现正态分布。随着 抽取组数的增多，每次抽样的均值分布越来越趋近正态分布。

中心极限定理指出大量相互独立的随机变量的均值经适当标准化后依分布收敛于正态分布， 其中有 3 个要素:独立、随机、相加。

3.3.2 真正搞懂泊松分布

1.泊松分布是什么

泊松分布的概率函数为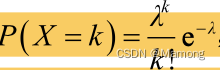 ，k=0，1，2，3...，其中，参数λ指单位时间(或单位面积)内事件发生的平均概率。泊松分布表达的含义是，单位时间里某事件发生了 λ 次， 那么事件发生 k 次的概率是多少。泊松分布适用的事件需要满足以下 3 个条件:第一，事件是小概率事件;第二，事 件之间相互独立;第三，事件的概率是稳定的。

2.泊松分布背后的原理是什么

泊松分布是二项分布的一种极 限形式，可以通过二项分布公式取极限推导出来。

泊松分布可作为二项分布的极限而得到。一般来说，若 ，其中 n 很 大、p 很小，则当 不太大时，X 的分布接近于泊松分布  。

3.4 理解朴素贝叶斯思想很重要

3.4.1 如何理解条件概率

已知事件 A 发生而求事件 B 发生的概率 P(B|A) 就是条件概率。

3.4.2 如何理解贝叶斯公式

3.4.3 贝叶斯公式的应用

3.4.4 最大似然估计

最大似然原理中的“最大似然”表示“最大概率看起来是这个样子”。

最大似然原理应该表述为，若一次试验有 n 个可能的结果， 分别为 A1,A2,...,An，现在做一次试验的结果为 Ai，那么我们可以认为本次试验的结果事件 Ai 在 这 n 个可能的结果中出现的概率最大。

最大似然估计实际上就是利用 最大似然原理完成一项任务:参数估计。

最大似然估计的目的是，利用已知样本结果，反推最有可能(最大概率)导致出现这样结 果的参数值是多少。最大似然估计是一种统计方法，属于统计学的范畴。最大似然原理是一种 基础原理，属于概率论的范畴。最大似然估计是建立在最大似然原理基础上的一种统计方法。 它通过现实中已经给定的观察数据来倒推和评估模型参数，例如经过若干次试验并观察结果， 构造试验结果概率的某个含参表达式，通过假定该概率值最大来求解参数值。