abstract

• 向量代数@向量基本概念和向量线性运算

向量的基本概念

• 平面向量和空间向量是类似的,这里主要以空间向量为主讨论

向量

• 既有大小(模)又有方向的量,称为向量(或矢量)
  • 印刷体常用黑体字母表示向量
  • 手写通常用头箭头表示向量
• 向量的大小也被称为模
• 只考虑方向和大小(而不考虑起点)的向量称为自由向量
• 这里的向量是抽象向量的一个简化版本$n$个数构成的数组,而在例如高等代数中讨论的,在线性空间中有含义更加广的向量以及更加深刻的性质研究

向量的坐标分解式和坐标👺

• 向量的坐标(表示):
  • 向量的终点在坐标轴上的投影坐标$a_x,a_y,a_z$叫做向量$\mathbf{a}$的坐标,记为$\mathbf{a}=(a_x,a_y,a_z)$
  • 向量的坐标分解式=$a_x\mathbf{i}+a_y\mathbf{j}+a_z\mathbf{k}$
• 更多详见向量坐标分解式相关章节

向量的模@向量的长度(大小)👺

• 向量的模:${\mathbf{a}}^T=(a_x,a_y,a_z)$,则$|\mathbf{a}|=\sqrt{a_x^2+a_y^2+a_z^2}$=$\sqrt{(a_x,a_y,z_y)\cdot (a_x,a_y,a_z)}$
  • 在空间直角坐标系中,该公式是根据勾股定理得到
  • $\mathbf{a}\cdot \mathbf{a}=a_x^2+a_y^2+a_z^2$,这里假设$\mathbf{a}$是列向量
  • 如果引入矩阵乘法(向量内积)的表示方法,还可以写作$|\mathbf{a}|=\sqrt{{\mathbf{a}}^T\mathbf{a}}$,其中${\mathbf{a}}^T,\mathbf{a}$分别是行向量以及其转置得到的列向量

零向量

• 零向量:模为0的向量称为零向量,其方向可以看作任意的,记为$0$或$\vec{0}$
• 由于零向量与另一个向量的夹角的取值在$[0,\pi ]$内任意取值,因此可以认为零向量和任意向量平行,也可以认为零向量和任意向量垂直

单位向量👺

• 单位向量:模为1的向量称为单位向量
  • 通常向量$\mathbf{a}$的同向单位向量记为${\mathbf{a}}^0$
  • 对于给定的一个方向$\mathbf{l}$,记该方向的单位向量为${\mathbf{e}}_{\mathbf{l}}$或${\mathbf{l}}_0$或${\mathbf{l}}^0$,或$\mathbf{u}$
• 每个方向都有单位向量,方向相同的向量的单位向量完全相同
• 不同方向的单位向量长度都为1,但是方向不同
• 向量的坐标和单位向量表示加法表示
  • 取$\mathbf{i}=(1,0,0)$,$\mathbf{j}=(0,1,0)$,$\mathbf{k}=(0,0,1)$,它们分别是$x,y,z$轴的方向单位向量
  • 则$\mathbf{a}=(a_x,a_y,a_z)=a_x\mathbf{i}+a_y\mathbf{j}+a_z\mathbf{k}$

方向向量

• 这个概念在讨论解析几何中的直线时,直线的点向式方程由直线的某个方向向量和直线上的一个点确定
• 方向向量不一定是单位向量
• 例如,直线$l$过$P_0(x_0,y_0)$,直线的某个方向向量为$(1,2)$,则方程可以表示为$\frac{x-x_0}{1}$=$\frac{y-y_0}{1}$

非零向量的单位向量@正规化

• 设非零向量$a=(a_x,a_y,a_z)$

  • $a^0=\frac{a}{|a|}$=$\frac{1}{|a|}(a_x,a_y,a_z)$

• 使用范数表示

  • $||a||$表示向量$a$的$L^2$范数

  • $\beta =\frac{1}{||\alpha ||}\alpha$的长度一定是1

  • $||\beta ||$=$\left|\left|\frac{1}{||\alpha ||}\alpha \right|\right|$=$\frac{1}{||\alpha ||}||\alpha ||=1$

向量夹角👺

• 向量夹角
  • 设向量$a=\overrightarrow{OA},b=\overrightarrow{OB}$,则他们的夹角记为$\theta =\angle AOB=<a,b>,且\theta \in [0,\pi ]$
    • 若$\theta =0$,则$a,b$同向
    • 若$\theta =\pi$,则$a,b$反向
    • 两者统称为$a,b$平行,记为$a\parallel b$
    • 若$a=\lambda b$,则$a,b$平行
      • 若$\lambda >0$,$a,b$同向
      • 若$\lambda <0$,$a,b$反向
  • 若$\theta =\frac{\pi }{2}$,则$a\perp b$

向量方向角和向量间夹角@投影

• 另见向量的方向角和方向余弦@向量间夹角余弦@投影和向量分量

几何描述向量的线性运算

• 平面二维向量和空间三维向量的运算类似

向量的加减运算

• 借助平行四边形或三角形法则,从几何的角度描述向量的加法和减法

• 并且减法可以转换为加法$\mathbf{a}-\mathbf{b}=\mathbf{a}+(-\mathbf{b})$

• 向量加减运算的代数(坐标)运算比较简单,只需要将向量对应分量相加减:$\mathbf{a}\pm \mathbf{b}$=$(a_x\pm b_x,a_y\pm b_y,a_z\pm b_z)$

• 向量加法满足交换律和结合律

• 

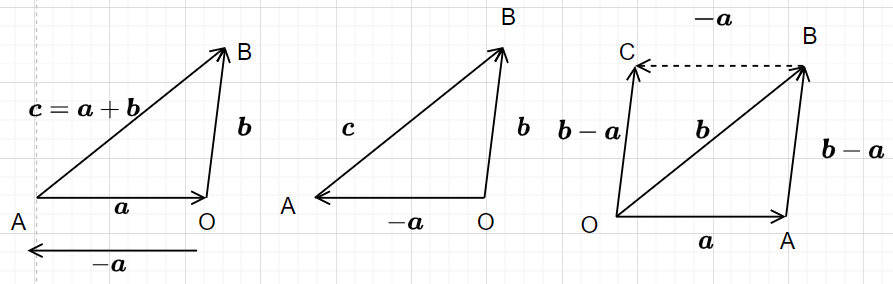
  • $\mathbf{c}=\overrightarrow{AB}$=$\overrightarrow{AO}+\overrightarrow{OB}
    $=$\overrightarrow{OB}-\overrightarrow{OA}$
  • 并且$|\mathbf{a}-\mathbf{b}|=|\mathbf{b}-\mathbf{a}|$

向量的三角形三边不等式

• 由三角形两边之和大于第三边,对应向量三角形法则下的向量加法和向量减法满足不等式:

  • $|\mathbf{a}+\mathbf{b}|⩽|\mathbf{a}|+|\mathbf{b}|$

  • $|\mathbf{a}-\mathbf{b}|$=$|\mathbf{b}-\mathbf{a}|⩽|\mathbf{a}|+|\mathbf{b}|$

• 等号在$\mathbf{a},\mathbf{b}$同向或反向时成立

数乘

• 设$\lambda$是一个数,$\lambda \mathbf{\alpha }$是一个向量,$|\lambda \mathbf{\alpha }|=|\lambda ||\mathbf{\alpha }|$

  • 当$\lambda >0$,$\lambda \mathbf{\alpha }$与$\mathbf{\alpha }$同向
  • 当$\lambda =0$,$\lambda \mathbf{\alpha }=0$
  • 当$\lambda <0$,$\lambda \mathbf{\alpha }$和$\mathbf{\alpha }$反向

• 代数表示:设$\mathbf{\alpha }=(a_x,a_y,a_z)$,则$\lambda \mathbf{\alpha }=(\lambda a_x,\lambda a_y,\lambda a_z)$

• $|\lambda \mathbf{\alpha }|$=$\sqrt{(\lambda a_x{)}^2+(\lambda a_y{)}^2+(\lambda a_z{)}^2}$=$\sqrt{{\lambda }^2(a_x^2+a_y^2+a_z^2)}$=$|\lambda ||\mathbf{\alpha }|$

• 向量的数乘满足结合律和分配律

方程的思想求解向量相关问题

• 例如求空间中满足某个特征的点的坐标

• 使用建立方程并解方程的方法可以简化思维过程

• 

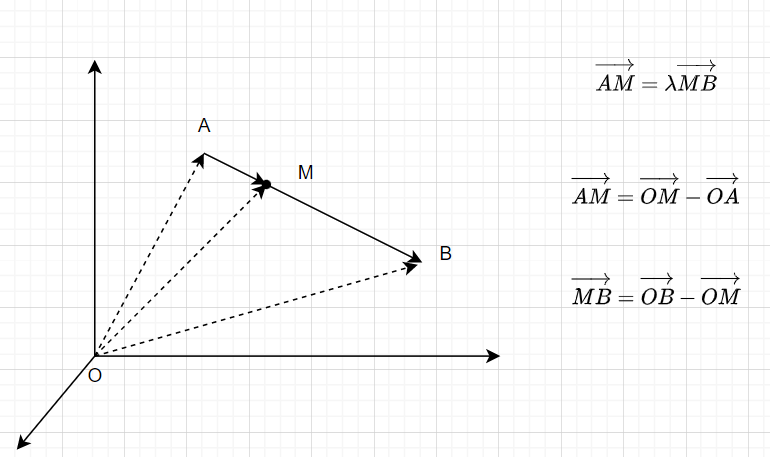
• 设$\overrightarrow{AM}=\lambda \overrightarrow{MB}$,$A=(x_1,y_1,z_1),B=(x_2,y_2,z_2)$

• 其中:

  • $\overrightarrow{AM}$=$\overrightarrow{OM}-\overrightarrow{OA}$
  • $\overrightarrow{MB}$=$\overrightarrow{OB}-\overrightarrow{OM}$

• 所以$\overrightarrow{OM}-\overrightarrow{OA}=\lambda (\overrightarrow{OB}-\overrightarrow{OM})$

  • $(1+\lambda )\overrightarrow{OM}$=$\lambda \overrightarrow{OB}+\overrightarrow{OA}$
  • $\overrightarrow{OM}$=$\frac{1}{1+\lambda }(\overrightarrow{OA}+\lambda \overrightarrow{OB})$=$\frac{1}{1+\lambda }(x_1+\lambda x_2,y_2+\lambda y_2,z_1+\lambda z_2)$

向量的线性运算的坐标表示公式

• 利用坐标作向量的线性运算(加法,减法,数乘)是方便的

• 向量的坐标分解式对应了坐标在各个轴上的分量

• 利用相关交换律和结合律,可得

  • $\mathbf{a}+\mathbf{b}$=$(a_x+b_x)\mathbf{i}+(a_y+b_y)\mathbf{j}+(a_z+b_z)\mathbf{k}=(a_x+b_x,a_y+b_y,a_z+b_z)$
  • $\mathbf{a}-\mathbf{b}$=$(a_x-b_x)\mathbf{i}+(a_y-b_y)\mathbf{j}+(a_z-b_z)\mathbf{k}=(a_x-b_x,a_y-b_y,a_z-b_z)$
  • $\lambda \mathbf{a}$=$\lambda (a_x,a_y,a_z)$