---

洛谷里面8页题解千篇一律，就没有用线段树求解的，这下不得不由本蒟蒻来生啃又臭又硬，代码又多的线段树了。

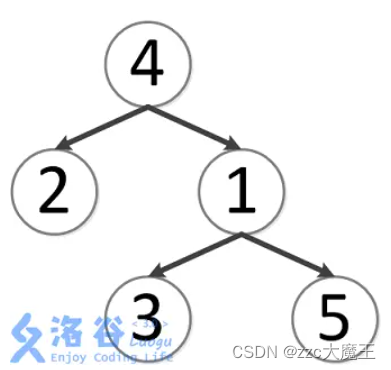
样例的欧拉序列：4 2 4 1 3 1 5 1 4

记录每个节点最早在欧拉序列中的时间，任意两个节点的LCA就是他们两个节点在欧拉序列之间，深度最小的那一个。（证明看洛谷题解）

比如2和5的LCA：4 2 4 1 3 1 5 1 4，4是深度最小的。

很显然这是RMQ问题，可以用ST表求解，但我偏不，多次询问区间求极值可以用线段树来维护。

此处维护的就是

注意建树内存大小是维护欧拉序列的大小，而不是原序列，欧拉序列是原序列的2倍大小，所以线段数要开8倍的内存。

AC代码

#include <bits/stdc++.h>
using namespace std;
const int N=5e5+1;

int n,m,s,oula[N<<1],d[N],ti[N],t[N<<3];//注意是8倍大小
vector<int>e[N];
bitset<N>vis;

inline int read(){
    int x=0;char c=getchar();
    while(c<48 or c>57)c=getchar();
    while(c>=48 and c<=57)x=(x<<3)+(x<<1)+(c xor 48),c=getchar();
    return x;
}

int main(){
    n=read(),m=read(),s=read();
    for(int i=1,x,y;i<=n-1;++i){
        x=read(),y=read();
        e[x].push_back(y);
        e[y].push_back(x);
    }
    
    d[s]=1,n=0;
    auto dfs=[](int x,auto dfs){
        if(vis[x])return;
        vis[x]=true;
        oula[++n]=x;//欧拉序列
        for(auto i:e[x]){
            if(!vis[i]){
                d[i]=d[x]+1;//深度
                dfs(i,dfs);
                oula[++n]=x;//欧拉序列
            }
        }
    };dfs(s,dfs);
    for(int i=1;i<=n;++i)if(!ti[oula[i]])ti[oula[i]]=i;//欧拉时间戳

    auto build=[](int l,int r,int i,auto build){
        if(l==r){
            t[i]=l;//叶子节点,欧拉时间戳
            return;
        }
        int mid=l+r>>1;
        build(l,mid,i<<1,build);
        build(mid+1,r,i<<1|1,build);
        t[i]=d[oula[t[i<<1]]]<d[oula[t[i<<1|1]]]?t[i<<1]:t[i<<1|1];
    };build(1,n,1,build);
    
    d[0]=INT_MAX;
    for(int i=1,a,b;i<=m;++i){//线段树维护欧拉时间戳
        a=read(),b=read();
        if(ti[a]>ti[b])swap(a,b);
        auto query=[](int l,int r,int i,int x,int y,auto query){
            int ans=0;
            if(l>=x and r<=y)return t[i];//返回欧拉时间戳
            int mid=l+r>>1;
            if(x<=mid){
                int idx=query(l,mid,i<<1,x,y,query);
                ans=d[oula[idx]]<d[oula[ans]]?idx:ans;
            }
            if(y>mid){
                int idx=query(mid+1,r,i<<1|1,x,y,query);
                ans=d[oula[idx]]<d[oula[ans]]?idx:ans;
            }
            return ans;
        };printf("%d\n",oula[query(1,n,1,ti[a],ti[b],query)]);
    }
    return 0;
}

需要注意的是，开O2并不会带来任何优化，本蒟蒻代码是厌氧代码。