这里先回顾一下预积分是怎么来的
VINS-Mono-IMU预积分 （三：为什么要预积分+预积分推导）
这里贴出预积分的公式

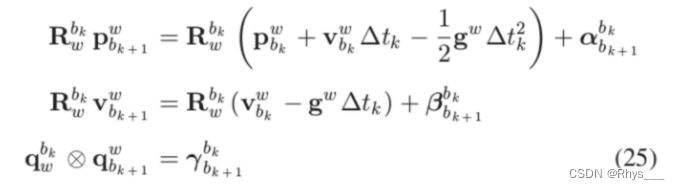
具体含义解释看对对应的文章
整个误差函数如下

预积分 $\alpha$ $\beta$ $\gamma$ 是用 IMU 预积分获得的增量（前面用了大篇幅去推导，可以看之前的文章），左边是优化获得的增量，整体就是优化后的值不能离预积分的增量太远，太远的话误差值就会变大
对于四元数就是旋转后的相乘结果尽可能为 0 ，$\theta \to 0,q=[1,\frac{\vec{n}\theta }{2}]$，这里有个 $\frac{1}{2}$ ，所以要乘个2
代码中实际的写法是 $({\gamma }_{b_{k+1}}^{b_k}{)}^{-1}\otimes (q_{b_k}^w{)}^{-1}\otimes q_{b_{k+1}}^w$ ，含义是一样的

注意：
这个残差计算是每次优化后都会进来计算的，$k+1$ 时刻（代码中的 $j$）的值就是待优化的值，每次进入函数计算都会被改变，具体计算方法和上面的公式一样，疑问：感觉好像是 $i$ 和 $j$ 的值同时优化的，后面具体看看代码优化量是哪个？
由于零偏 $Ba$ 也是优化变量，而预积分又与零偏有关系，零偏改变了理论上是要重新积分的，但是由于这个零偏量变化很小，所以这里采用一阶近似的方式来更新预积分，更新的预积分继续作为这个约束，零偏更新建模看这篇文章VINS-Mono-IMU预积分 （七：预积分零偏建模方式）
这就是所谓的紧耦合，就是又作为约束又同时优化自身变量

预积分协方差矩阵的使用
前面算出残差 $e$ 后，还需要成上信息矩阵（协方差）才行，因为虽然预积分作为约束，但是不是说这个约束是绝对准确的，它是有一个置信度的，前面通过ESKF就是为了计算预积分的置信度

由于现在设置的预积分约束因子，所以前面计算的预积分置信度就是用在这里计算的残差上面，公式为 $e^{T}Pe$，对置信度 $P$ 进行 $L{L}^T$ 分解，这个分解相当于是对 $P$ 开根号，那么新的残差用 $L^{T}e$ 来当作新的残差。
代码中对置信度取逆是因为，协方差越大代表不确定性越高，则权重应该越小，所以要取逆