一、中国剩余定理

1、作用：

我们上一章节中，详细地讲解了如何利用扩展欧几里德算法解一个线性同余方程，但是如果我们遇到了线性同余方程组的话，我们就需要用到今天所讲解的中国剩余定理。

但是中国剩余定理的成立前提是，方程组中的模数两两互质。

2、内容：

对于方程组：

$$\{\begin{array}{l}x\equiv a_1(mod{m}_1)\\ x\equiv a_2(mod{m}_2)\\ x\equiv a_3(mod{m}_3)\\ ...\\ x\equiv a_n(mod{m}_n)\end{array}$$
最终的结果

$$x=\sum _{k=1}^n{a}_k{c}_k{c}_k^{-1}$$

其中：

$$M=\prod _{k=1}^n{m}_k$$
$$c_k=\frac{M}{m_k}$$
$c_k^{-1}$是模数为$m_k$的时候，$c_k$的逆元。

3、证明：

（1）逆元的存在性

我们先证明一下，逆元$c_k^{-1}$是存在的。

因为$m$之间是互质的，而$c_k$中不含有$m_k$。因此，$gcd(c_k,m_k)=1$

由裴蜀定理可知：

存在 $x{c}_k+y{m}_k=1$

即：$x{c}_k=-y{m}_k+1$

即：$x{c}_k\equiv 1(mod{m}_k)$

此时的$x$就是逆元$c_k^{-1}$，所以逆元必定是存在的。

（2）验证定理的正确性

假设一个$c_i$

当$i==k$的时候，

$c_i\ast c_i^{-1}\equiv 1mod(m_k)$

两侧同时乘$a_i$

$a_i{c}_i\ast c_i^{-1}\equiv a_{i}mod(m_k)$

当$i!=k$的时候，

此时的$c_i$当中是存在$m_k$的，不存在的是$m_i$

由于$c_i$包含了$m_k$，所以此时$c_i|m_k$

即$c_i\%m_k=0$

两边同时乘以$a_i{c}_i^{-1}$还是$0$

因此，综合上述两种情况：
我们的$x\%m_k=0+0+...+a_k{c}_k{c}_k^{-1}+0$

即：

$x\equiv a_k{c}_k{c}_k^{-1}mod(m_k)$

因为在第一种情况下，我们得到了：

$a_k{c}_k\ast c_k^{-1}\equiv a_{k}mod(m_k)$

所以：

$x\equiv a_{k}mod(m_k)$

符合我们的方程组。因此这个结论是正确的。

4、代码实现：

（1）步骤：

第一步：计算$M$

第二步：计算$c_i$

第三步：计算$c_i^{-1}$（利用扩展欧几里德算法）

这里讲解一下如何计算逆元$c_i^{-1}$

$c_i\ast c_i^{-1}\equiv 1(mod{m}_i)$

即：

$c_i{c}_i^{-1}+y{m}_i=1$

这个式子中，我们不知道的未知数有两个，一个是$c_i^{-1}$，另一个是$y$。

但我们知道的是：$c_i,m_i$

所以我们可以用扩展欧几里德算法+裴蜀定理

计算出$x\ast c_i+y\ast m_i=gcd(c_i,m_i)$

而$gcd(c_i,m_i)=1$

所以，我们用这两个式子求的就是，我们的目标变量
$c_i^{-1}$和$y$

也就是说，我们的$x=c_i^{-1}$

第四步：套用中国剩余定理

（2）问题：

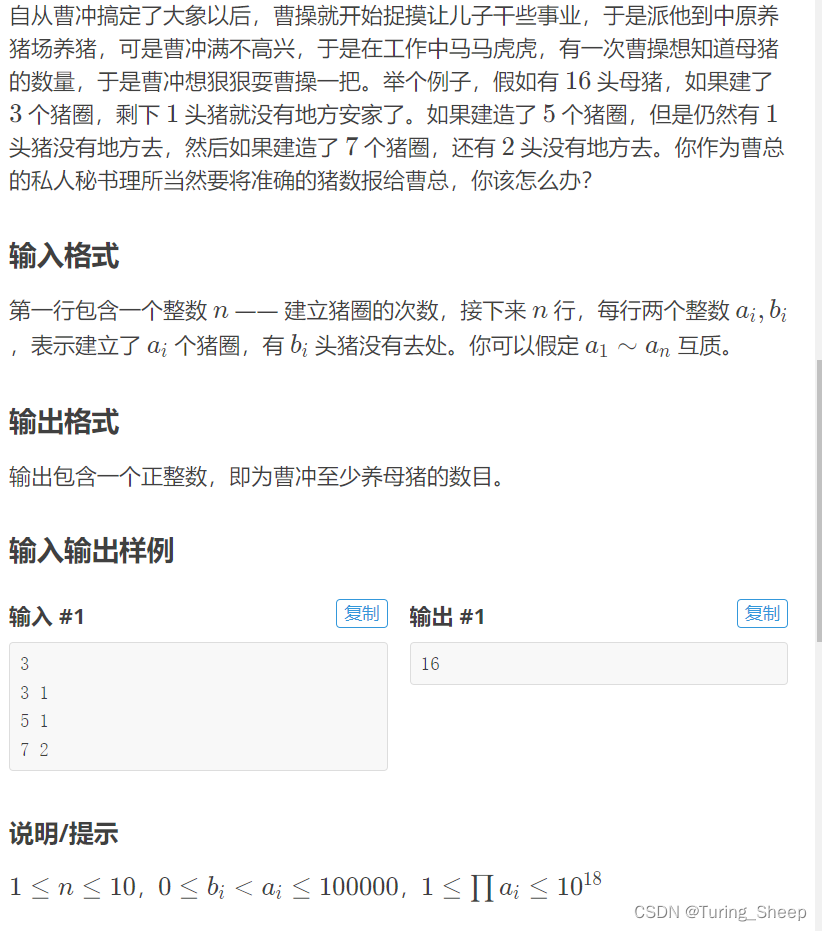
洛谷：中国剩余定理模板题

（3）代码：

#include<iostream>
using namespace std;
typedef long long LL;
const int N=1e5+10;
int n;
LL m[N],a[N];
//扩展欧几里德算法
LL exgcd(LL a,LL b,LL&x,LL&y)
{
    if(b==0)
    {
        x=1,y=0;
        return a;
    }
    else
    {
        LL res=exgcd(b,a%b,x,y);
        LL tmp=y;
        y=x-a/b*y;
        x=tmp;
        return res;
    }
}
//中国剩余定理
LL CRT(LL m[],LL a[])
{
    LL M=1,ans=0;
    //计算M
    for(int i=1;i<=n;i++)M*=m[i];
    for(int i=1;i<=n;i++)
    {
    	//得到ci
        LL c=M/m[i],x,y;
        //计算逆元
        exgcd(c,m[i],x,y);
        //利用中国剩余定理公式
        ans=(ans%M+a[i]*c*x%M)%M;
    }
    //返回答案
    return (ans%M+M)%M;
}

int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d",&m[i],&a[i]);
    }
    cout<<CRT(m,a)<<endl;
    return 0;
}