作者：学Java的冬瓜
博客主页：☀冬瓜的主页🌙
专栏：【Java 数据结构】
分享：美妙人生的关键在于你能迷上什么东西。——《球状闪电》
主要内容：优先级队列底层的堆，大堆的创建，插入，删除。堆的算法的时间复杂度。Java中的对象的比较。

一、模拟实现优先级队列

JDK1.8中，PriorityQueue(优先级队列)底层使用了堆的数据结构。

1、什么是堆？

1> 堆是在完全二叉树的基础上变化得到的(取决于它的存储使用数组，如果是非完全二叉树，则浪费空间)。
2> 堆的特点：在每棵树(子树)中，都是根节点最大（大堆）或者根节点最小（小堆）。

2、代码

2.1、建堆(大堆示例)

建堆有两种方式：
第一种是从无到有(相当于第二种的插入元素，每次插入都调整为堆)
第二种是给一个数组，直接把它调整为堆。以下方法就是第二种。

public class MyHeap {
	// 1、堆的基本框架
    private int elem[];
    private int usedSize;
    private static final int DEFAULT_SIZE=11; // 注意：PriorityQueue源码中就是默认先开11个空间
    // 利用构造方法初始化
    public MyHeap() {
        elem = new int[DEFAULT_SIZE];
    }
    // 2、把数组放进堆数组
    public void initMyHeap(int[] arr){
        for(int i = 0; i < arr.length; i++){
            elem[i] = arr[i];
            usedSize++;
        }
    }
	// 3、建堆，以parent为根节点的树依次调整为大堆
    public void createHeap(){
        for (int parent = (usedSize-1-1)/2; parent >= 0; parent--) {  // 注意：数组下标到0
            shiftDown(parent, usedSize);
        }
    }

    // 向下调整算法
    private void shiftDown(int parent, int len){
        int child = parent*2+1;
        while(child < len){  // 注意：len-1为堆数组中最后一个元素的下标
            if(child+1 < len && elem[child] < elem[child+1]){// 左右孩子都满足下标在范围内。
                child++;// 找到以parent为根节点的左右孩子中大的
            }
			
            if(elem[child] > elem[parent]){
                int tmp = elem[child];
                elem[child] = elem[parent];
                elem[parent] = tmp;
				
				// 满足交换条件，就交换，然后继续往下判断，是否符合条件
                parent = child;
                child = parent*2+1;
            }else{
            	// 不满足交换条件，就说明已经满足大堆的要求，直接break
                break;
            }
        }
    }

2.2、堆的插入

    public int offer(int data){
    	// 1、插入元素到堆中
        if(heapIsFull()){
            grow();
        }
        elem[usedSize] = data;
        usedSize++;
		
		// 2、把最后一个元素通过向上调整放在对应位置
        shiftUp(usedSize-1); // 注意：usedSize-1才是data元素的下标

        return data;
    }
    // 向上调整算法
    private void shiftUp(int child){
        int parent = (child-1)/2;
        while(parent >= 0){
        	// 把孩子节点和父亲节点比较，孩子大就交换
            if(elem[child] > elem[parent]){
                int tmp = elem[child];
                elem[child] = elem[parent];
                elem[parent] = tmp;

                child = parent;
                parent = (child-1)/2;
            }else {
                break;
            }
        }
    }
    // 判断堆满
    private boolean heapIsFull(){
        return this.usedSize == this.elem.length;
    }
    // 扩容
    private void grow(){
        elem = Arrays.copyOf(this.elem, this.usedSize*2);
    }

2.3、堆的删除

	// 删除队头元素
    public int poll(){
        if(heapIsEmpty()){
            return -1;
        }
		// 把堆顶和
        int tmp = elem[0];
        elem[0] = elem[usedSize-1];
        elem[usedSize-1] = tmp;
        usedSize--;

        shiftDown(0,usedSize);

        return elem[usedSize];
    }
    // 堆空
    private boolean heapIsEmpty(){
        return this.usedSize == 0;
    }

2.4、获取堆顶元素

// 获取队头(堆顶)元素
    public int peek(){
        return elem[0];
    }
}

3、小练习

4、堆的总结

• 建堆，有两种方法：法一是不断插入数据，不断调整为堆，法二是根据一个数组，直接调整为堆。下面都为法二的总结。
• 建大堆：因为要求每棵子树都为大堆，1> 所以可以从调整最后一个节点的父节点为根节点的树，开始往上调整其它树。2> 每棵子树的调整都用向下调整算法：即左右孩子中大的节点比根节点还大，就把两者交换。
• 堆的插入：1> 把新增元素先放在堆的完全二叉树的最后。 2> 使用向上调整算法，把堆里最后一个元素调整到正确的位置。
• 堆的删除：1> 把堆顶元素和最后一个元素交换，然后堆的有效元素个数-1，2> 把堆顶元素使用向下调整算法放到正确位置。
• 向下调整算法：建堆、删除堆顶元素都需要用到。要判断左右孩子谁大，大的再和父亲节点交换。然后再parent = child，child = parent*2+1继续往子树判断是否满足大堆，不满足则一直交换，直到child=有效元素个数(越界)。
• 向上调整算法：插入元素用到向上调整算法，只是插入的这个child和它的parent比较，不满足大堆交换，直到child>0结束(或者parent>=0结束)，不需要左右孩子比较。

二、算法的复杂度分析

1、调整算法复杂度

log(n)
1> 从代码上来看，向上调整算法和向下调整算法，都是孩子节点和父亲节点之间的交换，所以复杂度应该是树的高度
2> 又因为堆是完全二叉树，所以调整算法的复杂度(最坏)为log(n)

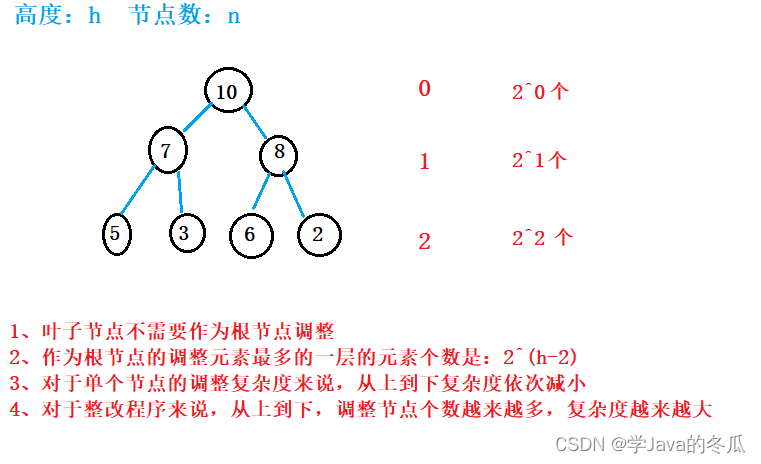
2、建堆的时间复杂度（重点）

三、PriorityQueue关于比较的分析

1、关于PriorityQueue的分析

• 当没有传入数组容量的时候，默认数组大小是11.
• 扩容时，当oldCapacity<64，就约为2倍扩容，当oldCapacity>=64，就为1.5倍扩容。
• 当没有传入比较器的时候，你放进PriorityQueue里面的必须是可比较的（比如整形，或者比如Student类实现Compareable接口，重写compareTo方法）
• 在PriorityQueue中整形数默认是小堆排序，如果想要实现大堆，可以使用比较器。不能实现Compareable重写compareTo方法，因为我不能改变Integer类的源码。

2、关于比较的分析

法一：用equals方法

equals方法只能判断两个元素是否相等，或者地址是否相等

法二：实现Compareable接口

让类实现Compareable接口，然后重写compareTo方法，在比较时，程序自动调用compareTo方法

public class Student implements Comparable<Student>{
    private String name;
    private int age;
    public Student(){
        
    }

    @Override
    public int compareTo(Student o) {
        return this.age - o.age;
    }
}

法三：比较器

<1> 制造比较器类

//构造：让构造器类实现Comparator接口，重写compare方法
class AgeCmp implements Comparator<Student>{
    @Override
    public int compare(Student o1, Student o2) {
        return o1.age - o2.age; // 为了方便，这里的Student类的age字段，我没有封装
    }
}

//使用(main中)：
PriorityQueue<Student> priorityQueue = new PriorityQueue<>(new AgeCmp());

<2> 利用内部类完成比较器

		//在main中
		// 利用内部类给构造器进行构造
		PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o2 - o1;
            }
        });

法四：lambda表达式（JDK1.8开始出现）

PriorityQueue<Integer> priorityQueue = new PriorityQueue<>((x,y)->{return x-y;});
//或者
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>((x,y)->x.compareTo(y));
// 或者
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(Integer::compareTo);