GNN基础知识

news2025/4/8 13:11:29

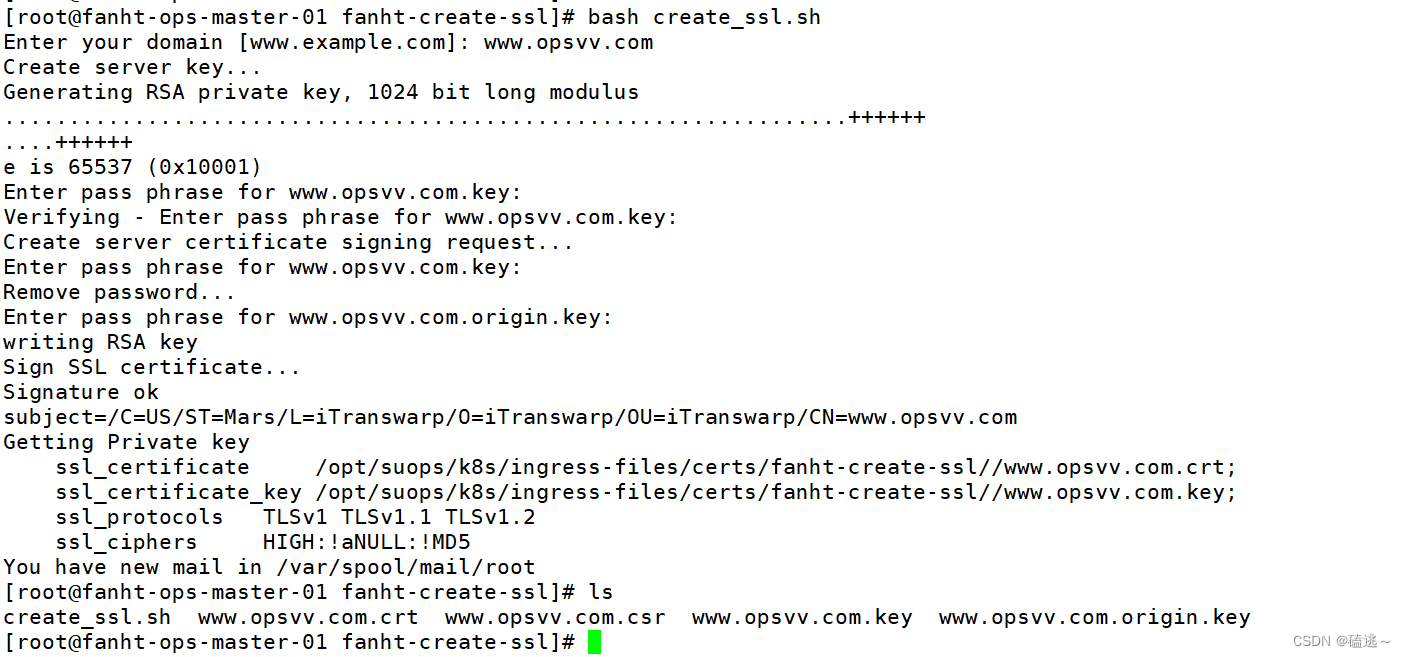
1. 泰勒公式

背景background

有一个很复杂的方程，我们直接计算方程本身的值可能非常麻烦。

所以我们希望能够找到一个近似的方法来获得一个足够近似的值

本质：

近似，求一个函数的近似值

one point is 近似的方法
another point is 近似的精度

泰勒公式原理

通过斜率逼近

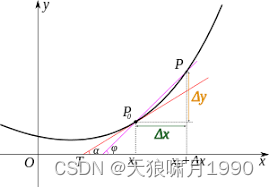
原理：经典的导数图，从上图可以看到，随着△x减小，间p0和点p也会越来越接近，这就带来了△y越来越接近△x·f'(x0)。

当然，当△x比较大时误差就会比较大，为了缩小误差，我们可以引入二阶导数、三阶导数以及高阶导数。由于最终不知道究竟要有多少阶导数，不妨假设f(x)在区间内一直有n+1阶导数。

To 与原值误差越来越小

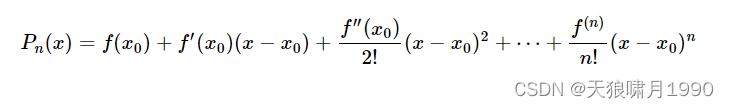
$p_{n}(x_{0}) \approx f(x_{0}) \\ p_{n}(x_{0}) \approx f(x_{0}) + f'(x_{0})(x-x_{0}) \\ p_{n}(x_{0}) \approx f(x_{0}) + f'(x_{0})(x-x_{0}) + f''(x_{0})\frac{(x-x_{0})^{2}}{2!}\\ .....$

分析

以导函数图为例，用f(x0)去近似f(x)，f(x0)加上f'(x0)(x-x0)，仍然与真实值差着一小块误差e2: f(x)-△y，对于e2，继续用二阶导f''(x0)去加，去缩小f(x)-△y之间的误差。

2. Jacobian Matrix雅克比矩阵

假设F：Rn -> Rm是一个从n维欧式空间映射到m维欧式空间的函数，这个函数由m个实函数组成y1(x1,x2,...,xn),....,ym(x1,x2,...,xn)。这些函数的偏导数(如果存在)可组成一个m行n列的矩阵，即Jacobian matrix。

Meaning： $J_{F}(p)$ 这个线性映射即F在点p附近的最佳线性逼近。当x足够靠近p时，

$F(x) \approx F(p) + J_{F}(x-p)$

区别：

Jacobian matrix: 两个不同空间，点p逼近x
Taylor series approximation：同一空间中，点p逼近点x

3. Laplacian matrix拉普拉斯矩阵

梯度gradient，矢量：该点处的导数沿该方向去的最大值，即变化率最大，可以简单理解为导数。

散度divergence，标量：表示空间中各点矢量场发散的强弱程度。

拉普拉斯算子：n维欧式空间中的一个二阶微分算子，定义为梯度的散度。

$\Delta f = \sum_{i} \frac{\ni ^{2}f}{\ni^{2}xi}$

Meaning: 拉普拉斯算子计算了周围点与中心点的梯度差。

拉普拉斯矩阵：加权度矩阵 - 邻接矩阵，对称矩阵

$L = \sum_{i\in Ni} \sum_{j\in Nj} W_{ij}f_{i} - \sum_{j\in Nj}W_{ij}f_{j}=D -A$

证明：用简单的一阶向量模拟矩阵去证明，不然展开计算太麻烦！

4. 图傅里叶变换Graph Fourier Transformation

傅里叶变换：

$F(w) = \frac{1}{2\pi } \int_{-\infty }^{\infty}f(t)e^{-iwt}dt$

傅里叶变换是将函数f(t)拆解成无数个不同频率正弦波之和的过程，F(w)表示角频率为w的波的系数。
函数f(t)为基函数 $e^{-iwt}$ 投影，F(w)就表示w对应基上的坐标。

Meaning：函数f(t)可以想象成一个长度为无穷的向量，函数空间中的内积定义为积分，上面的傅里叶变换公式，将 $e^{-iwt}$ 看作基，则整个式子就是在算f(t)在 $e^{-iwt}$ 这个基上的坐标，所有的w都要算一次，就可以得到f(t)在 $e^{-iwt}$ 这组基上的完整坐标，即F(w)。