前言

  支持向量机$(Support$ $Vector$ $Machine,SVM)$源于统计学习理论，是一种二分类模型，是机器学习中获得关注最多的算法，没错，是“最”，没有之一。

1. 间隔与支持向量

  支持向量机分类方法的核心思想就是在特征空间中找出一个超平面作为决策边界，来将样本划分为正类和负类，并使模型在未知数据集上的泛化误差尽可能的小。

  超平面：在几何中，超平面是一个空间的子空间，它是维度比所在空间小一维的空间。 如果数据空间本身是三维的，则其超平面是二维平面，而如果数据空间本身是二维的，则其超平面是一维的直线。

  比如上面这组数据，我们很容易就可以画出一条线将上面的数据划分为两个类别，而且其误差为零。对于一个数据集来说，这样误差为0的超平面可能有很多个，比如下面这样：

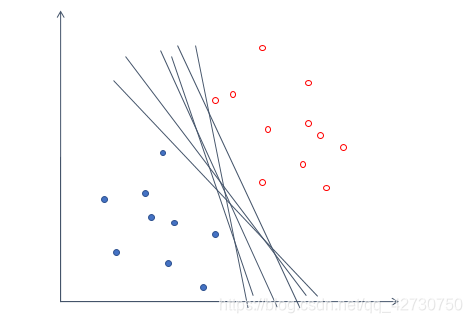
  但这样的模型不能保证泛化性能很好，即无法保证这个超平面在未知数据集上也表现很优秀。因此我们引入了一个名词------间隔$(margin)$，就是将我们找到的超平面向两边进行平移，直到碰到离这个超平面最近的样本点后停下，形成两个新的超平面，这两个超平面的距离就叫“间隔”，超平面处于这个“间隔”的中间位置，即我们选择的超平面到平移后的两个新的超平面之间的距离相等。而距离超平面最近的几个样本点称为支持向量$(support$ $vector)$。

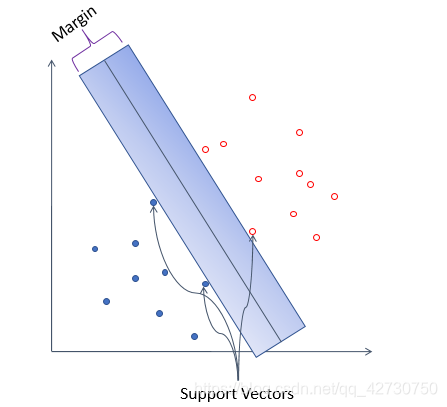
  比较一下上面两个图，直观上来看，都能够将样本换分为了两类，但如果再往里面加入一些噪声呢，很明显，蓝色的那个超平面对局部扰动的容忍性最好，因为它“够宽”，如果想象不出来，看下面这个例子：

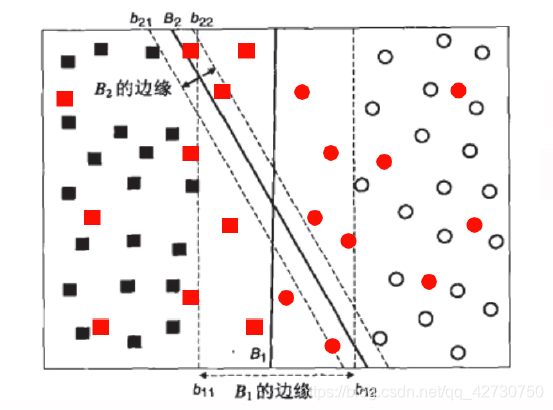
  很明显，引入了一些新的数据样本后，$B_1$这个超平面误差依旧为0，分类结果是最鲁棒的，$B_2$这个超平面因为间隔较小，所以出现了分类误差。因此我们在寻找超平面时，希望间隔越大越好。
  以上就是支持向量机，即通过找出间隔最大的超平面，来对数据进行分类的分类器。
  支持向量机的模型由简至繁可以分为下面三种：
  $\bullet$ 线性可分支持向量机
  $\bullet$ 线性支持向量机
  $\bullet$ 非线性支持向量机
  当训练数据线性可分时，通过硬间隔最大化$(hard$ $margin$ $maximization)$，学习一个线性的分类器，即线性可分支持向量机，又称为硬间隔支持向量机；当训练数据集近似线性可分时，通过软间隔最大化$(soft$ $margin$ $maximization)$，也学习一个线性的分类器，即线性支持向量机，又称为软间隔支持向量机；当训练数据集线性不可分时，通过使用核技巧$(kernel$ $trick)$及软间隔最大化，学习非线性支持向量机。

  简单是复杂的基础，也是复杂的特殊情况嘛

2. 函数方程描述

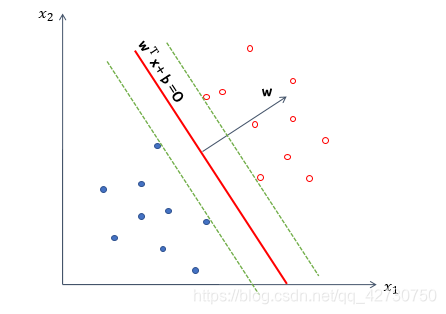
  假设给定数据集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x n , y n ) } , y i ∈ { − 1 , + 1 } D=\{(x_1,y_1),(x_2,y_2),\dots,(x_n,y_n)\},y_i \in \{-1,+1\} D={(x1​,y1​),(x2​,y2​),…,(xn​,yn​)},yi​∈{−1,+1}，在上述在样本空间中，任意一条线都可以表示为：$${\mathbf{w}}^T\mathbf{x}+b=0$$  其中$\mathbf{w}=(w_1,w_2,\dots ,w_d{)}^T$为法向量，决定了超平面的方向；$b$为位移项，决定了超平面与原点之间的距离。很显然，超平面也可以被法向量$\mathbf{w}$和位移$b$确定。
  为了推导和计算简便，我们做出以下规定：
  在超平面以上的点都标记为正，超平面以下的点都标记为负，即对于$(x_i,y_i)\in D$，若$y_i=+1$，则有${\mathbf{w}}^T{\mathbf{x}}_i+b>0$；若$y_i=-1$，则有${\mathbf{w}}^T{\mathbf{x}}_i+b<0$，表达式如下：$$\{\begin{array}{ll}{\mathbf{w}}^T{\mathbf{x}}_i+b\ge +1,& y_i=+1\\ & \\ {\mathbf{w}}^T{\mathbf{x}}_i+b\le -1,& y_i=-1\end{array}$$  其中，+1和-1表示两条平行于超平面的虚线到超平面的相对距离。
  那么，样本空间中任意点$\mathbf{x}$到超平面的距离可以写为：$$r=\frac{|{\mathbf{w}}^T+b|}{||\mathbf{w}||}$$  由此也可以求得两个不同标签的支持向量到超平面的距离之和，也就是间隔，可以表示为：$$\gamma =\frac{2}{||\mathbf{w}||}$$  我们的目标就是找到最大间隔的超平面，也就是要满足如下约束的参数$\mathbf{w}$和$b$，使得$\gamma$最大，即$$\begin{gathered} \underset{\mathbf{w},b}{\max }\frac{2}{||\mathbf{w}||} \\ subjectto{y}_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1,i=1,2,\dots ,n \end{gathered}$$  很显然，最大化间隔$\gamma$只需要最小化$||\mathbf{w}||$即可，所以约束变成如下：$$\begin{gathered} \underset{\mathbf{w},b}{\min }\frac{1}{2}||\mathbf{w}|{|}^2 \\ subjectto{y}_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1,i=1,2,\dots ,n \end{gathered}$$

  实际上就是取一下倒数，那为啥又加上平方了呢，前面其实说过了，$L_2$范式嘛，加个平方是为了消除开平方的操作，简化计算过程。

3. 参数求解

  求解带有约束的最优化问题，一般常用的就是引入拉格朗日乘子$\lambda$构造拉格朗日函数。其实这属于多元函数的条件极值问题，可参考高数下册书中多元函数的条件极值与拉格朗日乘数法$(standardLagrangemultipliermethod)$，下面简单回顾一下。

3.1 拉格朗日乘数

  要找函数$z=f(x,y)$在附加条件$\phi (x,y)=0$下的可能极值点，可以先作拉格朗日函数$$L(x,y)=f(x,y)+\lambda \phi (x,y)$$  其中，$\lambda$为参数，求其对$x$、$y$和$\lambda$的一阶偏导数，并使之为零，然后联立方程：$$\{\begin{array}{l}{f}_x(x,y)+\lambda {\phi }_x(x,y)=0\\ \\ f_y(x,y)+\lambda {\phi }_y(x,y)=0\\ \\ \phi (x,y)=0\end{array}$$  有这个方程组解出$x$、$y$和$\lambda$，这样求得的$(x,y)$就是函数$f(x,y)$在附加条件$\phi (x,y)=0$下的可能极值点。
  如果函数的自变量多于两个，且附加条件多于一个，比如，要求函数$$u=f(x,y,z,t)$$在附加条件$$\begin{gathered} \phi (x,y,z,t)=0 \\ \psi (x,y,z,t)=0 \end{gathered}$$下的极值，可以先作拉格朗日函数$$L(x,y,z,t)=f(x,y,z,t)+\lambda f(x,y,z,t)+\mu f(x,y,z,t)$$  其中，$\lambda ,\mu$为参数，求其对$x$、$y$、$z$、$t$、$\lambda$和$\mu$的一阶偏导数，并使之为零，然后联立方程求解出$(x,y,z,t)$。

  来，看一个小题：
  求函数$u=x^2+y^2+z^2$在约束条件$z=x^2+y^2$和$x+y+z=4$下的最大值与最小值。

3.2 拉格朗日对偶函数

  凸优化问题：函数本身是二次的$(quadratic)$，函数的约束条件在其参数下是线性的，这样的函数称为凸优化问题。

  首先构造支持向量机的拉格朗日函数，也就是损失函数：$$L(\mathbf{w},b,\mathbf{\alpha })=\frac{1}{2}||\mathbf{w}|{|}^2+\sum _{i=1}^m{\alpha }_i(1-y_i({\mathbf{w}}^T{\mathbf{x}}_i+b))({\alpha }_i\ge 0)$$   其中，$\alpha =({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n{)}^T$。
  可以看出，拉格朗日函数分为两部分：第一部分和我们原始的损失函数一样，第二部分表达的是我们的约束条件。我们希望，构造的损失函数不仅能够代表我们原有的损失函数和约束条件，最好还能够表示我们想要最小化损失函数来求解$\mathbf{w}$和$b$的意图，所以我们要先以$\alpha$为参数，求解$L(\mathbf{w},b,\alpha )$的最大值，再以$\mathbf{w}$和$b$为参数，求解$L(\mathbf{w},b,\alpha )$的最小值。因此，我们的目标可以写作如下形式：$$\underset{\mathbf{w},b}{\min }\underset{{\alpha }_i\ge 0}{\max }L(\mathbf{w},b,\alpha )({\alpha }_i\ge 0)$$