分治算法(divide and conquer algorithm)是指把大问题分割成多个小问 题,然后把每个小问题分割成多个更小的问题,直到问题的规模小到能够 轻易解决。这种算法很适合用递归实现,因为把问题分割成多个与自身相 似的小问题正对应递归情况,当小问题已经达到了能够轻易解决的规模时, 遇到基本情况。分治算法所采用的解题策略有一项优势——并行地处理小 问题,这允许多个CPU (中央处理器)或多台计算机同时处理它们。
详细讲解见《递归算法与项目实战》第5章。(摘录部分内容)
第5章要讲解一些适合采用递归实现的分治算法,如二分搜索、快速排序 以及归并排序算法等。另外,我们还要重新考虑怎样对数组中的各整数求和,这次你会看到如何用 分治策略解决该问题。最后,第5章会介绍卡拉楚巴乘法算法,该算法为实现计算机硬件的快速乘法打下了基础。
1 二分搜索
假设书架上面有100本书。你并不记得每一本具体放在什么地方,但你知道这些书已经按 照书名字母顺序排列好。于是,在寻找 Zebras: The Complete Guide 这样的书时,你肯定不会从 头开始找,因为书架一开始摆放的应该是Aaron Burr Biography那种首字母靠前的书,你应该 在书架末尾的那些书中寻找才对。这本谈zebras的书未必是书架上的最后一本,因为它后面可 能还有名称以 zephyrs、zoos 或 zygotes 等词开头的书,尽管如此,但是它应该离书架末尾不太 远。我们可以把这样两个事实当作自己试探的基础(或者当作推理的线索),从而决定从末尾而 从不是开头寻找这本书。第一,书架上的书是按书名字母顺序排列的;第二,我们要找的这本 书的首字母为Z, 这样的书应该在书架的后一半,而不是前一半。
二分搜索 (binary search) 又称为二分查找,是一种通过反复将有序列表分成大致相等的 两半而从中搜索待查目标的方法。最公允的二分方式就是平分,也就是先查书架正中的那本 书,如果它不是你要找的书,那么接下来判断你要找的书是位于书架的前一半,还是位于书 架的后一半。
然后,你可以继续执行这个将有序列表分成大致相等的两半的操作,如图5-1 所示。也 就是说,你在刚才确定的那一半中,首先查看中间那本书,如果它不是你要找的书,那么接 下来判断你要找的书是在这个范围的前一半(也就是左侧),还是在这个范围的后一半(也就 是右侧),这样确定的范围大约相当于书架所有书数量的1/4。反复执行这一操作,直至找到你要找的书,如果你已经把这个范围缩小到0,但还没有找到自己要找的书,就可以宣布,这 本书不在书架上面。

图5-1 用二分搜索法反复将有序列表分成相等的两半,以便在其中寻找目标元素
这种搜索策略能够有效推广到更大规模的数据,因为即使图书的总量翻倍,整个搜索过 程也只会增加一步。假如用线性的(也就是一本一本的)搜索方式在摆放着50本书的书架上 寻找某一本书,那么最多有可能需要50步,在摆放着100本书的书架上寻找某一本书,最多 有可能需要100步。与之相比,用二分搜索法在摆放着50本书的书架上寻找某一本书,最多 只需要6步,在摆放着100本书的书架上寻找某一本书,最多只需要7步。
现在,我们把实现递归式的二分搜索算法时所要考虑的3个问题回答一遍。
- 什么是基本情况? 待搜索的范围长度为0的情况,或该范围中间的那个元素正好是待查 元素的情况。
- 在递归函数调用中应该传入什么样的参数? 传入接下来要搜索的这个范围的起止下标。
- 在递归函数调用中传入的参数是如何向基本情况靠近的?由于每次递归调用都会把搜 索范围变成原来的一半,因此最后该范围内总会出现只有一个元素的情况。如果这个元 素是我们要找的元素,那么二分搜索算法就遇到了其中一种基本情况,它会返回该元素 的位置;如果不是,那么下一次递归肯定会让待查范围的长度变为0,从而使二分搜索 算法遇到另一种基本情况,它会返回None, 以表示找不到该元素。
下面的 binarySearch.py程序中有一个binarySearch() 函数,它能够在haystack 参数表示的有序列表中搜索needle 参数表示的值。
关于《递归算法与项目实战》这本书

本书是写给那些害怕递归算法或对递归算法感兴趣的人的。对于程序员新手或计算机科学 专业大一的学生而言,递归好像是魔法。许多递归课程很难懂,这让许多人非常沮丧,甚至望 而生畏。对于这些读者,我希望本书直白的解读和大量的示例能让递归更容易理解。
要看懂本书,你必须会编写基本的 Python程序或 JavaScript 程序,因为正文中的示例代码 是用这两种语言编写的。本书中的代码去除了多余的部分,只保留了精华。你只要知道怎么创 建并调用函数,而且明白全局变量与局部变量有什么区别,就能够看懂书中的所有示例。
本书有14章。
第1部分包含第1~9章。
第1章解释什么叫递归,并说明编程语言中函数的实现方式与函数调用方式为什么会很自 然地形成递归。该章还会说明递归为什么不像想象中那样神奇。
第2章深入讨论递归与迭代的区别及相似之处。
第3章讲解经典的递归算法。
第4章讨论一种很适合用递归解决的问题,也就是树状结构的遍历问题,例如,当走迷宫 或浏览目录时,有可能需要做这样的遍历。
第5章讨论如何用递归把大问题拆分成多个小问题,并讲解常见的分治算法。
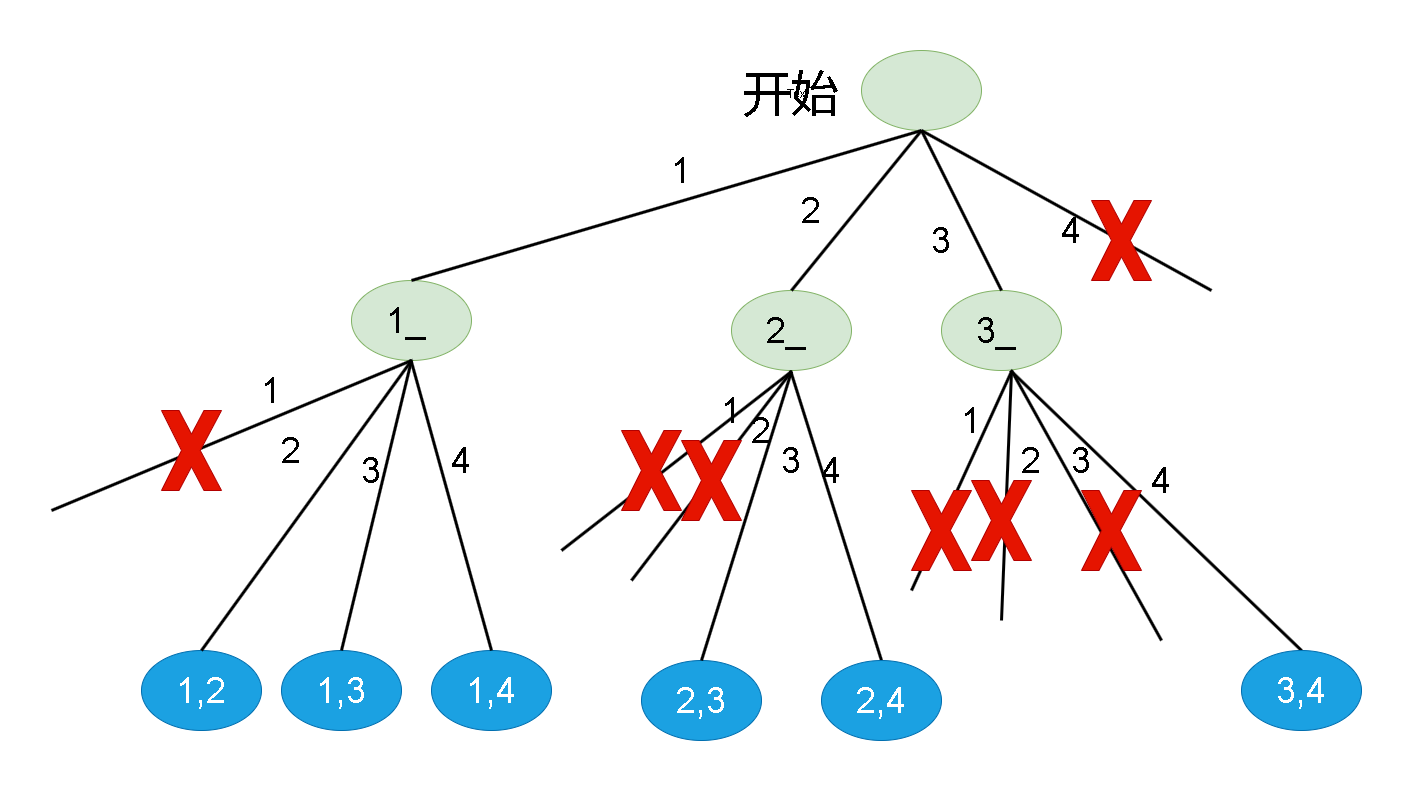
第6章讨论涉及排列与组合的递归算法,以及适合用这些算法解决的常见编程问题。
第7章讲解在用递归解决实际问题时提高编码效率的一些简单的技巧——记忆化与动态 规划。
第8章讲解尾调用优化及其原理。
第9章展示一些可以用递归算法绘制的图形。在该章中,我们使用 turtle 模块生成这些 图形。
第2部分包含第10~14章。
第10章介绍如何实现文件查找器项目,用于根据用户提供的搜索参数搜索计算机中的文件。
第11章讨论如何实现迷宫生成器项目——用递归回溯算法自动生成任意大小的迷宫。
第12章讲述如何实现滑块拼图项目,用于解决滑块拼图(这种拼图通常由15 个可以横竖 滑动的方块构成)问题。
第13章讨论如何实现分形图案制作器项目,生成指定的分形图案。
第14 章讨论如何实现画中画制作器项目:用 Pillow 这个图像操纵模块,生成递归式的画 中画效果。