【算法-数组3】螺旋数组（一入循环深似海啊！）

news2024/11/23 3:16:51

今天，带来数组相关算法的讲解。文中不足错漏之处望请斧正！

理论基础点这里

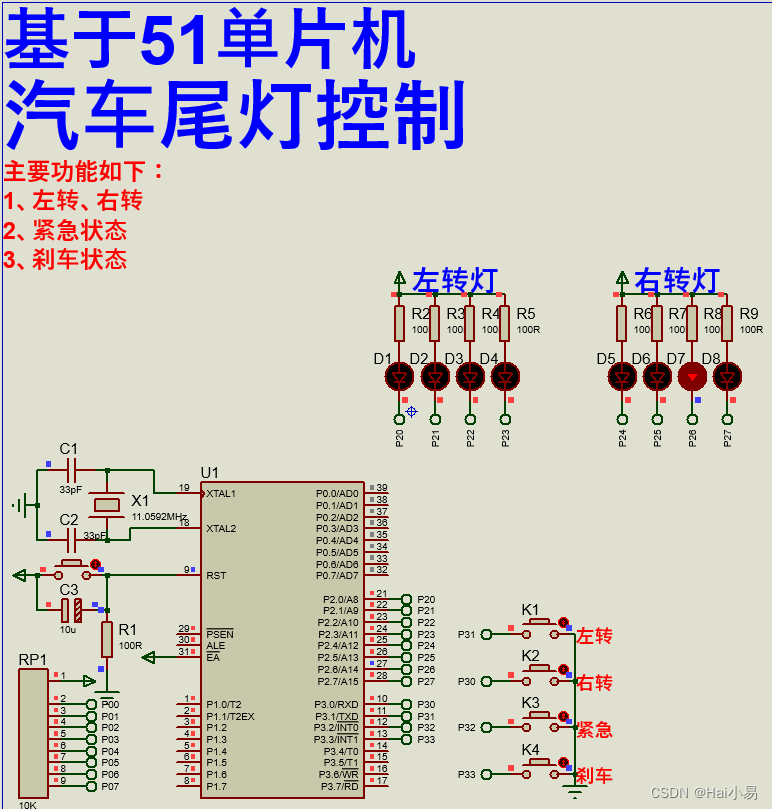
螺旋数组

1. 思路

这道题主要是模拟转圈过程，但是要处理的边界条件比较多，常见的问题就是每条边的处理都有自己的逻辑，那这就很难。如果不明确每条边该如何遍历，比如当n=5，上行填充5个元素，但是右列又只填充4个元素——每条边的区间不统一，就导致旋转起来很困难。即使第一圈转完了，第二圈也不知道如何向内走。

在二分搜索的时候，我们讲过循环不变量，这里也可以用上，来使循环变得清晰。

我们这里对每条边的处理，采用左闭右开的规则，即左闭右开的处理边界是循环不变量。
同时，我们对整个螺旋矩阵的生成拆分一下：

螺旋矩阵 = 按顺时针顺序旋转的一圈一圈递增的数字
每圈数字 = 上行（从左到右）的填充 + 右列（从上到下）的填充 + 下行（从右到左）的填充 + 左列（从下到上）的填充

在这里插入图片描述
如图中一样，将目标矩阵拆分，最终只需要重复最简单的“右上左下填充操作”就可以生成目标矩阵。

具体怎么走呢？

*我们表示元素的时候一般是nums[i][j]，i表示行的位置，j表示列的位置，所以等会遍历某一行的时候，元素nums[i][j]的列(j)在变化，循环变量用j；遍历某一列的时候，元素nums[i][j]的行(i)在变化，循环变量用i。

给startI代表行的起始位置，startJ代表列的起始位置，则

上行（遍历行，元素的列在变化）：j: [startJ -> n-1);
右列（遍历列，元素的行在变化）：i: [startI -> n-1);

图中：
startI = 0
startJ = 0
j: [startJ, n-1)
i: [startI, n-1)

下行（遍历行，元素的列在变化）：j: [j -> startJ)
- 由于向右走完，j已经为n-1，所以可以直接从j开始
左列（遍历列，元素的行在变化）：i: [i -> startI)
- 由于向下走完，i已经为n-1，所以可以直接从i开始

在这里插入图片描述
图中：

startI = 0
startJ = 0
i= n-1
j= n-1
j: [n-1, startJ)
i: [n-1, startI)

最外一圈走完了，那怎么往里面走呢？

其实只需要稍稍改动：走完一圈，要转的圈就缩小了，即下一圈的行是[startJ+1, n-2)，列同理。

左区间很简单，边转圈边增加startI和startJ，那右区间呢？不如我们直接默认给一个值为 n-1 的eleNum变量, 表示每次要填充的元素个数.

那我们转几圈呢？

n/2圈。因为每次转弯一圈，都是向最左列最右列、最上行最下行放置了元素。

那如果n是奇数呢？

就像我们图中画的一样，最后会剩下一个，我们在结尾特殊处理即可。

2. 参考代码

class Solution {
public:
    // 循环进行右下左上的填充操作
    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> matrix(n, vector<int>(n, 0));

        // 关于行列:
        // 1. 遍历行, 列属性变化 -- j移动
        // 2. 遍历列, 行属性变化 -- i移动
        int startI = 0; // i起始位置
        int startJ = 0; // j起始位置
        int eleNum = n - 1; // 每次要填充的元素个数
        int loopNum = n / 2; // 循环次数(奇数需要单独处理最后一个元素)
        int val = 1; // 要填充的值

        while (loopNum--) {
            int i = startI; // 某元素的行属性
            int j = startJ; // 某元素的列属性

            // 从左到右遍历行(列属性变化 -- j移动)
            for (j = startJ; j < eleNum; ++j) matrix[i][j] = val++;

            // 从上到下遍历列(行属性变化 -- i移动)
            for (i = startI; i < eleNum; ++i) matrix[i][j] = val++;

            // 从右到左遍历行(列属性变化 -- j移动)
            for (; j > startJ; --j) matrix[i][j] = val++;

            // 从下到上遍历列(行属性变化 -- i移动)
            for (; i > startI; --i) matrix[i][j] = val++;

            // 每次循环后, 需要填充的区间左右同时向中间缩一位
            // 行: [startJ, eleNum) --> [startJ+1, eleNum-1)
            // 列: [startI, eleNum) --> [startI+1, eleNum-1)
            ++startI;
            ++startJ;
            --eleNum; 
        }

        //  当 n 为奇数, 矩形中间会留下一个没处理的
        if (n % 2 != 0) matrix[n / 2][n / 2] = val;

        return matrix;
    }
};