目录
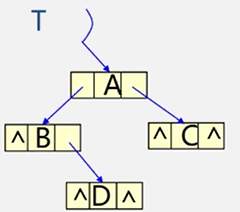
二叉搜索树又叫二叉排序树,它具有以下特征
二次搜索树的效率
模拟最简二叉搜索树代码
代码片段分析
查找二叉搜索树数据:
如果我们用递归的方法查找数据有什么不一样?
插入数据
删除数据(难点)
二叉搜索树又叫二叉排序树,它具有以下特征
1.左子树 不为空 的时候 左子树上的所有节点 比 根节点 小
2.右子树 不为空 的时候 右子树上的所有节点 比 根节点 大
3.每棵分树仍然是 二叉搜索树

二次搜索树的效率
可以看到如果在使用二叉搜索树查找数据时效率非常高,如查找图中数据60时直接将左树数据排除
一下排除了一半的数据
二叉搜索树的最优形态为完全二叉树:O(log2n)
二叉搜索树的最差形态为单支树:O(n)
为了避免二叉搜索树变成单分支树我们通过左旋右旋的方式将单分支树变为AVL树入:


为减少AVL树左旋右旋次数就加入颜色变为红黑树
模拟最简二叉搜索树代码
public class MyBinarySearchTree {
static class Node{
int val;
Node left;
Node right;
public Node(int val){
this.val = val;
}
}
// 二叉搜索树 根节点
Node root = null;
private int size;
// 插入数据
public void put(int val){
// 查看二叉搜索树是否为空
// 实例化一个节点
Node node = new Node(val);
if(root == null){
root = node;
return;
}
// 二叉搜索树插入到叶子节点
Node cur = root;
Node curFather = null;
while(cur != null){
if(val > cur.val){
curFather = cur;
cur = cur.right;
}else if(val < cur.val){
curFather = cur;
cur = cur.left;
}else{
// 二叉搜索树只用来 查找,
// 所以遇到相同的值时说明二叉搜索树已经存有,查找时也能查到就无需将重复的数据插入进去了
System.out.println("二叉搜索树已经存有该数据: "+ val+" 无需继续存储就去");
return;
}
}
//出了这个循环说明cur已经到了最后null,curFather节点指向二次搜索树叶子节点
if(val > curFather.val){
curFather.right = node;
size++;
}else{
curFather.left = node;
size++;
}
}
// 中序遍历
private Node inordercur = root;
public void inorder(Node inordercur){
if(inordercur == null){
return;
}
inorder(inordercur.left);
System.out.print(inordercur.val+" ");
inorder(inordercur.right);
}
// 查找二叉搜索树
public Node find(int val){
Node cur = root;
// // 判断根节点是否为空
// if(cur == null){
// System.out.println("搜索二叉树节点为空,无法查找");
// return null;
// }
while(cur != null){
if(val > cur.val){
cur = cur.right;
}else if(val < cur.val){
cur = cur.left;
}else{
// 找到相等值
return cur;
}
}
// 出了此循环说明cur为null,说明查找到数据
System.out.println("没有查找到: "+ val );
return null;
}
// 查找二叉搜索树方法2
private Node find2(int val,Node root){
if(root == null){
return null;
}
if(val == root.val){
return root;
}
Node leftNode = find2(val,root.left);
if(leftNode != null){
return leftNode;
}
Node rightNode = find2(val,root.right);
if(rightNode != null){
return rightNode;
}
return null;
}
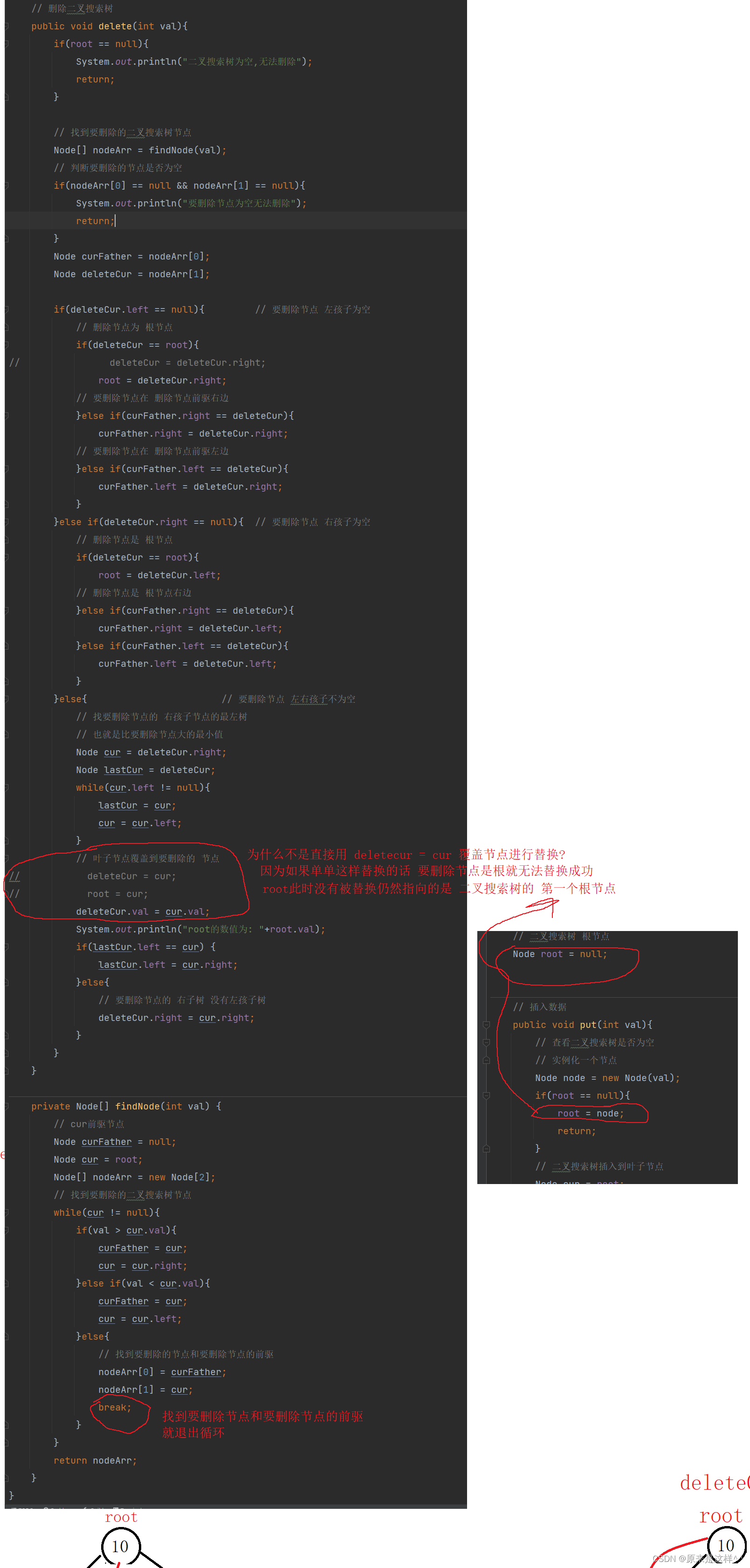
// 删除二叉搜索树
public void delete(int val){
if(root == null){
System.out.println("二叉搜索树为空,无法删除");
return;
}
// 找到要删除的二叉搜索树节点
Node[] nodeArr = findNode(val);
// 判断要删除的节点是否为空
if(nodeArr[0] == null && nodeArr[1] == null){
System.out.println("要删除节点为空无法删除");
return;
}
Node curFather = nodeArr[0];
Node deleteCur = nodeArr[1];
if(deleteCur.left == null){ // 要删除节点 左孩子为空
// 删除节点为 根节点
if(deleteCur == root){
// deleteCur = deleteCur.right;
root = deleteCur.right;
// 要删除节点在 删除节点前驱右边
}else if(curFather.right == deleteCur){
curFather.right = deleteCur.right;
// 要删除节点在 删除节点前驱左边
}else if(curFather.left == deleteCur){
curFather.left = deleteCur.right;
}
}else if(deleteCur.right == null){ // 要删除节点 右孩子为空
// 删除节点是 根节点
if(deleteCur == root){
root = deleteCur.left;
// 删除节点是 根节点右边
}else if(curFather.right == deleteCur){
curFather.right = deleteCur.left;
}else if(curFather.left == deleteCur){
curFather.left = deleteCur.left;
}
}else{ // 要删除节点 左右孩子不为空
// 找要删除节点的 右孩子节点的最左树
// 也就是比要删除节点大的最小值
Node cur = deleteCur.right;
Node lastCur = deleteCur;
while(cur.left != null){
lastCur = cur;
cur = cur.left;
}
// 叶子节点覆盖到要删除的 节点
// deleteCur = cur;
// root = cur;
deleteCur.val = cur.val;
System.out.println("root的数值为: "+root.val);
if(lastCur.left == cur) {
lastCur.left = cur.right;
}else{
// 要删除节点的 右子树 没有左孩子树
deleteCur.right = cur.right;
}
}
}
private Node[] findNode(int val) {
// cur前驱节点
Node curFather = null;
Node cur = root;
Node[] nodeArr = new Node[2];
// 找到要删除的二叉搜索树节点
while(cur != null){
if(val > cur.val){
curFather = cur;
cur = cur.right;
}else if(val < cur.val){
curFather = cur;
cur = cur.left;
}else{
// 找到要删除的节点和要删除节点的前驱
nodeArr[0] = curFather;
nodeArr[1] = cur;
break;
}
}
return nodeArr;
}
}
代码片段分析
初始化:一个二叉搜索树底层仍然是一颗二叉树,每个树有3个域,分别是值域val,左树地址域,右树地址域,一棵二叉搜索树有一个根节点

查找二叉搜索树数据:
方法参数为想要查找的数据值
如果根节点不为空的话
查找数据val > 根节点的话就往右树找 cur = cur.right
查找数据val < 根节点的话就往左树找 cur = cur.left
查找到数据val = 根节点的话就直接返回此节点,说明找到了
根节点为null或出了循环仍然未找到说明二叉搜索树里没有这个值,返回null

如果我们用递归的方法查找数据有什么不一样?
我们可以发现如果用递归写的话我们就无法用到二叉搜索树的优点,它还是将每个节点查找一次,时间复杂度比较高

插入数据
将数据插入到二叉搜索树里就是将数据插到树的叶子节点
方法参数为想要插入的数据
1.首先根据数据先实例化一个节点
2.判断是否为空,为空的话说明此时插入的节点为二叉搜索树的第一个节点,将新的节点赋值为根节点
3.找到要插入对应的叶子节点位置
3.1:插入数据 > 根节点,往右树走
3.2:插入数据 < 根节点,往左树走
3.3:如果插入数据 = 根节点,退出(因为二叉搜索树是用来查找数据是否存在的,因此只要有一个数据在那就行了)
4.记得放一个父亲节点curFather跟在cur节点后面,当cur循环结束后说明cur节点此时为null,而curFather父亲节点刚好就在最后的叶子位置
5.要插入节点 > curFather叶子节点: curFather.right = 要插入节点
要插入节点 < curFather叶子节点: curFather.left = 要插入节点

删除数据(难点)
1.判断根节点是否为null,是null直接返回无法删除
2.找到要删除节点和要删除节点的前驱
3.要删除节点的左子树为空时
3.1:要删除节点刚好是根节点且左树为空:
根节点移到要删除节点右边: root = deleteCur.right
3.2:要删除节点不是根节点且左树为空:
根节点的左树移到要删除节点的右边
4.要删除节点的右子树为空时
4.1:要删除节点刚好是根节点且右子树为空
根节点移到要删除节点左边: root = deleteCur.left

4.2要删除节点不是跟节点且右树为空
root根节点的左树指向要删除节点的左树: root.left = deleteCur.left
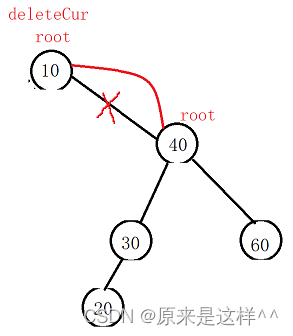
5.要删除节点左子树和右子树都不为null(最难点)
1.找要删除的节点和要删除节点的前驱
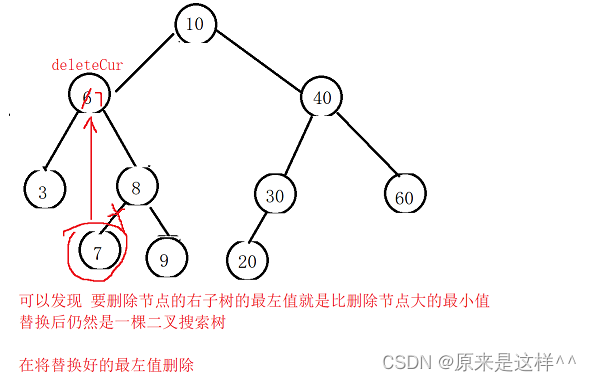
2.找到要删除节点右子树的最左树 或 要删除节点的左子树的最右树
要删除节点右子树的最左树就是比删除节点大的最小值
要删除节点的左子树的最右树就是比删除节点小的最大值
3.替换,
4.将替换后的最左树或最右树删除,删除完毕后可以发现它仍然是一棵 二叉搜索树
5.如果要删除节点的右子树没有最左边 或 要删除节点的左子树没有最右边 怎么办
5.1:还是先替换,将要删除的节点进行覆盖删除
5.2:将要删除节点的右孩子树移到cur的右孩子树中,这样替换后的节点就会被删除