题目： 

有一个含1~n的n个整数序列a，通过一个栈可以产生多种出栈序列，设计一个算法采用链栈判断序列b（为1~n的某个排列）是否为一个合适的出栈序列，并用相关数据进行测试。

解释： 

①栈空，a[O]进栈（i=1)；6[0]≠栈顶元素，a[1]进栈（i=2)；b[0]≠栈顶元素，a[2]
进栈(i=3），如图3.13(a）所示。

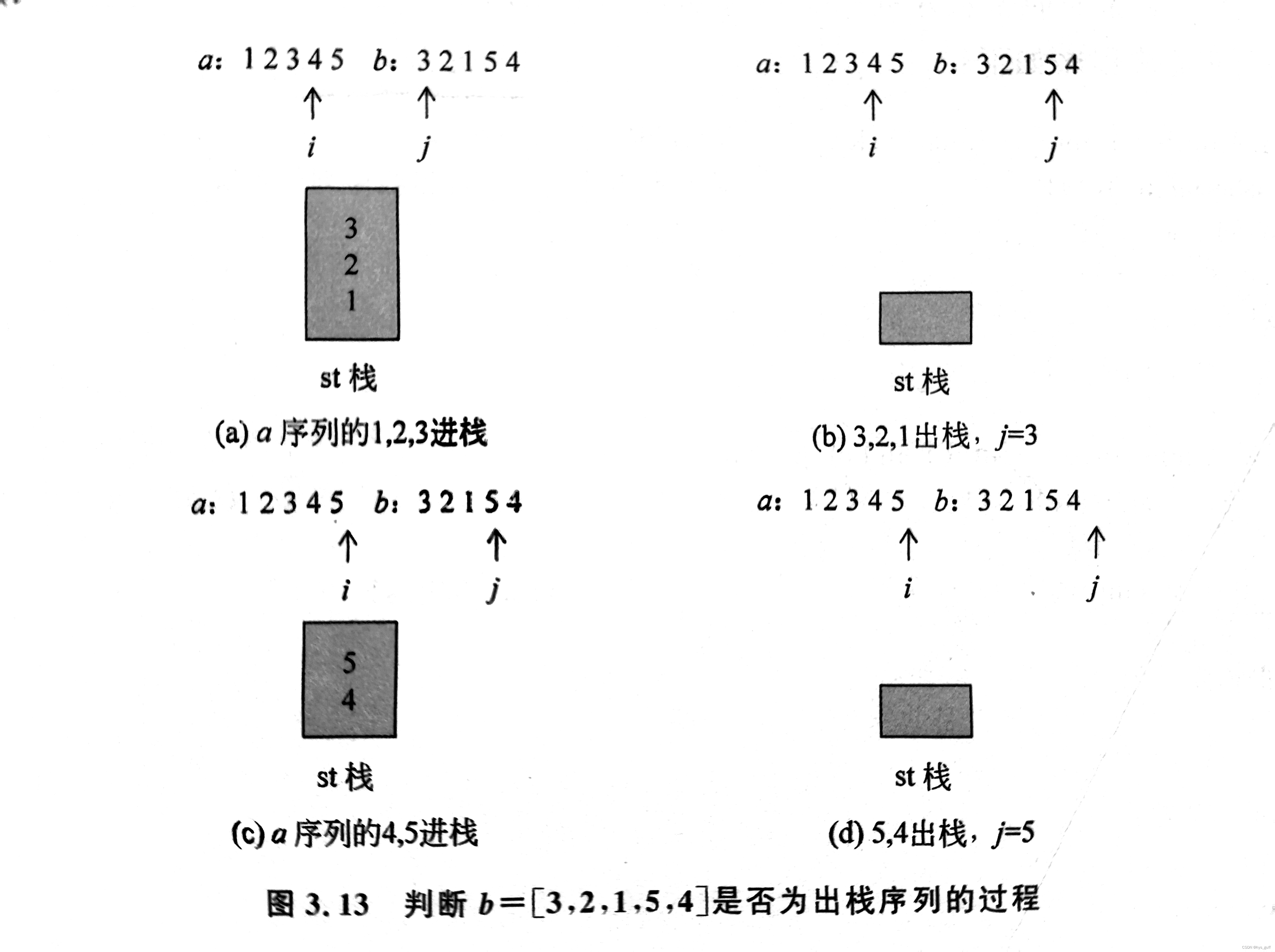
②b[0]=栈顶元素，出栈一次，j增1（j=1)；6[1]=栈顶元素，出栈一次，j增1(j=2);
b[2]=栈顶元素，出栈一次，j增1(j=3)，如图3.13（b)所示。
③栈空，a[3]进栈(i=1)；b[3]≠栈顶元素，a[3]进栈(i=4)；6[3]≠栈顶元素，a[4]
进栈（i=5,a序列遍历完毕），如图3.13(c）所示。
④ b[3]=栈顶元素，出栈一次，j增1(j=4)；6[4]=栈顶元素，出栈一次，j增1(j=5),
如图3.13（d)所示。
此时a序列遍历完毕，栈空返回True，表示6序列是a序列的出栈序列。
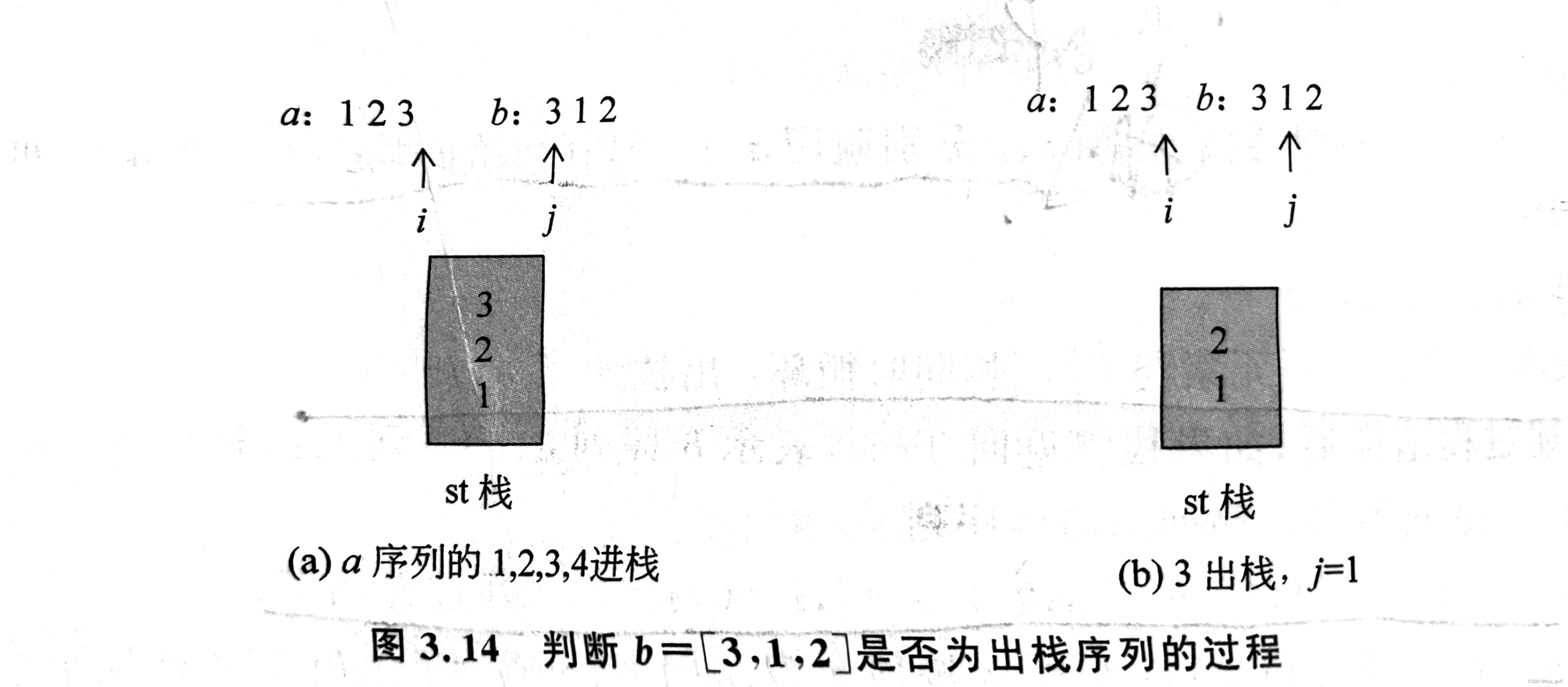
又例如，a=[1,2,3],6=[3,1,2],i=0，j=0，判断过程如下：
① 栈空，a[O]进栈（i=1)；b[O]≠栈顶元素，a[1]进栈（i=2)；6[O]≠栈顶元素，a[2]
进栈(i=3,a序列遍历完毕），如图3.14(a)所示。
② 6[O]=栈顶元素，出栈一次，j增1（j=1)；6[1]≠栈顶元素，如图3.14（b)所示。

代码：

# 判断出栈顺序是否合法
def is_Serial(a,b,n):       #a,b为栈，n为个数
    st=LinkStack()             #创建一个栈空间
    i,j=0,0
    while i<n:
        st.push(a[i])
        i+=1
        while not st.is_empty() and st.gettop()==b[j]:      #相同就弹出，有时该while循环循环多次
            st.pop()
            j+=1
    return st.is_empty()        #按循序抵消直到栈空，若有未消掉的元素，则顺序不合法
a=[1,2,3,4]
b=[1,3,2,4]
c=[4,2,3,1]
print(is_Serial(a,b,4))
print(is_Serial(a,c,4))