第六章 树【数据结构和算法】【精致版】
- 前言
- 版权
- 第六章 树
- 6.1 应用实例
- 6.2 树的概念
- 6.2.1树的定义与表示
- 6.2.2 树的基本术语
- 6.2.3树的抽象数据类型定义
- 6.3 二叉树
- 6.3.1二叉树的定义
- 6.3.2 二叉树的性质
- 6.3.3 二叉树的存储
- 6.4 二叉树的遍历
- 6.4.1 二叉树的遍历及递归实现
- **1-二叉树的递归实现.c**
- 6.4.2 二叉树遍历的非递归实现
- **2-二叉树的非递归实现.c**
- 6.4.3 遍历算法的应用
- **3-二叉树的遍历算法应用.c**
- 6.4.4由遍历序列确定二叉树
- 6.5线索二叉树
- 6.5.1 线索二叉树的基本概念
- 6.5.2 二叉树的线索化
- 6.5.3 线索二叉树的遍历
- 6.6 树和森林
- 6.6.1 树的存储
- 6.6.2 树、森林与二叉树的转换
- 6.6.3 树和森林的遍历
- 6.7哈夫曼树及其应用
- 6.7.1哈夫曼树
- 6.7.2哈夫曼编译码
- 6.8 实例分析与实现
- 6.8.1表达式树
- 6.8.2树与等价类的划分
- 6.8.3回溯法与N皇后问题
- 6.9 算法总结
- 实验
- 哈夫曼编码的实现
- 习题
- 1.单项选择题
- 3.完成题
- 4.算法设计题
- (1)编写算法,在以二叉链表存储的二叉树中,求度为2的结点的个数。
- (2)编写算法,在以二叉链表存储的二叉树中,交换二叉树各结点的左右子树。
- 最后
前言
2023-11-6 16:22:17
以下内容源自《【数据结构和算法】【精致版】》
仅供学习交流使用
版权
禁止其他平台发布时删除以下此话
本文首次发布于CSDN平台
作者是CSDN@日星月云
博客主页是https://jsss-1.blog.csdn.net
禁止其他平台发布时删除以上此话
第六章 树
6.1 应用实例
- 数据压缩问题
- 表达式的树形表示
- 等价类划分问题
6.2 树的概念
6.2.1树的定义与表示
1.树的定义
树(tree)是n(n≥0)个结点的有限集合。当n=0时,称为“空树”;当n>0时,该集合满足如下条件。
①有且仅有一个称为“根"(root)的特定结点,该结点没有前驱结点,但有零个或多个直接后继结点。
②除根结点之外的n-1个结点可划分成m(m≥0)个互不相交的有限集T1,T2,T3,…,Tn,
每个Ti又是一棵树,称为“根的子树”(subtree)。每棵子树的根结点有且仅有一个直接前驱就是树的根结点,同时可以有零个或多个直接后继结点。
树的定义采用了递归定义的方法,即树的定义中又用到了树的概念,这正好反映了树的特性。
2.树的表示方法
①树形图表示
②嵌套集合表示法(文氏图表示法)
③广义表表示法(嵌套括号表示法)
④凹入表示法
6.2.2 树的基本术语
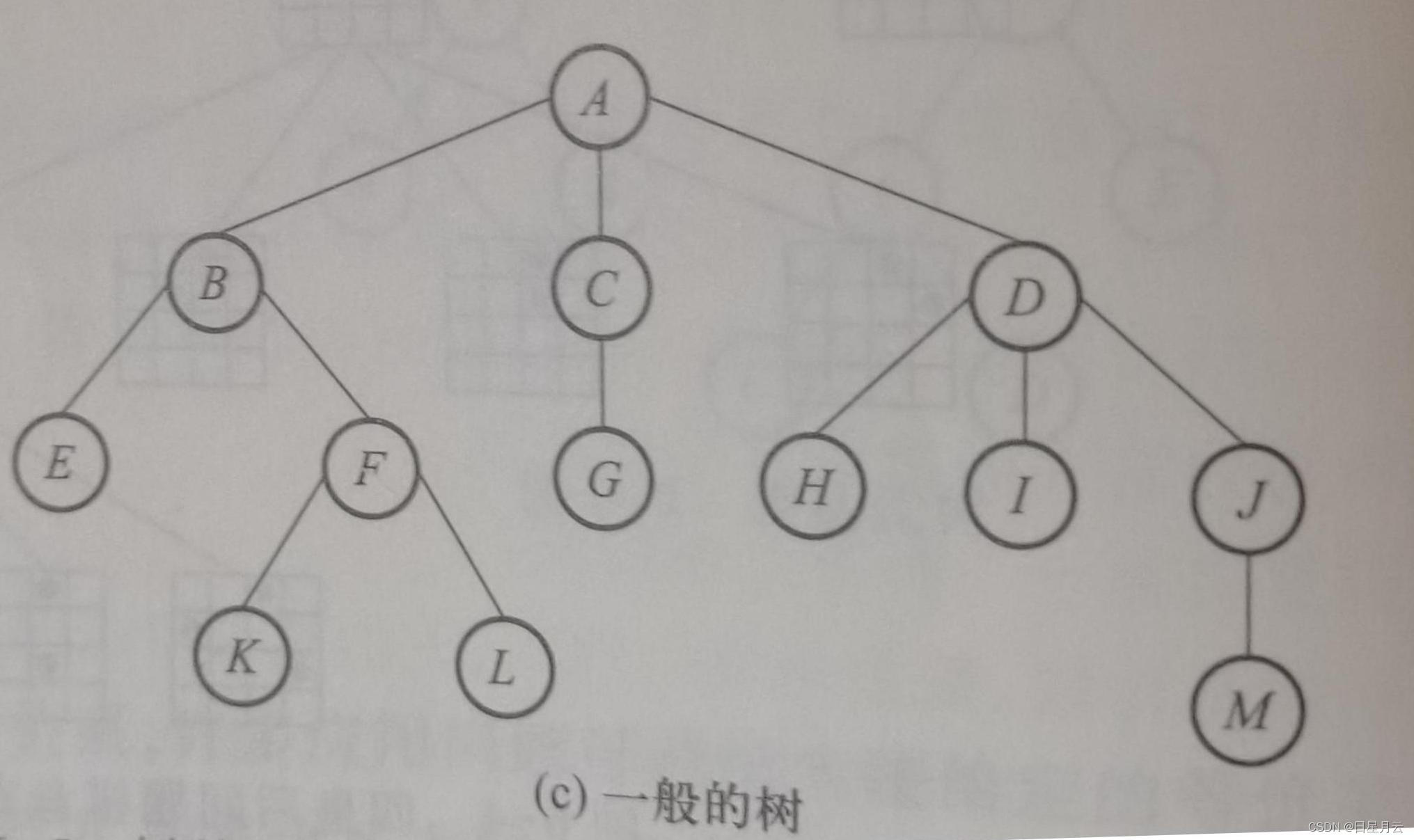
以下列出一些有关树的基本术语。
结点(node):包含一个数据元素及若干指向其子树的分支。如图6-5©中的树有A、B、C、 D、E等13个结点。
结点的度(degree):结点拥有子树的个数称为该结点的“度”。如图6-5©中结点A的度为3,结点B的度为2.
树的度:树中所有结点的度的最大值。如图6-5( c )树的度为3。
叶子结点(leaf):度为0的结点称为“叶子结点”,也称“终端结点”。如图6-5©中结点E、 K、L.G等均为叶子结点。
内部结点(internal node):度不为0的结点称为“内部结点”,也称为“分支结点”或“非终端结点”。如图6-5( c )中结点B、C、D等均为内部结点
下面借助人类族谱的一些术语描述树中结点之间的关系,以便直观理解
孩子结点(child):结点的子树的根(即直接后继)称为该结点的“孩子结点”。如图6-5© 中结点B、C、D是A结点的孩子结点,结点E、F是B结点的孩子结点。
双亲结点(parent):结点是其子树的根的双亲,即结点是其孩子的双亲。如图6-5©中结 点A是B、C、D的双亲结点,结点D是H、I、J的双亲结点。
兄弟结点(sibling):同一双亲的孩子结点之间互称兄弟结点。如图6-5©中结点H、I、J互 为兄弟结点。
堂兄弟:双亲是兄弟或堂兄弟的结点间互称堂兄弟结点。如图6-5©中结点E、G、H互为 堂兄弟,结点L、M也互为堂兄弟。
祖先结点(ancestor):结点的祖先结点是指从根结点到该结点的路径上的所有结点。如图 6-5©中结点K的祖先是A、B、F结点。
子孙结点(descendant):结点的子孙结点是指该结点的子树中的所有结点。 结点D的子孙有H、1、J、M结点
结点的层次(level):结点的层次从树根开始定义,根为第一层,根的孩子为第二层。若某 点在第系层,则其孩子就在第k+1层,以此米推。如图6-5©中结点C在第二层,结点M在 四层
树的深度(deph):树中所有结点层次的最大值称为树的“深度”,也称树的“高度”。如果 6-5©中的树的深度为4。
前辈:层号比某结点层号小的结点,都可称为该结点的“前辈”。如图6-5©中结点A、B C、D都可称为结点E的前辈。
后辈:层号比某结点层号大的结点,都可称为该结点的“后辈”。如图6-5©中结点K、L 都可称为结点E的后辈
森林(forest):m(m=0)棵互不相交的树的集合称为“森林”。在数据结构中,树和森林不像自然界中有明显的量的差别,可以称0棵树、1棵树为森林。任意一棵非空的树,删去根结点变成了森林;反之,给森林中各棵树增加一个统一的根结点,就变成了一棵树
有序树(ordered tree)和无序树(unordered tree):树中结点的各棵子树从左到右是有特定次序的树称为“有序树”,否则称为“无序树”。
6.2.3树的抽象数据类型定义
略
6.3 二叉树
6.3.1二叉树的定义
二叉树(binary tree)是n(n20)个结点的有限集合。当n时,称为“空二叉树”;当n>( 时,该集合由一个根结点及两棵互不相交的,被分别称为“左子树”和“右子树”的二叉树 组成。
以前面定义的树为基础,二叉树可 以理解为是满足以下两个条件的树形结构
① 每个结点的度不大于2。
② 结点每棵子树的位置是明确区分左右的,不能随意改变。
由上述定义可以看出:二叉树中的每个结点只能有0、1或2个孩子,而且孩子有左右之分, 即使仅有一个孩子,也必须区分左右。位于左边的孩子(或子树)叫左孩子(左子树),位于右边 的孩子(或子树)叫右孩子(右子树)。
二叉树也是树形结构,故6.2.2小节所介绍的有关树的术语都适用于二叉树。
二叉树不是结点度不大于2的有序树,
反例:只有右子树的二叉树和只有左子树的二叉树不同
6.3.2 二叉树的性质
- 在二叉树的第i层上至多有2i-1个结点(i>=1)
- 深度为k的二叉树至多有2k-1个结点(k>=1)
- 对于任意一颗二叉树T,若终端结点数为n0,度为2的结点数为n2,则n0=n2+1.
下面给出两种特殊的二叉树,然后讨论其相关性质。
满二叉树 深度为k且含有2k-1个结占的一叉树称为“满二叉树”
满二叉树的连续编号:对含有n个结点的的满二叉树,约定从根开始,按层从上到下,每
层内从左到右,逐个对每一结点进行编号1,2,…,n。
完全二叉树 深度为k、结点数为n(n<=2k-1)的二叉树,当且仅当其n个结点与满二叉树
中连续编号为1至n的结点位置一一对应时,称为“完全二叉树”。
完全二叉树有两个重要特征:其一,所有叶子结点只可能出现在层号最大的两层上;其二,对
任意结点,若其右子树的层高为k,则其左子树的层高只可为k或k+1。
由定义可知,满二叉树必为完全二叉树,而完全二叉树不一定是满二叉树。
-
具有n个结点的完全二叉树的深度为[log2n」+1。向下取整
-
对于具有n个结点的完全二叉树,如果按照对满二义树结点进行连续编号的方式,
对所有结点从1开始顺序编号,则对于任意序号为的结点有以下结论。
① 如果i=1,则结点i为根,其无双亲结点;如果i>1,则结点i,则结点i的双亲结点为[i/2] 向下取整
② 如果2i<=n,则结点i的左孩子结点序号为2i,否则,结点i无左孩子。
③ 如果2i+1<=n,则结点i的右孩子结点序号为2i+1,否则,结点i无右孩子。
6.3.3 二叉树的存储
1.顺序存储结构
对于满二叉树和完全二叉树来说,可以按照对满二叉树结点连续编号的次序,将各结点数据
存放到一组连续的存储单元中,即用一维数组作存储结构,将二又树中编号为i的结点存放在数
组的第i号分量中、根据二叉树的性质5,可知数组中下标为i的结点的左孩子下标为2i,右孩
子下标为2i+1,双亲结点的下标为[ i/2」。
二叉树的顺序存储结构可描述如下。
#define MAX 100
typedef struct{
datatype SqBiTree[ MAX+1]; //0号单元不用
int nodemax; //数组中最后一个结点的下标
}Bitree;
2.链式存储结构
二叉树的二叉链表结点结构:
LChild域指向该结点的左孩子
Data域指向该结点的数据
RChild域指向该结点的右孩子
typedef char DataType;
typedef struct Node{
DataType data;
struct Node * LChild;
struct Node * RChild;
}BiTNode,*BiTree;
一个二叉树含有n个结点,则它的二叉链表中必含有2n个指针域,而仅有n-1个指针域指向其孩子,其余的n+1的指针域为空的链域。
可以用空链域存储其他有用的信息,便得到“线索二叉树”
二叉树的三叉链表结点结构:
Parent域指向该结点的双亲
LChild域指向该结点的左孩子
Data域指向该结点的数据
RChild域指向该结点的右孩子
6.4 二叉树的遍历
6.4.1 二叉树的遍历及递归实现
1.二叉树的遍历
依据对根结点访问的先后次序不同来命名二叉树的访问方式,分别称DLR为先序遍历(或
先根遍历)、LDR为中序遍历(或中根遍历),LRD为后序遍历(或后根遍历)
下面给出二叉树三种遍历方式的递归定义。
(1)先序遍历
其二叉树为空,则空操作;否则依次执行如下二个操作,
①访问根结点。
②按先序遍历左子树。
③按先序遍历右子树。
(2)中序遍历
若二叉树为空,则空操作;否则依次执行如下三个操作。
①按中序遍历左子树。
②访问根结点。
③按中序遍历右子树。
(3)后序遍历
若二叉树为空,则空操作;否则依次执行如下三个操作。
①按后序遍历左子树。
②遍历右子树。
③访问根结点。
2.二叉树遍历的递归实现
1-二叉树的递归实现.c
#include<stdio.h>
#include<stdlib.h>
typedef char DataType;
typedef struct Node{
DataType data;
struct Node * LChild;
struct Node * RChild;
}BiTNode,*BiTree;
#define FALSE 0
#define TRUE 1
#define MAXSIZE 10
//【算法6-17】用扩展先序遍历序列创建二叉链表
void CreateBiTree( BiTree *root){
char ch;
ch=getchar();
if(ch=='^') * root= NULL;
else{
* root = (BiTree) malloc(sizeof(BiTNode));
(*root)->data=ch;
CreateBiTree(&((*root)->LChild));
/*以左子树域地址为参数,可使被调用函数中建立的结点指针置于该域中*/
CreateBiTree(&((*root)->RChild));
/*以右子树域地址为参数,可使被调用函数中建立的结点指针置于该域中*/
}
}
//访问
void Visit(DataType n){
printf("%c",n);
}
//【算法6-1】递归 先序
void PreOrder(BiTree root){
//先序遍历二叉树,root为根节点的指针
if(root){
Visit(root->data);
PreOrder(root->LChild);
PreOrder(root->RChild);
}
}
//【算法6-2】递归 中序
void InOrder(BiTree root){
//中序遍历二叉树,root为根节点的指针
if(root){
InOrder(root->LChild);
Visit(root->data);
InOrder(root->RChild);
}
}
//【算法6-3】递归 后序
void PostOrder(BiTree root){
//后序遍历二叉树,root为结点的指针
if(root){
PostOrder(root->LChild);
PostOrder(root->RChild);
Visit(root->data);
}
}
//ABD^G^^^CE^H^^F^^
int main(){
BiTree root;
BiTree *_root=&root;
printf("输入扩展先序序列\n");
//ABD^G^^^CE^H^^F^^
CreateBiTree(_root);
printf("先序序列(递归)\n");
PreOrder(root);//ABDGCEHF
printf("\n");
printf("中序序列(递归)\n");
InOrder(root);//DGBAEHCF
printf("\n");
printf("后序序列(递归)\n");
PostOrder(root);//GDBHEFCA
printf("\n");
}
6.4.2 二叉树遍历的非递归实现
1.先序遍历二叉树的非递归实现
2.中序遍历二叉树的非递归实现
3.后序遍历二叉树的非递归实现
4.二叉树的层次遍历
2-二叉树的非递归实现.c
#include<stdio.h>
#include<stdlib.h>
typedef char DataType;
typedef struct Node{
DataType data;
struct Node * LChild;
struct Node * RChild;
}BiTNode,*BiTree;
//定义顺序栈
#define MAXSIZE 10
typedef BiTree ElemType;
typedef struct{
ElemType elem[MAXSIZE];
int top;
}SeqStack;
//(1)置空栈
//首先建立栈空间,然后初始化栈顶指针。
SeqStack * InitStack(){
SeqStack *s;
s=(SeqStack * ) malloc(sizeof( SeqStack));
s->top=-1;
return s;
}
//(2)判空栈
int Empty(SeqStack *s){
if(s->top==-1) return 1; //代表空
else return 0;
}
//(3)入栈
int Push(SeqStack *s, ElemType x){
if(s->top==MAXSIZE-1) return 0;//栈满不能入栈,否则将造成“上溢”
else {
s->top++;
s->elem[s->top]=x;
return 1;
}
}
//(4)出栈
int Pop( SeqStack *s, ElemType *x){
if(Empty(s)) return 0; //栈空不能出栈
else {
*x=s->elem[s->top];//栈顶元素存入*x,返回
s->top--;
return 1;
}
}
//(5)取栈顶元素
ElemType GetTop(SeqStack *s){
if(Empty(s)) return 0;//栈空
else return (s->elem[s->top]);
}
#define FALSE 0
#define TRUE 1
#define MAXSIZE 10
typedef BiTree QueueDataType;
//链队列的数据类型描述如下。
typedef struct node{
QueueDataType data;
struct node * next;
}QNode;
//链队列结点的类型
typedef struct{
QNode * front;
QNode * rear;
} LQueue;//将头尾指针封装在一起的链队列
//(1)创建一个带头结点的空队
LQueue * Init_LQueue(){
LQueue *q; QNode*p;
q=(LQueue*)malloc( sizeof(LQueue));//申请头尾指针结点
p=(QNode*)malloc( sizeof(QNode));//申请链队列头结点
p->next=NULL;
q->front=q->rear=p;
return q;
}
//(2)入队
void InLQueue(LQueue *q , QueueDataType x){
QNode *p;
p=(QNode*)malloc(sizeof(QNode));//申请新结点
p->data=x;
p->next=NULL;
q->rear->next=p;
q->rear=p;
}
//(3)判队空
int Empty_LQueue(LQueue *q){
if(q->front==q->rear) return 1;//代表空
else return 0;
}
//(4)出队
int Out_LQueue(LQueue *q, QueueDataType *x){
QNode *p;
if(Empty_LQueue(q)){
printf("队空");
return FALSE;
}
else{
p=q->front->next;
q->front->next=p->next;
*x=p->data;//队头元素放x中
free(p);
if(q->front->next==NULL)//只有一个元素时,出队后队空,修改队尾指针
q->rear=q->front;
return TRUE;
}
}
//【算法6-17】用扩展先序遍历序列创建二叉链表
void CreateBiTree( BiTree *root){
char ch;
ch=getchar();
if(ch=='^') * root= NULL;
else{
* root = (BiTree) malloc(sizeof(BiTNode));
(*root)->data=ch;
CreateBiTree(&((*root)->LChild));
/*以左子树域地址为参数,可使被调用函数中建立的结点指针置于该域中*/
CreateBiTree(&((*root)->RChild));
/*以右子树域地址为参数,可使被调用函数中建立的结点指针置于该域中*/
}
}
//访问
void Visit(DataType n){
printf("%c",n);
}
//【算法6-4】非递归 先序
void PreOrderN(BiTree root){
SeqStack *S;
BiTree p;
S=InitStack();
p=root;
while(p!=NULL||!Empty(S)){//当前结点指针及栈均空,则结束
while (p!=NULL){//访问根结点,根指针进栈,进入左子树
Visit(p->data);
Push(S,p);
p=p->LChild;
}
if(!Empty(S)){//根指针退栈,进入其右子树
Pop(S,&p);
p=p->RChild;
}
}
}
//【算法6-5】非递归 中序-1
void InOrderN1(BiTree root){
SeqStack *S;
BiTree p;
S=InitStack();
p=root;
while(p!=NULL||!Empty(S)){//当前结点指针及栈均空,则结束
while (p!=NULL){//访问根结点,根指针进栈,进入左子树
Push(S,p);
p=p->LChild;
}
if(!Empty(S)){//根指针退栈,进入其右子树
Pop(S,&p);
Visit(p->data);
p=p->RChild;
}
}
}
//【算法6-6】非递归 中序-2
void InOrderN2(BiTree root){
SeqStack *S;
BiTree p;
S=InitStack();
p=root;
while(p!=NULL||!Empty(S)){//当前结点指针及栈均空,则结束
if (p!=NULL){//访问根结点,根指针进栈,进入左子树
Push(S,p);
p=p->LChild;
}else{//根指针退栈,进入其右子树
Pop(S,&p);
Visit(p->data);
p=p->RChild;
}
}
}
//【算法6-7】非递归 后序
void PostOrderN(BiTree root){
SeqStack *S;
BiTree p,q;
S=InitStack();
p=root;
q=NULL;
while(p!=NULL||!Empty(S)){//当前结点指针及栈均空,则结束
while (p!=NULL){//访问根结点,根指针进栈,进入左子树
Push(S,p);
p=p->LChild;
}
if(!Empty(S)){
p=GetTop(S);
if((p->RChild==NULL)||(p->RChild==q)){
//判断栈顶结点的有子树是否为空,右子树是否刚访问过
Pop(S,&p);
Visit(p->data);
q=p;
p=NULL;
}else{
p=p->RChild;
}
}
}
}
//【算法6-8】二叉树的层次遍历
void LevelOrder(BiTree root){
LQueue *Q;
BiTree p;
Q=Init_LQueue();
InLQueue(Q,root);
while(!Empty_LQueue(Q)){
Out_LQueue(Q,&p);
Visit(p->data);
if(p->LChild!=NULL){
InLQueue(Q,p->LChild);
}
if(p->RChild!=NULL){
InLQueue(Q,p->RChild);
}
}
}
//ABD^G^^^CE^H^^F^^
int main(){
BiTree root;
BiTree *_root=&root;
printf("输入扩展先序序列\n");
//ABD^G^^^CE^H^^F^^
CreateBiTree(_root);
printf("先序序列(非递归)\n");
PreOrderN(root);//ABDGCEHF
printf("\n");
printf("中序序列-1(非递归)\n");
InOrderN1(root);//DGBAEHCF
printf("\n");
printf("中序序列-2(非递归)\n");
InOrderN2(root);//DGBAEHCF
printf("\n");
printf("后序序列(非递归)\n");
PostOrderN(root);//GDBHEFCA
printf("\n");
printf("层次遍历\n");
LevelOrder(root);//ABCDEFGH
printf("\n");
}
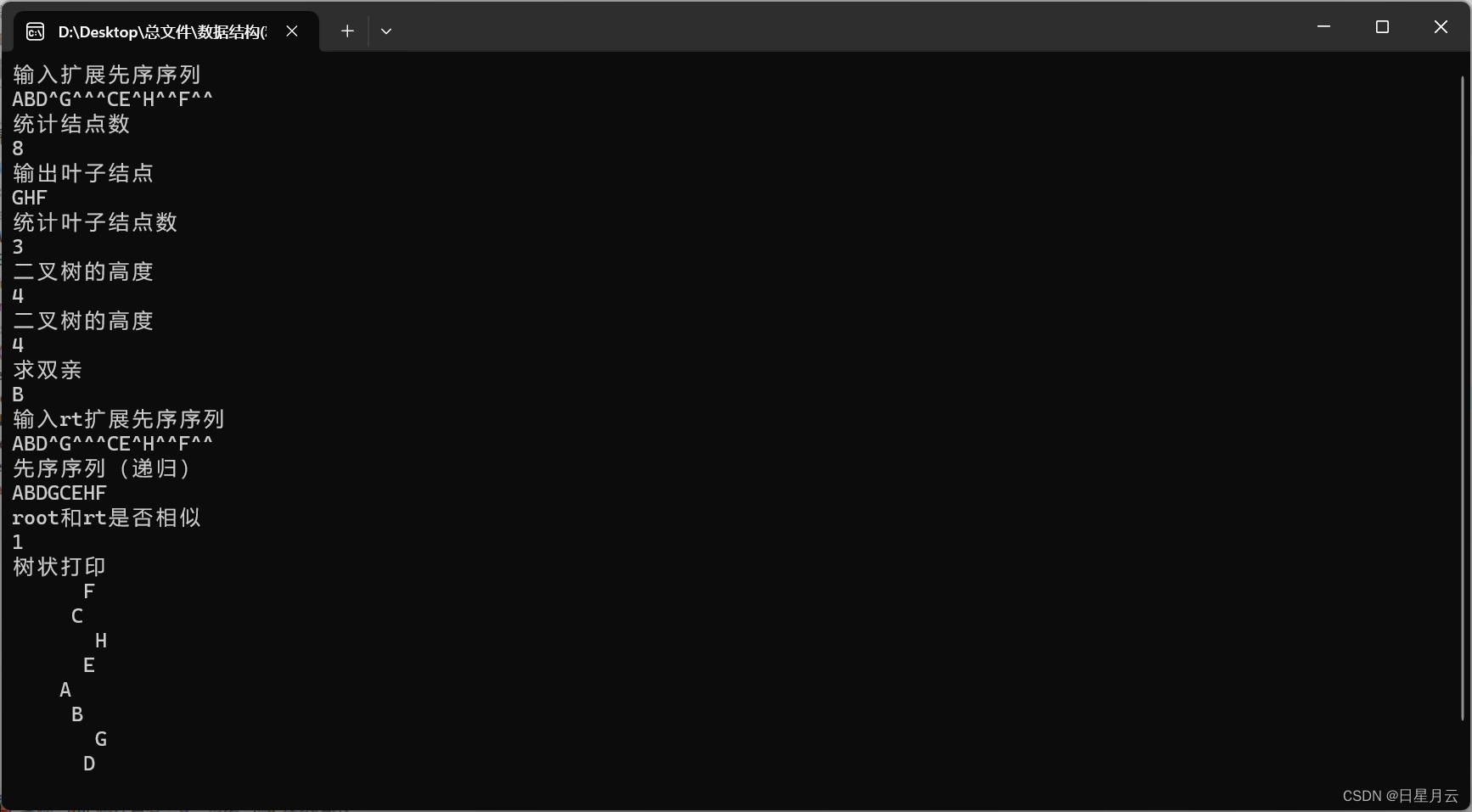
6.4.3 遍历算法的应用
1.统计二叉树的结点数
2.输出二叉树的叶子结点
3.统计二叉树的叶子结点数目
4.求二叉树的高度
5.求结点的双亲
6.二叉树相似性判定
7.按树状打印二叉树
8.创建二叉链表存储的二叉树
3-二叉树的遍历算法应用.c
#include<stdio.h>
#include<stdlib.h>
typedef char DataType;
typedef struct Node{
DataType data;
struct Node * LChild;
struct Node * RChild;
}BiTNode,*BiTree;
//【算法6-17】用扩展先序遍历序列创建二叉链表
void CreateBiTree( BiTree *root){
char ch;
ch=getchar();
if(ch=='^') * root= NULL;
else{
* root = (BiTree) malloc(sizeof(BiTNode));
(*root)->data=ch;
CreateBiTree(&((*root)->LChild));
/*以左子树域地址为参数,可使被调用函数中建立的结点指针置于该域中*/
CreateBiTree(&((*root)->RChild));
/*以右子树域地址为参数,可使被调用函数中建立的结点指针置于该域中*/
}
}
//访问
void Visit(DataType n){
printf("%c",n);
}
//【算法6-1】递归 先序
void PreOrder(BiTree root){
//先序遍历二叉树,root为根节点的指针
if(root){
Visit(root->data);
PreOrder(root->LChild);
PreOrder(root->RChild);
}
}
// 【算法6-9】先序遍历统计二叉树的结点数
int Count=0;
void CountWithPreOrder(BiTree root){
//Count为统计结点数目的全局变量,调用前初始值为0
if(root){
Count++;//统计结点数
CountWithPreOrder(root->LChild);//先序遍历左子树
CountWithPreOrder(root->RChild);//先序遍历右子树
}
}
// 【算法6-10】中序遍历输出二叉树的叶子结点
void PrintTNWithInOrder(BiTree root){
if(root){
PrintTNWithInOrder(root->LChild);
if(root->LChild==NULL&&root->RChild==NULL){
Visit(root->data);
}
PrintTNWithInOrder(root->RChild);
}
}
// 【算法6-11】后序遍历输出二叉树的叶子结点数目
int leaf(BiTree root){
int nl,nr;
if(root==NULL){
return 0;
}
if((root->LChild==NULL)&&(root->RChild==NULL)){
return 1;
}
nl=leaf(root->LChild);//递归求左子树的叶子数
nr=leaf(root->RChild);//递归求右子树的叶子数
return(nl+nr);
}
//【算法6-12】全局变量法求二叉树的高度
int depth=0;
void TreeDepth(BiTree root,int h){
//h为root结点所在的层次,首次调用前初始值为1
//depth为记录当前求得的最大层次的全局变量,调用前初始值为0
if(root){
if(h>depth) {
depth=h;//当前结点层大于depth,则更新
}
TreeDepth(root->LChild,h+1);//遍历左子树,子树根层次为h+1
TreeDepth(root->RChild,h+1);//遍历右子树,子树根层次为h+1
}
}
//【算法6-13】求二叉树的高度
int PostTreeDepth(BiTree root){
int hl,hr,h;
if(root== NULL) return 0;
else{
hl = PostTreeDepth(root->LChild);//递归求左子树的高度
hr= PostTreeDepth (root->RChild);//递归求右子树的高度
h=(hl>hr? hl:hr)+1; //计算树的高度
return h;
}
}
//【算法6-14】求二叉树中某一结点的双亲
BiTree parent( BiTree root, BiTree current){
//在以root为根的二叉树中找结点current的双亲
BiTree p;
if(root == NULL) return NULL;
if(root->LChild== current||root->RChild ==current)
return root; //root即为current的双亲
p=parent(root->LChild,current);//递归在左子树中找
if (p!=NULL) return p;
else return(parent (root->RChild,current));//递归在右子树中找
}
//【算法6-15】二叉树相似性判定
int like(BiTree t1, BiTree t2){
int like1, like2;
if(t1==NULL && t2==NULL) return 1;//t1,t2均空,则相似
if(t1==NULL||t2==NULL)return 0;//t1、t2仅一棵空,则不相似
like1=like(t1->LChild,t2->LChild);//递归判左子树是否相似
like2=like(t1->RChild,t2->RChild);//递归判右子树是否相似
return (like1 && like2);
}
//【算法6-16】按树状打印二叉树
void PrintTree( BiTree root, int h){
if(root == NULL) return;
PrintTree(root->RChild, h+1); //先打印右子树
int i;
for(i=0;i<h;i++) printf(" ");//层次决定结点的左右位置
printf("%c\n",root->data);//输出结点
PrintTree(root->LChild,h+1); //后打印左子树
}
//ABD^G^^^CE^H^^F^^
int main(){
BiTree root;
BiTree *_root=&root;
printf("输入扩展先序序列\n");
//ABD^G^^^CE^H^^F^^
CreateBiTree(_root);
if(Count!=0){
Count=0;
}
printf("统计结点数\n");
CountWithPreOrder(root);
printf("%d",Count);
printf("\n");
printf("输出叶子结点\n");
PrintTNWithInOrder(root);
printf("\n");
printf("统计叶子结点数\n");
int leafCount=leaf(root);
printf("%d",leafCount);
printf("\n");
if(depth!=0){
depth=0;
}
printf("二叉树的高度\n");
TreeDepth(root,1);
printf("%d",depth);
printf("\n");
printf("二叉树的高度\n");
int dpth=PostTreeDepth(root);
printf("%d",dpth);
printf("\n");
printf("求双亲\n");
BiTree current=(root->LChild)->LChild;
BiTree pt=parent(root,current);
Visit(pt->data);
printf("\n");
BiTree rt;
BiTree *_rt=&rt;
printf("输入rt扩展先序序列\n");
//ABD^G^^^CE^H^^F^^
fflush(stdin); //清一下输入的\n
CreateBiTree(_rt);
printf("先序序列(递归)\n");
PreOrder(rt);
printf("\n");
printf("root和rt是否相似\n");
int lk=like(root,rt);
printf("%d",lk);
printf("\n");
printf("树状打印\n");
int depth=PostTreeDepth(root);
PrintTree(root,depth);
}
6.4.4由遍历序列确定二叉树
1.由先序和中序确定二叉树
思想:
先序确定根结点
中序确定左右结点
2.由中序和后序确定二叉树
思想:
后序确定根结点
中序确定左右结点
6.5线索二叉树
6.5.1 线索二叉树的基本概念
在线索二叉树中,为了正确区分指向左右孩子的指针和指向前驱后驱的指针,将结点结构改为5个域,原二又链表中的左孩子域、数据域和右孩子域依战保持不变,增加左标志域Ltag和右标志域它们是两个布尔型的数据城。
线索二叉树的结点结构如下 :
LChild Ltag Data Rtarg RChild
①若结点有左子树,则LChild城仍指向其左孩子;否则,LChild域指向其遍历序列中的直接前驱结点
②若结点有右子树,则RChild域仍指向其右孩子;否则,RChild域指向其遍历序列中的直接后继结点
③ Lag和Rtag的定义如下:
{ 0 LChild域指示结点的左孩子
Ltag = {
{ 1 LChild域指示结点的遍历前驱
{ 0 RChild域指示结点的右孩子
Rtag = {
{ 1 RChid域指示结点的遍历后继
在上述存储结构中,指向前驱和后继结点的指针称为“线索”,对二叉树以某种次序进行遍历并且将空指针改为线索的过程叫做“线索化”,经过线索化的一叉树称为“线索二叉树”;以上述结点结构存储的含有线索的二叉链表称为“线索链表”
依据二叉树遍历策略的不同,存在三种不同的线索二叉树。依据二叉树的先序、中序、后序 遍历策略,分别对应有先序线索二叉树、中序线索二叉树和后序线索二叉树。
6.5.2 二叉树的线索化
略
6.5.3 线索二叉树的遍历
略
6.6 树和森林
6.6.1 树的存储
1.双亲表示法
双亲表示法的存储结构定义如下。
define MAX 100
typedef struct TNode{ /*顺序表结点结构定义。/
DataType data;
int parent;
}TNode;
typedef struct{ /*树的定义*/
TNode tree[MAX];
int root; /*树的根结点在表中的位置*/
int num; /*树的结点个数*/
}PTree;
2.孩子表示法
孩子表示法的存储结构定义如下。
typedef struct ChildNode{ //孩子链表结点结构定义
int Child;
Struct ChildNode * next;
}ChildNode;
typedef struct{ //顺序表结点结构定义
DataType data;
ChildNode w FirstChild;
| DataNode;
typedef struct{ //树的定义
DataNode nodes[ MAX];
int root; //树的根结点在顺序表中的位置
int num; //树的结点个数
| CTree;
3.孩子兄弟表示法
孩子兄弟表示法的存储结构定义如下。
typedef struet CSNode{
DataType data; /*结点信息*/
Struct CSNode * FirstChild; /*第一个孩子指针*/
Struct CSNode * NextSibling; /*右兄弟指针*/
}CSNode.* CSTree;
6.6.2 树、森林与二叉树的转换
略
6.6.3 树和森林的遍历
| 二叉树 | 树 | 森林 |
|---|---|---|
| 先序 | 先根 | 先序 |
| 中序 | 后根 | 中序 |
| 中序 | \ | 中序 |
6.7哈夫曼树及其应用
哈夫曼(Hufman)树,又称最优二叉树,是带权路径长度最短的树,来构造最优编码,用于信息传输、数据压缩等方面,是一种应用广泛的二叉树。
6.7.1哈夫曼树
在介绍哈夫量树之前,先介绍几个与哈夫曼树相关的基本概念
路径;树中个结点到另一个结点之间的分支序列构成两个结点间的路径,
路径长度:路径上分支的条数称为“路径长度”。
树的路径长度:从树根到每个结点的路径长度之和称为“树的路径长度”。
6.3节介绍的完全二叉树,是结点数给定的情况下路径长度最短的二叉树。
带权路径长度:结点到树根间的路径长度与结点的权的乘积,称为该结点的“带机
结点的权:给树中结点赋予一个数值,该数值称为“结点的权”。
树的带权路径长度:树中所有叶子结点的带权路径长度之和,称为“树的带权路径长度",常记为WPL:
WPL = ∑nk=1 Wkx,Lk
其中,n为叶子数,Wk为第k个叶子的权值,Lk为第k个叶子到树根的路径长度。
最优二叉树:在叶子个数n以及各叶子的权值W,确定的条件下,树的带权路径长度W 最小的二叉树称为“最优二叉树”。
1.哈夫曼树的建立
略
2.哈夫曼算法的实现
6.7.2哈夫曼编译码
1.哈夫曼编码的概念
信息压缩达到最短的前缀编码
2.哈夫曼编码的算法实现
3.哈夫曼编码的译码
6.8 实例分析与实现
6.8.1表达式树
略
6.8.2树与等价类的划分
略
6.8.3回溯法与N皇后问题
略
6.9 算法总结
略
实验
哈夫曼编码的实现
习题
1.单项选择题
(1)树最适合用来表示的结构是B。
A.元素间的有序结构
B.元素间具有分支及层次关系的结构
C.元素间的无序结构
D.元素间无联系的结构
(2)设一棵二叉树的结点个数为18,则它的高度至少为B
A.4
B.5
C.6
D.18
(3)任意一棵二叉树的叶子结点在其先序、中序、后序序列中的相对位置C
A.肯定发生变化
B.有时发生变化
C.肯定不发生变化
D.无法确定
4)判断线索二叉树中某结点P有左孩子的条件是C
A. p!=NULL
B.p->lchild!=NULL
C.p->LTag=0
D.p->LTag=1
(5)二叉树在线索化后,仍不能有效求解的问题是C
A.先序线索二叉树中求后继
B.中序线索二叉树中求后继
C.中序线索二叉树中求前驱
D.后序线索二叉树中求后继
(6)设森林T中有4棵树,其结点个数分别为n、nz、ng、ng,那么当森林T转换成一棵二叉树后,则根结点 的右子树上有 D 个结点。
A.n1-1
B.n1
C.n1+n2+n3
D.n2+n3+n4
(7)由权值分别为925.7的4个叶子结点构造一棵哈夫曼树,则该树的带权路径长度WPL为C
A.23
B.37
C.44
D.46
(8)设T是一棵哈夫曼树,有8个叶结点,则树T的高度最高可以是C
A.4
B.6
C.8
D.10
3.完成题
3完成题
(1)已知一棵二叉树的后序序列为ABCDEFG,中序序列为ACBCEDF。试完成下列操作。
①画出该二叉树的树形图。
G(C(A,B),F(E(^,D),^))
②给出该二叉树的先序序列。
GCABFED
③画出该二叉树的顺序存储结构示意图。
0 1 2 3 4 5 6 ... 13 ...
G C F A B E D
(2)已知一棵树的双亲表示法如下所示,试完成下列操作。
①画出该树的树形图。
A----------------------------------
B----------------------------------
E----------------------------------
K--------------------------
F----------------------------------
C--------------------------
M--------------------------
C--------------------------
G--------------------------
N--------------------------
H--------------------------
O--------------------------
D--------------------------
I--------------------------
J--------------------------
②画出该树的孩子兄弟二叉链表存储结构示意图。
A
B ^
E C
K F G D
^ ^ C ^ N H I ^
^ M ^ ^ O ^ ^ J
^ ^ ^ ^
③画出对应二叉树的中序线索二叉树。
中序:KELMFBNGOHCIJDA
(3)假设某通信报文的字符集由A、B、C、D、E、F共6个字符组成,它们在报文中出现的次数分别为16、12、9、30、3、6。试构造一棵哈夫曼树,并完成如下操作。
(76)
30 (46)
(18) (28)
(9) 9 12 16
3 6
①计算哈夫曼树的带权路径长度。
177
②写出各叶子结点对应字符的哈夫曼编码。
A B C D E F
111 110 101 0 1000 1001
4.算法设计题
(1)编写算法,在以二叉链表存储的二叉树中,求度为2的结点的个数。
#include<stdio.h>
#include<stdlib.h>
typedef char DataType;
typedef struct Node{
DataType data;
struct Node * LChild;
struct Node * RChild;
}BiTNode,*BiTree;
int Node2(BiTree T){
if(!T){
return 0;
}else if(T->LChild&&T->RChild){
return Node2(T->LChild)+Node2(T->RChild)+1;
}else{
return Node2(T->LChild)+Node2(T->RChild);
}
}
int main(){
BiTNode e={'E'};
BiTNode f={'F'};
BiTNode d={'D',&e,&f};
BiTNode b={'B'};
BiTNode c={'C'};
BiTNode a={'A',&b,&c};
BiTNode root={'0',&a,&d};
int res=Node2(&root);
printf("%d",res);//3
}
(2)编写算法,在以二叉链表存储的二叉树中,交换二叉树各结点的左右子树。
#include<stdio.h>
#include<stdlib.h>
typedef char DataType;
typedef struct TreeNode{
DataType data;
struct TreeNode * left;
struct TreeNode * right;
}BiTNode,*BiTree;
struct TreeNode* invertTree(struct TreeNode *root){
struct TreeNode* temp=NULL;
if(root==NULL){
return NULL;
}
temp=root->left;
root->left=root->right;
root->right=temp;
invertTree(root->left);
invertTree(root->right);
return root;
}
//访问
void Visit(DataType n){
printf("%c",n);
}
//【算法6-1】递归 先序
void PreOrder(BiTree root){
//先序遍历二叉树,root为根节点的指针
if(root){
Visit(root->data);
PreOrder(root->left);
PreOrder(root->right);
}
}
int main(){
BiTNode e={'E'};
BiTNode f={'F'};
BiTNode d={'D',&e,&f};
BiTNode b={'B'};
BiTNode c={'C'};
BiTNode a={'A',&b,&c};
BiTNode root={'0',&a,&d};
//翻转前
PreOrder(&root);
printf("\n");
BiTree r=invertTree(&root);
//翻转后
PreOrder(r);
}
最后
2023-11-6 17:03:04
我们都有光明的未来
不必感谢我,也不必记得我
祝大家考研上岸
祝大家工作顺利
祝大家得偿所愿
祝大家如愿以偿
点赞收藏关注哦









![[Linux] GRUB引导 学习笔记(一)](https://img-blog.csdnimg.cn/img_convert/d98a230bc7537e8d21c0ea8930418f5b.png)