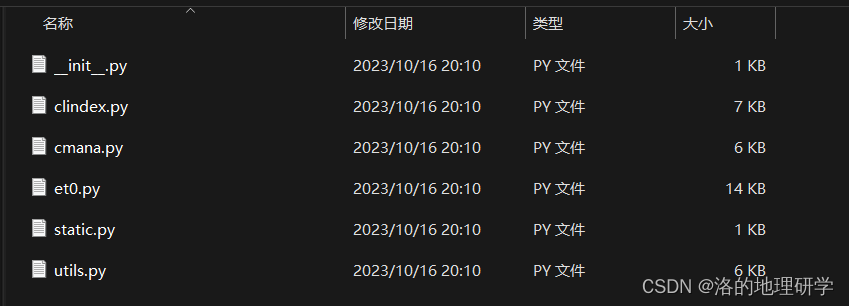
本模块的主要内建子模块如下：

如何获得完整代码： 回复博主 或者 留言/私信 。

注意：本代码完全开源，可随意修改使用。 但如果您的成果使用或参考了本段代码，给予一定的引用说明（非强制），包括但不限于：

• 1.作者：洛
• 2.网站：gma.luosgeo.com
• 3.PyPI：https://pypi.org/project/gma/
• 3.GitHub：https://github.com/LiChongrui

其中：

clindex：气候指标计算函数
cmana：气候诊断函数
et0：蒸散计算函数
static：气候常量
utils：通用工具

示例代:1：

from ..core.arraypro import *
from .utils import *

#################################### 累积概率计算
def GammaCP(Data, Axis):
    '''gamma 分布累积概率'''
    if np.nanmin(Data) < 0:
        Data = Data + np.abs(np.nanmin(Data)) * 2    
        # Data = Data + 1000

    PF = ParameterFitting(Data, Axis = Axis)
    Data = PF.Data
    Axis = PF.Axis

    # 计算 0 值概率并填充 0 值 为 NaN
    Zeros = (Data == 0).sum(axis = Axis, keepdims = True)
    ProbabilitiesOfZero = Zeros / Data.shape[Axis]
    Data[Data == 0] = np.nan

    Alphas, Betas = ParameterFitting(Data, Axis = Axis).MLE()
    # 使用gamma CDF 查找 gamma 概率值
    GammaProbabilities = stats.gamma.cdf(Data, a = Alphas, scale = Betas)
    
    Probabilities = ProbabilitiesOfZero + (1 - ProbabilitiesOfZero) * GammaProbabilities
    
    return Probabilities 

def LogLogisticCP(Data, Axis):
    '''Log-Logistic 分布累积概率'''
    PF = ParameterFitting(Data, Axis)
    Alpha, Beta, Gamma1 = PF.LMoment()
     
    Probabilities = 1 / (1 + (Alpha / (PF.Data - Gamma1)) ** Beta)
    
    # 由于 scipy 对 non 值处理过于简单，这里不使用 scipy 的函数
    # Probabilities = stats.fisk.cdf(PF.Data, Beta, loc = Gamma1, scale = Alpha)

    return Probabilities

def Pearson3CP(Data, Axis):
    '''pearson III 分布累积概率'''
    if np.nanmin(Data) < 0:
        Data = Data + np.abs(np.nanmin(Data)) * 2    

    PF = ParameterFitting(Data, Axis)
    Data = PF.Data
    Axis = PF.Axis  

    Loc, Scale, Skew = PF.LMoment2()

    Alpha = 4.0 / (Skew ** 2)
    MINPossible = Loc - ((Alpha * Scale * Skew) / 2.0)
    
    Zeros = (Data == 0).sum(axis = Axis, keepdims = True)
    ProbabilitiesOfZero = Zeros / Data.shape[Axis]

    Probabilities = stats.pearson3.cdf(Data, Skew, Loc, Scale)

    Probabilities[(Data < 0.0005) & (ProbabilitiesOfZero > 0.0)] = 0.0
    Probabilities[(Data < 0.0005) & (ProbabilitiesOfZero <= 0.0)] = 0.0005

    Probabilities[(Data <= MINPossible) & (Skew >= 0)] = 0.0005
    Probabilities[(Data >= MINPossible) & (Skew < 0)] = 0.9995

    Probabilities = ProbabilitiesOfZero + (1.0 - ProbabilitiesOfZero) * Probabilities

    return Probabilities

def _ReshapeAndExtend(Data, Axis, Periodicity):
    '''更改输入数据维度为 （Axis / Periodicity, Periodicity, N），并补充末尾缺失数据'''
    # 交换设置轴到 0 
    if Data.ndim > 1:
        Data = np.swapaxes(Data, 0, Axis)
        S = Data.shape
        S0, S1 = S[0], np.prod(S[1:], dtype = int)
        Data = Data.reshape((S0, S1))
    else:
        Data = np.expand_dims(Data, -1)
    
    # 填充不足 Data.shape[0] / Periodicity
    B = Data.shape[0] % Periodicity
    PW = 0 if B == 0 else Periodicity - B
    
    Data = np.pad(Data, ((0, PW), (0,0)), mode = "constant", constant_values = np.nan)
    
    # 更改为目标维度（3维）
    PeriodicityTimes = Data.shape[0] // Periodicity 
    
    return Data.reshape(PeriodicityTimes, Periodicity, Data.shape[1])

def _RestoreReshapeAndExtend(Data, Axis, Shape):
    '''对 _ReshapeAndExtend 修改的维度和数据进行还原'''
    # 还原为原始维度（2维）
    Data = Data.reshape(np.prod(Data.shape[:2]), *Data.shape[2:])

    # 去除尾部填充值
    Data = Data[:Shape[Axis]]

    # 还原到初始状态
    SHP = list(Shape)
    SHP.pop(Axis)
    SHP = [Shape[Axis]] + SHP

    Data = Data.reshape(SHP)
    Data = np.swapaxes(Data, Axis, 0)
    
    return Data

############### 不同的计算方式
def _Fit(WBInScale, Periodicity, Distribution):
    '''计算标准化指数'''
    # 1.计算累积概率
    Probabilities = eval(f'{Distribution}CP')(WBInScale, 0)
    if Periodicity == 1:
        Probabilities = np.expand_dims(Probabilities, 1)
        
    # 2.生成结果
    OutInScale = stats.norm.ppf(Probabilities)
    return OutInScale

def _API(WBInScale, Axis):
    '''计算距平指数'''
    # 1.计算平均值或趋势值
    Mean = np.nanmean(WBInScale, axis = Axis, dtype = np.float64, keepdims = True)
    
    # 4.生成结果
    OutInScale = (WBInScale - Mean) / Mean
    
    return OutInScale

############### 计算结果
def _Compute(Data, Axis, Scale, Periodicity, Distribution):
    '''自动计算'''   
    Periodicity = ValueType(Periodicity, 'pint')
    
    # 0.数据准备
    DP = DataPreparation(Data, Axis) 
    Data = DP.Data
    SHP = Data.shape
    Axis = DP.Axis
    
    # 1.计算尺度
    WBInScale = DP.SumScale(Scale)
    if not (SHP[Axis] > Periodicity) and (SHP[Axis] > Scale):
        return np.full(WBInScale.shape, np.nan)

    # 2.更改输入数据维度为 （Axis / Periodicity, Periodicity, N）
    WBInScale = _ReshapeAndExtend(WBInScale, Axis, Periodicity)

    # 3.生成结果
    if Distribution == 'API':
        OutInScale = _API(WBInScale, Axis)
    else:
        OutInScale = _Fit(WBInScale, Periodicity, Distribution)

    # 4.还原数据
    OutInScale = _RestoreReshapeAndExtend(OutInScale, Axis, SHP)    
    
    return OutInScale

示例代码2：

#################################### SPEI
def SPEI(PRE, PET, Axis = None, Scale = 1, Periodicity = 12, Distribution = 'LogLogistic'):
    '''计算SPEI'''
    Distribution = GetDistribution(Distribution)
    PRE, PET = INITArray(PRE, PET)

    WB = np.subtract(PRE, PET, dtype = PRE.dtype)
    
    SPEIInScale = _Compute(WB, Axis, Scale, Periodicity, Distribution)
    
    return SPEIInScale

#################################### SPI
def SPI(PRE, Axis = None, Scale = 1, Periodicity = 12, Distribution = 'Gamma'):
    '''计算 SPI'''
    Distribution = GetDistribution(Distribution)
    SPIInScale = _Compute(PRE, Axis, Scale, Periodicity, Distribution)
    
    return SPIInScale

#################################### PAP
def PAP(PRE, Axis = None, Scale = 1, Periodicity = 12):
    '''降水距平百分率'''
    PAPInScale = _Compute(PRE, Axis, Scale, Periodicity, 'API') 
    
    return PAPInScale