目录
1 遗传选择
2 遗传交叉
3 遗传变异
4 结语
1 遗传选择
我们书接上回,我们完成了种群的初始化,将所有的种群放入了new_pop1中,这个new_pop1是一个(种群大小 * 路径)的一个矩阵,我们来看如何进行遗传选择:
% 循环迭代操作 for i = 1 : max_gen % 计算适应度值 % 计算路径长度 path_value = cal_path_value(new_pop1, x) % 计算顺滑度 path_smooth = cal_path_smooth(new_pop1, x) % 计算适应度 fit_value = 1 .* path_value .^ -1 + 1 .* path_smooth .^ -1; % 这行代码计算了路径长度的均值,并将其赋值给名为 mean_path_value 的数组的第 i 个元素。 mean_path_value(1, i) = mean(path_value); % 这行代码找到了适应度值中的最大值,并将其索引赋值给 m。 [~, m] = max(fit_value); % 这行代码将在适应度值中找到的最大值对应的路径长度赋值给 min_path_value 数组的第 i 个元素。 min_path_value(1, i) = path_value(1, m); % 选择操作 new_pop2 = selection(new_pop1, fit_value); % 交叉 new_pop2 = crossover(new_pop2, pc); % 变异 new_pop2 = mutation(new_pop2, pm, G, x); % new_pop1 = new_pop2; end我们这里迭代50次,也就是说50代,我们进行50代的进化。我们首先计算路径长度:
% 计算路径长度函数 传进来的是个体 function [path_value] = cal_path_value(pop, x) [n, ~] = size(pop); path_value = zeros(1, n); for i = 1 : n single_pop = pop{i, 1}; [~, m] = size(single_pop); for j = 1 : m - 1 % 点i所在列 (从左到右编号1.2.3...) x_now = mod(single_pop(1, j), x) + 1; % 点i所在行(从上到下编号1,2,3...) y_now = fix(single_pop(1, j) / x) + 1; % 点i+1所在行、列 x_next = mod(single_pop(1, j + 1), x) + 1; y_next = fix(single_pop(1, j + 1) / x) + 1; % 左右上下相连 if abs(x_now - x_next) + abs(y_now - y_next) == 1 path_value(1, i) = path_value(1, i) + 1; else path_value(1, i) = path_value(1, i) + sqrt(2); end end end我们传进来的是所有的个体,在循环中遍历每一个个体for i = 1 : n,pop{i, 1} 表示从 pop 中提取第 i 行、第 1 列的元素。我们将绝对栅格坐标值转化为栅格坐标求两坐标的距离,如果相连则路径+1如果是斜对角则路径+根号2。最后我们得到了一个(1,n)的数组,保存了每一个路径的代价值。
我们在来看计算顺滑度:
% 计算顺滑度 function [path_smooth] = cal_path_smooth(pop, x) [n, ~] = size(pop); path_smooth = zeros(1, n); % 遍历所有个体 for i = 1 : n single_pop = pop{i, 1}; [~, m] = size(single_pop); % 遍历一个个体的所有点 for j = 1 : m - 2 % 计算三个点的坐标 列 行 i i+1 i+2 x_now = mod(single_pop(1, j), x) + 1; y_now = fix(single_pop(1, j) / x) + 1; x_next1 = mod(single_pop(1, j + 1), x) + 1; y_next1 = fix(single_pop(1, j + 1) / x) + 1; x_next2 = mod(single_pop(1, j + 2), x) + 1; y_next2 = fix(single_pop(1, j + 2) / x) + 1; % cos A=(b?+c?-a?)/2bc b2 = (x_now - x_next1)^2 + (y_now - y_next1)^2; c2 = (x_next2 - x_next1)^2 + (y_next2 - y_next1)^2; a2 = (x_now - x_next2)^2 + (y_now - y_next2)^2; cosa = (c2 + b2 - a2) / (2 * sqrt(b2) * sqrt(c2)); % 度数 angle = acosd(cosa); if angle < 170 && angle > 91 path_smooth(1, i) = path_smooth(1, i) + 3; elseif angle <= 91 && angle > 46 path_smooth(1, i) = path_smooth(1, i) + 15; elseif angle <= 46 path_smooth(1, i) = path_smooth(1, i) + 20; end end end
我们遍历每一个个体,计算三个点的夹角,越平滑的话角度越大,我们给予角度大的较小权值。
我们计算适应度:
综上所述,越好的路径适应度越大,适应环境也就越强。
下面计算了路径长度的均值,并将其赋值给名为 mean_path_value 的数组的第 i 个元素。又找到了适应度值中的最大值,并将其索引赋值给 m。又将在适应度值中找到的最大值对应的路径长度赋值给 min_path_value 数组的第 i 个元素。
% 计算适应度 fit_value = 1 .* path_value .^ -1 + 1 .* path_smooth .^ -1; % 这行代码计算了路径长度的均值,并将其赋值给名为 mean_path_value 的数组的第 i 个元素。 mean_path_value(1, i) = mean(path_value); % 这行代码找到了适应度值中的最大值,并将其索引赋值给 m。 [~, m] = max(fit_value); % 这行代码将在适应度值中找到的最大值对应的路径长度赋值给 min_path_value 数组的第 i 个元素。 min_path_value(1, i) = path_value(1, m);到此为止,我们的准备工作就完成了,我们进入选择工作:
% 选择操作 new_pop2 = selection(new_pop1, fit_value);我们看下选择操作的代码:
% 用轮盘赌法选择新的个体 % 输入变量 pop元素种群 fitvalue适应度值 % 输出变量 newpop选择以后的元素种群 function [new_pop] = selection(pop, fit_value) % 构造轮盘 % px存放有多少个个体 [px, ~] = size(pop); % 这行代码计算了适应度值的总和,将结果赋值给变量 total_fit。 total_fit = sum(fit_value); % 这行代码计算了每个个体的适应度相对于总适应度的比例,将结果存储在向量 p_fit_value 中。相当于一个大的转盘。每个部分占比多少 p_fit_value = fit_value / total_fit; % 这行代码对适应度比例进行累积求和,得到了一个逐步递增的概率分布。 0.2 0.5 0.8 1.0 p_fit_value = cumsum(p_fit_value); % 随机数从小到大排列 生成了若px=20 个0-1的列向量 ms = sort(rand(px, 1)); fitin = 1; newin = 1; % 举个例子 px = 4 ms = 0.1 0.2 0.3 0.4 p_fit_value = 0.3 0.6 0.65 0.75 % 好像没有做选择呢?? % D1 1<=4 ms(1)=0.1<p_fit_value(1)0.3 new_pop[1,1]=pop[1,1] newin=2 % D2 2<=4 ms(2)=0.2<p_fit_value(1)0.3 new_pop[2,1]=pop[1,1] newin=3 % D3 3<=4 ms(3)=0.3!=p_fit_value(1)0.3 fit_in = 2 % D4 3<=4 ms(3)=0.3<=p_fit_value(2)0.6 new_pop[3,1]=pop[2,1] newin=4 % D5 4<=4 ms(4)=0.4<=p_fit_value(2)0.6 new_pop[4,1]=pop[2,1] newin=4 while newin <= px if(ms(newin)) < p_fit_value(fitin) % 判断哪一次落在哪个区间里面 new_pop{newin, 1} = pop{fitin, 1}; newin = newin+1; else fitin = fitin+1; end end输入变量:pop种群,fitvalue为种群的每个个体适应度值的列表。上面我也用具体例子解释了,选择类似轮盘赌的方式,到这为止,我们从种群出选择出了new_pop作为自然选择的结果,其他种群全部抛弃。
2 遗传交叉
function [new_pop] = crossover(pop, pc) [px,~] = size(pop); % 判断路经点是奇数倍还是偶数倍 如果是奇数的话那么最后我们就不做处理了 parity = mod(px, 2); new_pop = {}; % 这是一个循环,它会以步长为2从1开始遍历到 px-1,目的是处理两两配对的个体。 for i = 1:2:px-1 singal_now_pop = pop{i, 1}; singal_next_pop = pop{i+1, 1}; % 这行代码使用 ismember 函数找出 singal_now_pop 中与 singal_next_pop 相同的元素,并返回一个逻辑数组 lia 和对应的索引 lib。 [lia, lib] = ismember(singal_now_pop, singal_next_pop); % 这行代码找出逻辑数组 lia 中为 1 的元素的索引,将结果存储在向量 n 中。 [~, n] = find(lia == 1); % 这行代码获取向量 n 的长度(即匹配的元素个数),并将结果存储在变量 m 中。 [~, m] = size(n); % 这是一个条件判断,它首先检查随机数是否小于交叉概率 pc,然后再检查匹配的元素个数是否大于等于3 if (rand < pc) && (m >= 3) % 如果上述条件成立,这行代码会生成一个介于2和m-1之间的随机整数 r。 r = round(rand(1,1)*(m-3)) +2; % 这两行代码分别得到要进行交叉的位置索引 crossover_index1 = n(1, r); crossover_index2 = lib(crossover_index1); % 这两行代码进行了交叉操作,生成了新的个体。 new_pop{i, 1} = [singal_now_pop(1:crossover_index1), singal_next_pop(crossover_index2+1:end)]; new_pop{i+1, 1} = [singal_next_pop(1:crossover_index2), singal_now_pop(crossover_index1+1:end)]; else % 如果交叉条件不满足,保持原个体不变。 new_pop{i, 1} =singal_now_pop; new_pop{i+1, 1} = singal_next_pop; end % 如果个体数量为奇数,将最后一个个体直接放入新一代。 if parity == 1 new_pop{px, 1} = pop{px, 1}; end end我们调用的函数是:
new_pop2 = crossover(new_pop2, pc);这里的pc = 0.8代表的是交叉处理频率,也就是我们有80%的几率进行交叉操作,内部是一个循环,它会以步长为2从1开始遍历到种群数量-1,目的是处理两两配对处理基因重组的个体。
我们先取出第一个种群和第二个种群,使用 ismember 函数找出 singal_now_pop 中与 singal_next_pop 相同的元素,并返回一个逻辑数组 lia 和对应的索引 lib。找出逻辑数组 lia 中为 1 的元素的索引,将结果存储在向量 n 中。获取向量 n 的长度(即匹配的元素个数),并将结果存储在变量 m 中。
如果路径的共同元素数量大于3且要进行遗传交叉操作我们将随机选取第一个种群的基因打乱拼接到第二个种群上,图示如下:
到这为止,我们已经对两两种群进行了基因重组。
3 遗传变异
% 变异频率 栅格地图 20 function [new_pop] = mutation(pop, pm, G, x) % 获取路径长度 [px, ~] = size(pop); new_pop = {}; % 它将会迭代处理种群中的每一个个体 for i = 1:px % 初始化最大迭代次数 max_iteration = 0; % 从种群 pop 中取出第 i 个个体,并将其赋值给变量 single_new_pop。 single_new_pop = pop{i, 1}; % 这行代码获取了 single_new_pop 的维度信息,并将列数保存在变量 m 中。 [~, m] = size(single_new_pop); % single_new_pop_slice初始化 single_new_pop_slice = []; % 这是一个条件语句,它检查一个随机数是否小于变异率 pm。 if(rand < pm) while isempty(single_new_pop_slice) % 生成两个随机整数 mpoint,这两个整数位于 2 到 m-2 之间。 mpoint = sort(round(rand(1,2)*(m-3)) + [2 2]); % 从 single_new_pop 中取出索引为 mpoint(1,1)-1 和 mpoint(1,2)+1 的两个元素,构成 single_new_pop_slice。 single_new_pop_slice = [single_new_pop(mpoint(1, 1)-1) single_new_pop(mpoint(1, 2)+1)]; % 使路径连续 single_new_pop_slice = generate_continuous_path(single_new_pop_slice, G, x); if max_iteration >= 100000 break end end % 不变异了 if max_iteration >= 100000 new_pop{i, 1} = pop{i, 1}; % 如果未达到最大迭代次数,将变异后的个体重新组合,并保存到 new_pop 中。 else new_pop{i, 1} = [single_new_pop(1, 1:mpoint(1, 1)-1), single_new_pop_slice(2:end-1), single_new_pop(1, mpoint(1, 2)+1:m)]; end % 将 single_new_pop_slice 重置为空,准备进行下一次循环。 single_new_pop_slice = []; else % 直接将未发生变异的个体复制到 new_pop 中。 new_pop{i, 1} = pop{i, 1}; end end这里的调用函数如下:
new_pop2 = mutation(new_pop2, pm, G, x);是我们在交叉里面得到的种群,pm是变异比率,我们设置为0.2。这里是对种群中的每一个个体进行变异的,对其随机两个点进行拼接,若拼接成功则变异成功。
4 结语
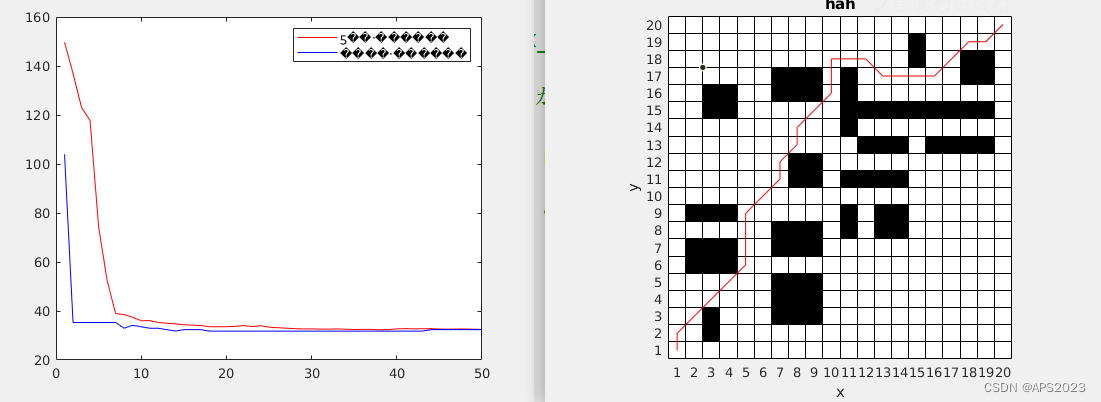
最后我们不断迭代出了最优路径:
接下来的代码段是用来将最优路径的节点坐标转换成具体的坐标值。它通过取模和整除操作来计算 x 和 y 的坐标值。
最后一段代码用红色绘制了最优路径在图形上。
min_path_value(1, end) [~, min_index] = max(fit_value); min_path = new_pop1{min_index, 1}; figure(2) hold on; title('hah'); xlabel('x'); ylabel('y'); DrawMap(G); [~, min_path_num] = size(min_path); for i = 1:min_path_num x_min_path(1, i) = mod(min_path(1, i), x) + 1; y_min_path(1, i) = fix(min_path(1, i) / x) + 1; end hold on; plot(x_min_path, y_min_path, 'r')最后看一下效果吧~