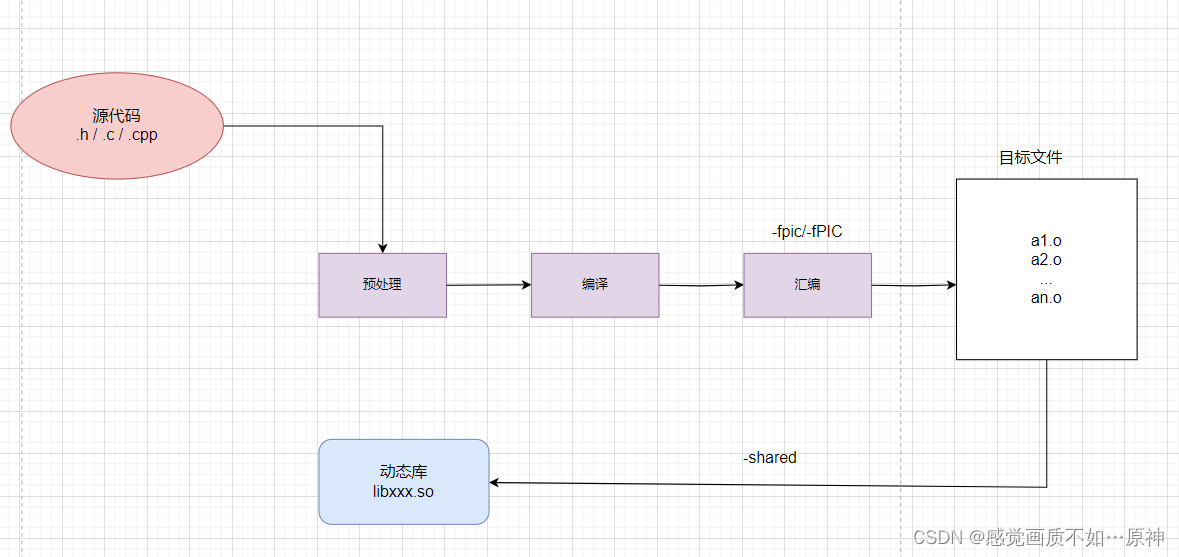
给了我们n阶楼梯让我们去爬，每次只能爬1阶或2阶，这个我们可以使用递归的方法进行解决，向上爬的过程与向下降的过程是一样的，所以我们就可以这样考虑，现在就是n阶楼梯每一次下降1阶或2阶有多少种方法刚好下降到0阶。

int climbStairs(int n){
    if(n==0){
        return 1;
    }else if(n<0){
        return 0;
    }
    return climbStairs(n-1)+climbStairs(n-2);
}

运行结果截图：

接下来我们就使用栈这种数据结构来进行问题的解决，思路还是一样的；这是一段可行的代码，但是因为在元素出栈时花费了大量的时间所以时间效率上比递归要慢，但是这是可以进行优化的，我们可以比如增加一个最近的1的标志flag用来记录最近的依次登阶为1的下标，然后设置一个数组记录每一次登阶之后所在的高度，这样就可以省去while循环的过程，直接找到对应的位置，这种优化就由读者自行优化。
当然如果你有其他的办法的话，请你在评论区评论，期待你的发言。

int climbStairs(int n){
    int *stack = (int *)malloc(sizeof(int)*(n+1));
    int num = 0;
    int * p;
    int m = n;
    while(n>0){
    	for(int i=0;i<m;i++){
    		stack[i] = 1;
    		n--;
		}
	}
	p = &stack[m-1];
    while(1){
    	if(n>0){
    		n-=1;
    		*(++p) = 1;
		}else{
			if(n == 0){
				num++;
			}
			while(*p==2&&p!=stack){
				*p = 0;
				p--;
				n+=2;
			}
			if(stack[0]==2&&p==stack){
				break;
			}
			*p = 2;
			n -= 1;
		}
    }
    return num;
}