LeetCode 面试题 16.17. 连续数列

news2024/11/27 12:35:03

文章目录

一、题目
二、C# 题解

一、题目

给定一个整数数组，找出总和最大的连续数列，并返回总和。

示例：

输入： [-2,1,-3,4,-1,2,1,-5,4]
输出： 6
解释： 连续子数组 [4,-1,2,1] 的和最大，为 6。

进阶：

如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的分治法求解。

点击此处跳转题目。

二、C# 题解

使用动态规划可以实现 O(n) 的复杂度。使用 max 记录以 j 结尾的最大连续和，其递推关系为：

$MAX\left\{ \begin{array}{l l} max[j-1]+nums[j],&nums[j]>0\\ max[j-1],&nums[j]\leq0\\ nums[j],&max[j-1]<0 \end{array} \right.$

每次纳入 nums[j] 并考虑：

max < 0，则直接从 j 开始就好，即设置 max = 0。因为算上前面的序列，和只会更小。
max += nums[j]，与 ans 比较，ans 结果取最大值。

理论上需要开辟一个 O(n) 数组存储 max，但是由于只需要求 max 的最大值 ans，因此可以边计算边更新 ans，省去了 O(n) 的空间。

public class Solution {
	public int MaxSubArray(int[] nums) {
        int ans = nums[0], max = ans;

        for (var j = 1; j < nums.Length; j++) {
            if (max < 0) max = 0;     // 先前的序列如果 < 0，则直接抛弃，从第 j 位开始重新计数
            max += nums[j];           // 并入第 j 位
            if (max > ans) ans = max; // 更新结果
        }

        return ans;
    }
}

时间：84 ms，击败 61.11% 使用 C# 的用户
内存：38.23 MB，击败 77.78% 使用 C# 的用户

使用分治可以实现 O(logn) 的复杂度。将数组 nums 一分为二，记为 left 和 right。则 nums 的答案 Max 可能有如下 3 中情况：

在 left 中。
在 right 中。
在 left 和 right 交界处。

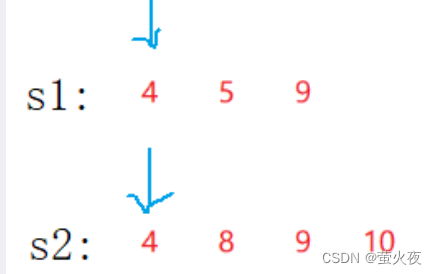
因此，需要记录区间的左端最大连续和 LMax（红色）与右端最大连续和 RMax（黄色），其对应的更新情况如下：

LMax：
RMax：

同时，使用 Sum（绿色）记录区间的总长度。

public class Solution {
    public struct Range
    {
        public int LMax; // 从左端开始的最长连续和
        public int RMax; // 以右端结尾的最长连续和
        public int Sum;  // 区间总和
        public int Max;  // 区间内最长连续和

        public Range(int l, int r, int s, int m) {
            LMax = l;
            RMax = r;
            Sum = s;
            Max = m;
        }

        public static Range operator +(Range left, Range right) {
            int lMax = Math.Max(left.LMax, left.Sum + right.LMax);
            int rMax = Math.Max(right.RMax, left.RMax + right.Sum);
            int sum  = left.Sum + right.Sum;
            int max  = Math.Max(Math.Max(left.Max, right.Max), left.RMax + right.LMax);
            return new Range(lMax, rMax, sum, max);
        }
    }

    public int MaxSubArray(int[] nums) {
        return Partition(nums, 0, nums.Length - 1).Max;
    }

    public Range Partition(int[] nums, int i, int j) {
        if (i == j) return new Range(nums[i], nums[i], nums[i], nums[i]);
        int mid = (i + j) >> 1;
        return Partition(nums, i, mid) + Partition(nums, mid + 1, j);
    }
}