题目

现有一个单位反馈系统的开环传递函数为

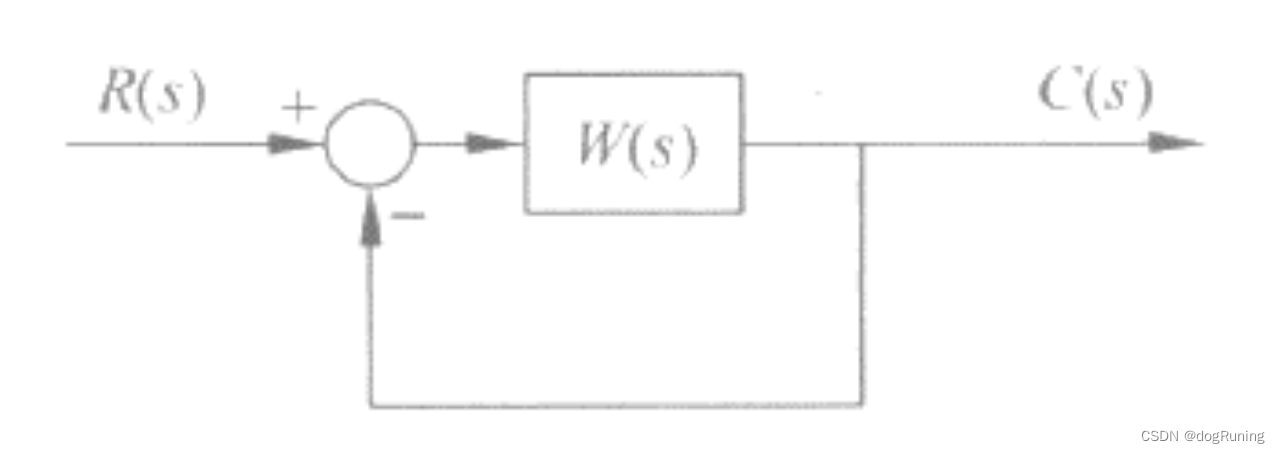
试对该系统进行以下分析。
1.基础分析
计算该系统的闭环传递函数。
2.稳定性分析
2.1 使用劳斯判据分析该系统的稳定性
2.2 使用MATLAB编程，计算该系统有关于稳定性分析的零、极点，分析其稳定性。
3.暂态性能分析
3.1 使用MATLAB编程，绘制该系统的单位脉冲响应、单位阶跃响应、单位斜坡响应、单位抛物线响应。
4.稳态性能分析
4.1 计算该系统的稳态位置误差系数、稳态速度误差系数、稳态加速度误差系数。
4.2 使用MATLAB编程，计算该系统面对三种输入信号时的给定稳态误差。
5.根轨迹分析
若将该系统开环传递函数的分子乘以，使用MATLAB编程，绘制该系统以为参数的根轨迹，并回答：在处于哪一范围时系统稳定。
6.频域分析
分析该系统伯德图的增益子图，至少需要说明该系统增益子图的估算图像共有几段、各段的斜率、以及各交接频率的取值。学有余力的同学可以直接画出该系统伯德图的精确图像。

/Users/doghuang/Desktop/Desktop/咸鱼/2023/仿真/咸鱼/电力电子_自学/电力电子和电力拖动控制系统的MATLAB仿真/第五章 电力电子变流电路的仿真/5_1 交流-直流变流器

untitled
闭环传递函数 T(s):
tf - 属性:

   Numerator: {[0 0 0 0 1 13]}
 Denominator: {[1 0 27.8000 202.6000 173 206]}
    Variable: 's'
     IODelay: 0
  InputDelay: 0
 OutputDelay: 0
   InputName: {''}
   InputUnit: {''}
  InputGroup: [1×1 struct]
  OutputName: {''}
  OutputUnit: {''}
 OutputGroup: [1×1 struct]
       Notes: [0×1 string]
    UserData: []
        Name: ''
          Ts: 0
    TimeUnit: 'seconds'
SamplingGrid: [1×1 struct]

系统可能是不稳定的（有特征值的实部为正或有零实部的特征值）。
系统的零点：
-13
系统的极点：
2.3691 + 6.3576i
2.3691 - 6.3576i
-3.9580 + 0.0000i
-0.3901 + 0.9892i
-0.3901 - 0.9892i
系统可能是不稳定的（有极点的实部为正或有零实部的极点）。
稳态位置误差系数 (Kp) = 0.9406
稳态速度误差系数 (Kv) = 15.8462
稳态加速度误差系数 (Ka) = 0.0000
稳态误差 (r(t) = 1): -547720.181638
稳态误差 (r(t) = t): -2465547.730435
稳态误差 (r(t) = 0.5*t^2): -241847.045931