1.消失的数字

面试题 17.04. 消失的数字 - 力扣（LeetCode）https://leetcode.cn/problems/missing-number-lcci/

这个题目当然有好几种解法，这里我推荐一种比较优秀的思路，也就是单身狗思路：异或。

异或的特点是相异为一，相同为0，也就是两个相同的数字异或就等于0.

那么我们只需要使用两个循环就能解决问题。

第一个循环遍历nums这个数组的所有元素，由于少了一个元素5，所以判断条件是i<numsSize,假设数组中的元素如下所示，那么第二个循环只需要将这个消失的数字补上，判断条件就是i<=numsSize,然后tail和i进行异或。

那么我们就可以理解为tail在同时遍历两个数组，这里大家需要知道的一个小知识是3^4^3^4的最终结果还是0，因为这里可以使用交换律，就是3^3^4^4,就相当与两个0最后异或，还是0。除了消失的数字出现一次，其他的数字都是成对出现，所以tail结果两次遍历异或后就是消失的那个数字。

int missingNumber(int* nums, int numsSize)
{
   int tail=0,i;
   for(i=0;i<numsSize;i++)
   {
       tail^=nums[i];
   }
   for(i=0;i<=numsSize;i++)
   {
       tail^=i;
   }
   return tail;
}

 2.轮转数组

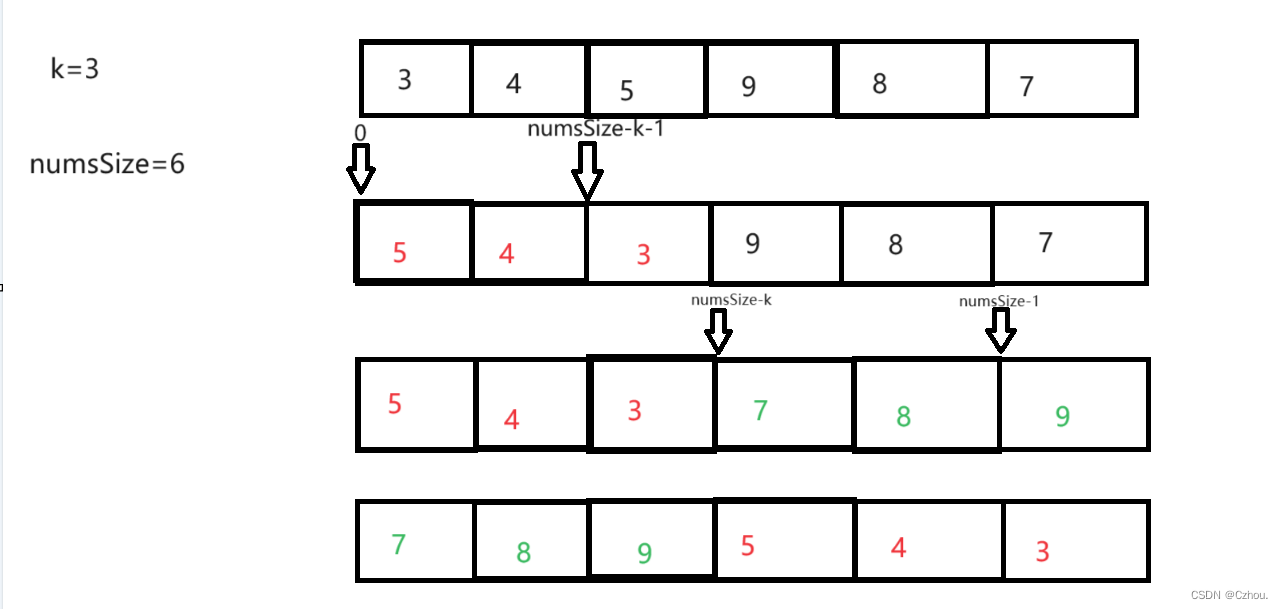
189. 轮转数组 - 力扣（LeetCode）https://leetcode.cn/problems/rotate-array/description/这里我也提供一种比较优的思路，我们需要将这个数组逆置3次，第一次逆置前numsSize-1-k个元素，因为numsSize是元素个数，逆置的位置是下标，所以需要-1，第二次逆置后k个，第三次就是整体逆置。这种方法非常难想到，但是效率很高。

void Func(int* nums,int left,int right)
{
    while(left<=right)
    {
        int tmp=nums[left];
        nums[left]=nums[right];
        nums[right]=tmp;
        left++;
        right--;
    }
}
void rotate(int* nums, int numsSize, int k)
{
   if(k>=numsSize)
   {
       k=k%numsSize;
   }
   //第一次逆置前numsSize-k个
   Func(nums,0,numsSize-k-1);
   //第二次逆置后k个
   Func(nums,numsSize-k,numsSize-1);
   //第三次将整个数组逆置
   Func(nums,0,numsSize-1);
}