[动态规划] (八) LeetCode 931.下降路径最小和

931. 下降路径最小和

题目解析

(1) n*n的整型数组

(2) 找出下降路径最小和

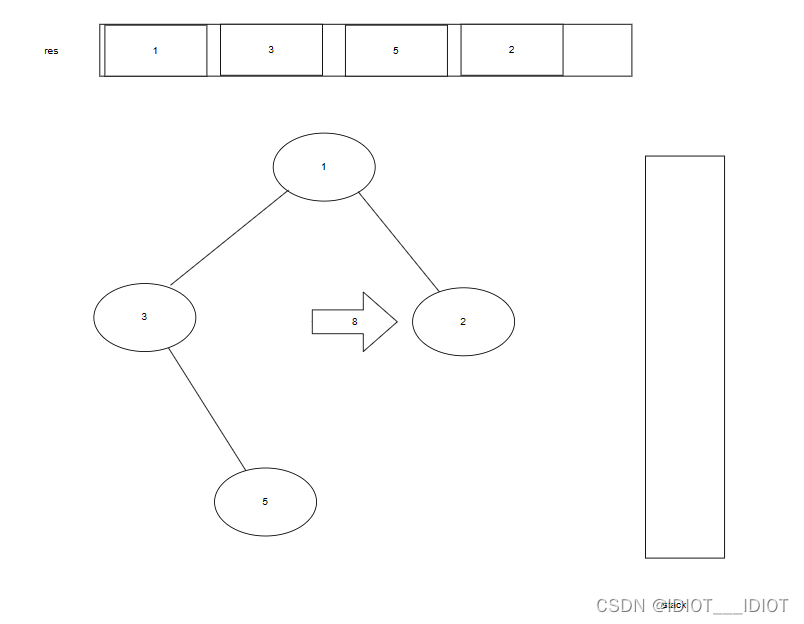
(3) 下降路径：可以从(i，j)到(i+1，j-1)、(i+1，j)、(i+1，j+1)三个任一位置。

如图：(1，1) => (2,，0)或(2，1)或(2，2)

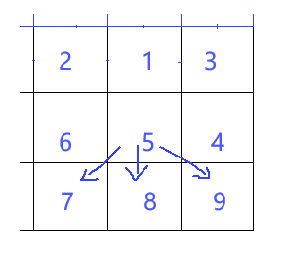
(4) 从第一行到最后一行就是一个完整的下降路径。

解题思路

状态表示

dp[i] [j]：按照以往的经验，以(i，j)为终点的最小和。

状态转移方程

dp[i] [j]取决于三个位置：dp[i-1] [j-1]、dp[i-1] [j]、dp[i-1] [j+1]位置的元素。

求最小和，就是找出它们三个的最小值+当前位置(i，j)的元素值。

所以

dp[i][j] = min(dp[i-1][j-1], min(dp[i-1][j], dp[i-1][j+1])) 
			+ (i,j)对应位置元素

初始化和填表顺序

• 初始化

由于需要访问i-1、j-1、j+1的位置，边界情况有：数组的最外层，如：

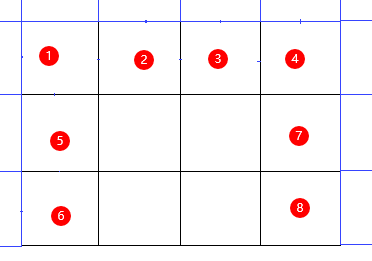
所以我们多开辟两列+一行即可。

在初始化时，由于5、6号位置或者7、8号位置等会出现访问多开辟出来的列的位置，这些多开辟出来的位置不能影响我们求最小和，所以多开辟的两列应该不被选中，即初始化为整数最大值。

而1、2、3、4等位置，为正常执行状态转移方程的逻辑，所以多开辟出的第一行应该初始化为0。

• 填表顺序

一列一列填表。

返回值

题目要求求最小和，所以返回dp数组中最后一行最小的元素。

看到这里就可以去尝试实现代码了，然后再继续看下面的内容。

---

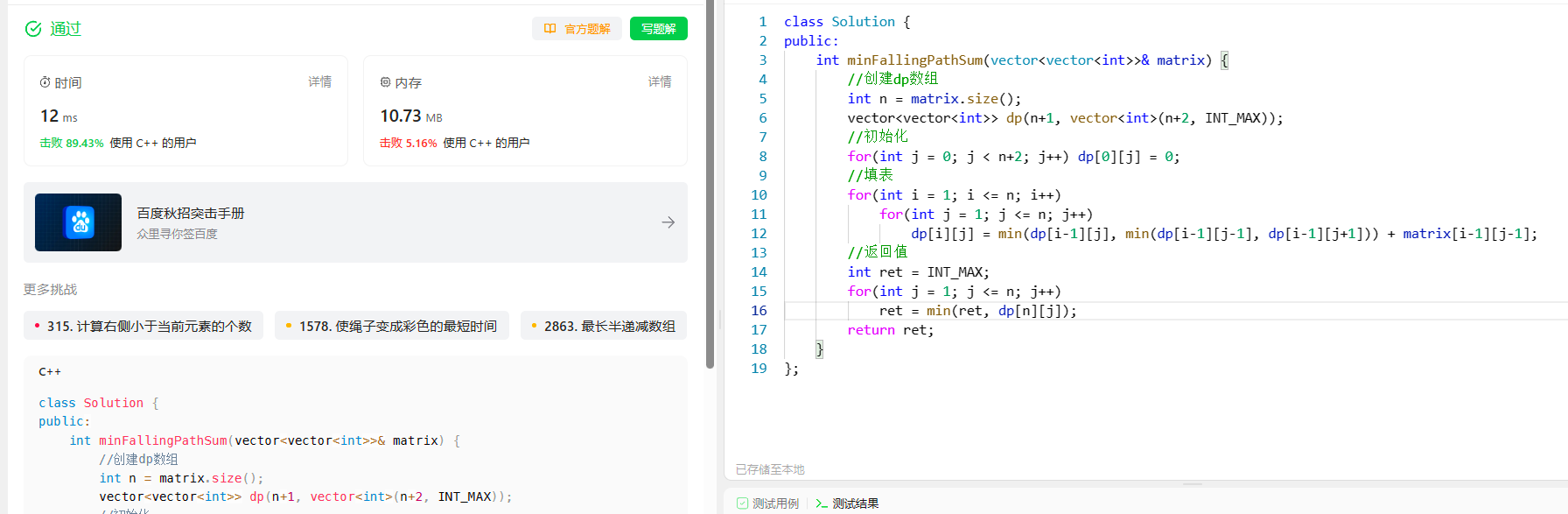
代码实现

class Solution {
public:
    int minFallingPathSum(vector<vector<int>>& matrix) {
        //创建dp数组
        int n = matrix.size();
        vector<vector<int>> dp(n+1, vector<int>(n+2, INT_MAX));
        //初始化
        for(int j = 0; j < n+2; j++) dp[0][j] = 0;
        //填表
        for(int i = 1; i <= n; i++)
            for(int j = 1; j <= n; j++)
                dp[i][j] = min(dp[i-1][j], min(dp[i-1][j-1], dp[i-1][j+1])) + matrix[i-1][j-1];
        //返回值
        int ret = INT_MAX;
        for(int j = 1; j <= n; j++)
            ret = min(ret, dp[n][j]);
        return ret;
    }
};

总结

细节1：边界情况让我们开辟dp数组时，多开辟两列 外加 一行。

细节2：初始化时和返回时，不影响逻辑和结果的位置初始化为整型最大值。