目录
一、图是什么?
二、“图”源自哪里?
三、加权图是什么?
四、有向图是什么?
五、图能给我们带来什么?
一、图是什么?
说到“图”
大部分人首先想到的是这样滴——图像

或者是
饼状图
折线图等等
其实,它们都不是!
我们所说的“图”是下面酱样子滴
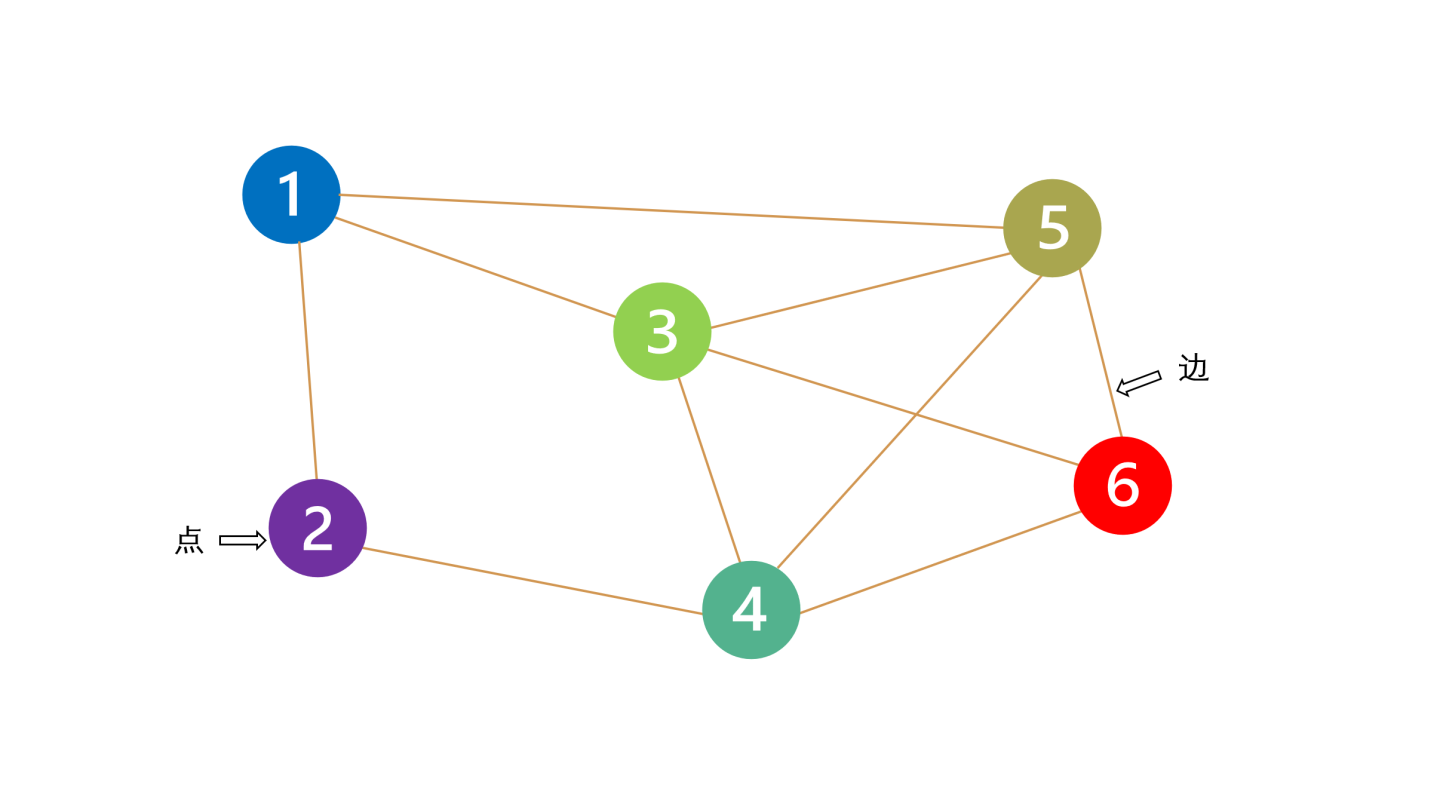
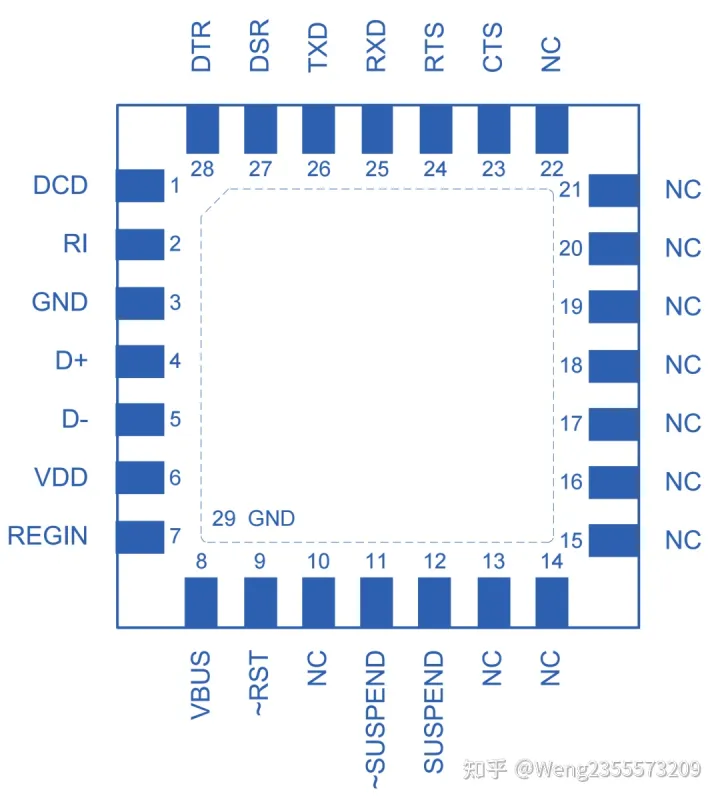
上面的数字1到数字6,都叫做“点”(或顶点)
连接点与点之间的线,叫做“边”
也就是说
由点和连接每对点的边所构成的图就叫做“图”(Graph)
点(node):称之为顶点(Vertex)或点(node),也可以称作实体(Entity)。
边(edge):连接两个点(node)的边,在知识图谱范畴内也常被称作关系(relation、relationship)。
图(Graph)用至为简洁的点与边,即可以表现出人与人、人与物、物与物之间的各种关系。
举例来说,当你查达芬奇与卢浮宫之间的关系时,你就可以关联出一张非常简单的人与物之间的图谱:
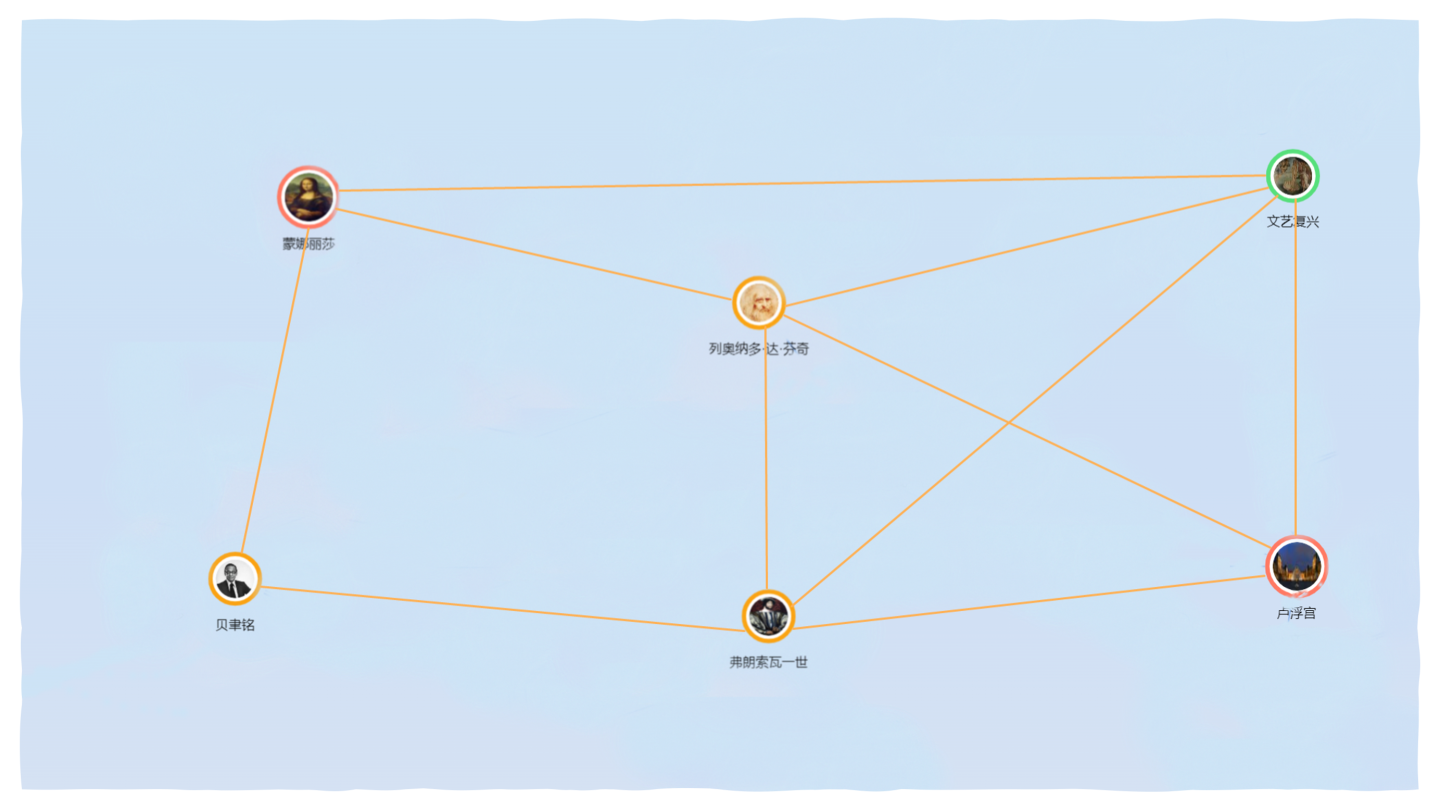
【文艺复兴(代表人物)——达芬奇——(代表作品) 蒙娜丽莎——(收藏)卢浮宫博物馆——金字塔玻璃入口(建筑师)贝聿铭——弗朗索瓦一世(收藏)——梦娜丽莎(画作)——文艺复兴(影响)】
图还可以表现出社会中的各种关系。
比如,你打算和朋友们一起跨年2023,当你有此想法时,你的脑海中会迅速地生成一张参加party的友人图谱。
同时,这张图谱还会关联出相互认识的朋友,也就是朋友的朋友的朋友…… 这就是facebook大名鼎鼎的“六度分隔理论”。
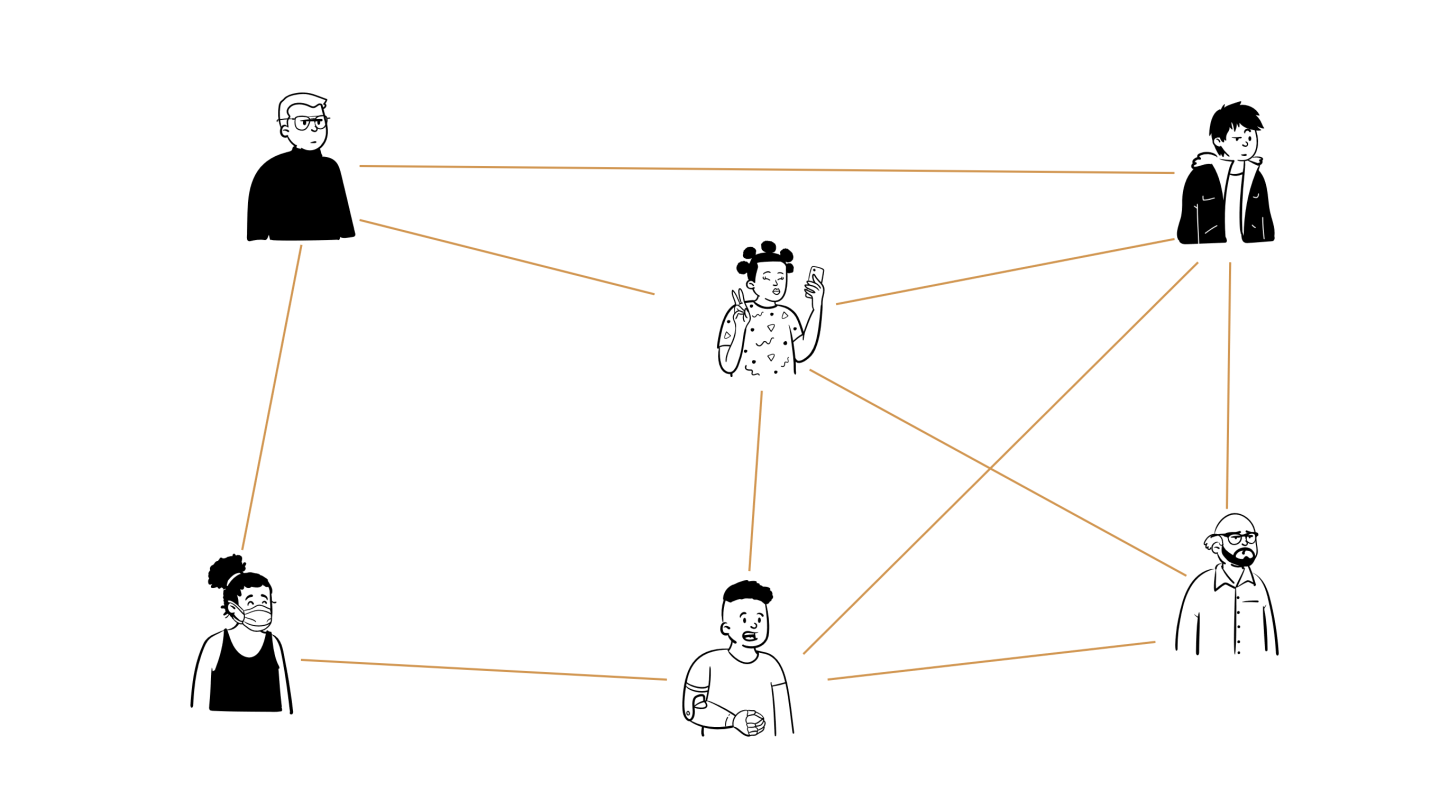
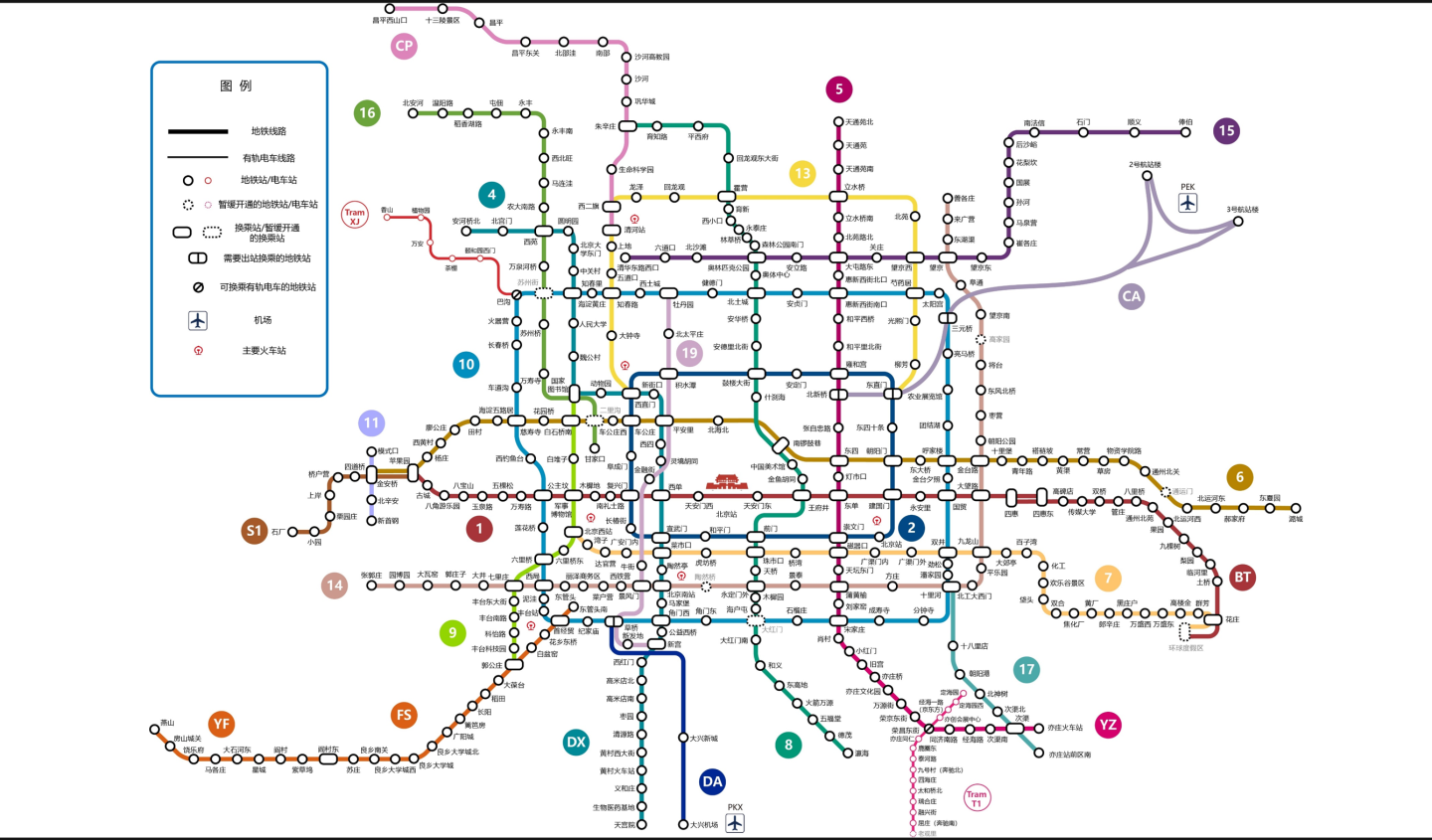
再如,我们日常生活中几乎天天都会使用的通勤工具——地铁。
如果将车站作为“点”,相邻的两站用“边”相连,那么,这也可以连成一张典型的“图”。
二、“图”源自哪里?
“图”并不是一个新生事物或新概念,反而非常地古老且传奇。
其最早起源于300年前数学家欧拉提交的一篇名为《哥尼斯堡的七座桥》的论文,这也成为图论和拓扑学最早的开端。

在欧拉之后,直到上世纪六十年代,才出现了随机图理论,也是从彼时开始,图论由纸上谈兵转为大量的实际应用和突破,比如地图染色算法、最短、最优路径计算,动态规划,社区识别等各类图算法等。
【提示:聪明的读者如果想了解更多有关“图”的前世今生,请阅读国内首本有关图的书籍——《图数据库原理、架构与应用》《图数据库原理、架构与应用》(嬴图团队)【摘要 书评 试读】- 京东图书】
三、加权图是什么?
由点和边所构成的图,还可以给边加上一个值。
这个值就叫作边的“权重”或“权”,加了权的图被称为“加权图”。
没有权的边只能表示两个点的连接状态,而有权的边就可以表示顶点之间的“连接程度”。

这个“程度”是什么意思呢?
就是根据“图”的内容不同,“程度”表示的意思也不同。
比如在地铁线路中,如果把车站与车站间的票价加在边上,就能在“图”中看出乘车费了。
四、有向图是什么?
“有向图”,顾名思义就是能表示出方向的图,我们则称为“有向图”。
与此相对,边上没有箭头表示出明确方向的图,便是“无向图”了。
有向图: 当图中的边有明确的方向时,且在图中的各类操作可以利用这种方向的时候,我们称其为有向图。例如,区块链就是典型的有向无环图,英文简称为DAG(Directed Acyclic Graph)。以DAG的方式,可以追溯每一笔比特币的流向、分布、归属。
无向图: 无向图指的是忽略了边的方向。在实际的图数据库实现中,通常都采用双向边存储的方式来实现无向图。
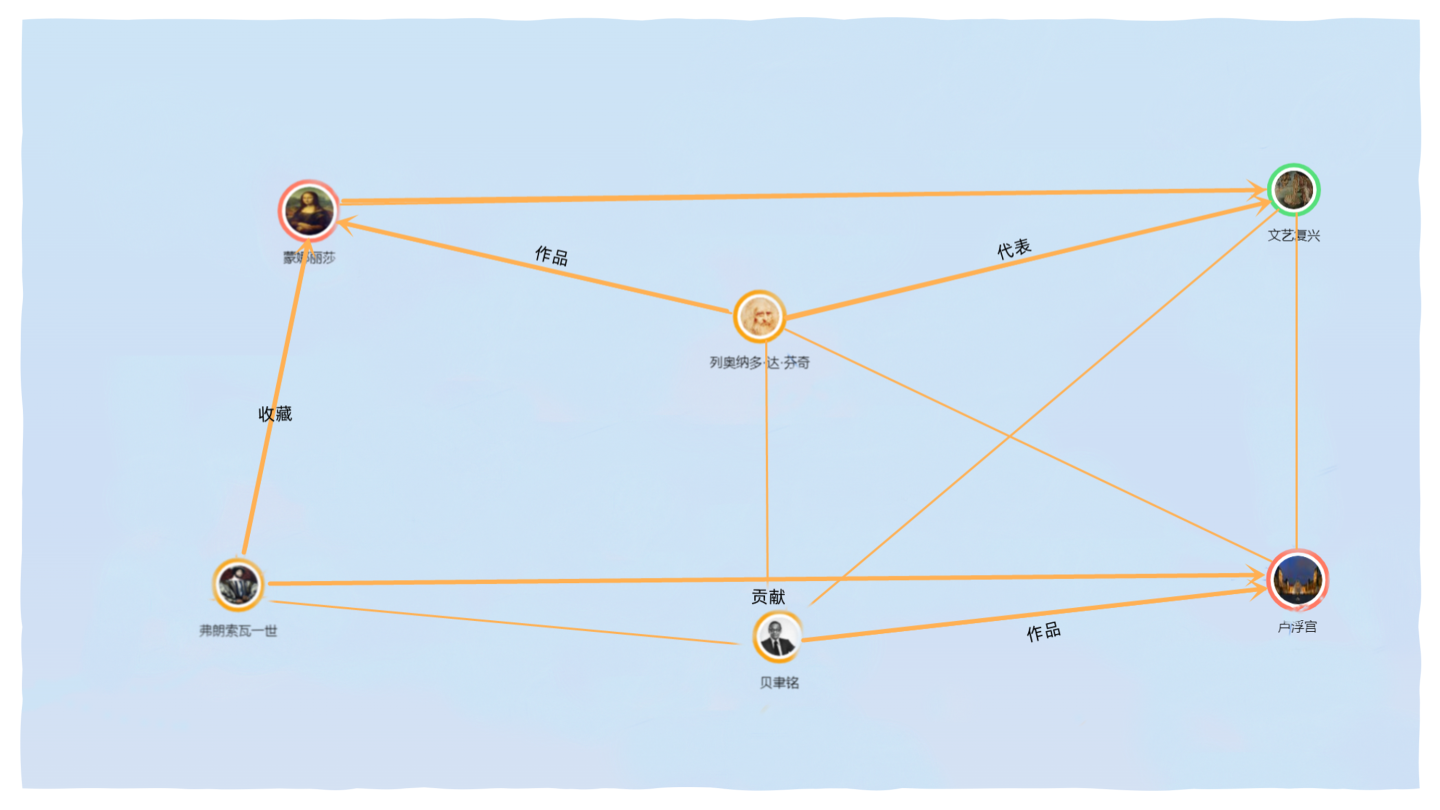
如上图所示,举世闻名的油画蒙娜丽莎的微笑出自达芬奇之手,而他也是欧洲文艺复兴的代表人物之一…… 上图中每个有明确指向箭头的图,我们就称之为有向图。
聪明的你一定能够想到,有向图是分方向的,即会分方向(左)与方向(右):
方向 (左): 表示边的方向,向左,即在图中的点的入方向,例如 a<--
方向 (右): 表示边的方向,向右,即在图中的点的出方向,例如 a-->
五、图能给我们带来什么?
想一想“图”能给我们带来了什么吧?
在进入21世纪之后,你所知道的Facebook、Google、linkedin等科技巨头,都是在使用图技术来蓬勃发展业务的。目前我们国内的企业,诸如字节跳动、华为等互联网公司,也在用该技术创新业务。当然,图算法在我们的日常生活中,亦带来很多思维上的乐趣与指引,比如你打算租房,那么如何在公司、家与交通线以及租金等问题上,达成一个和谐且节省(性价比最优)的答案呢?就可以用图来解决哦~! (文/甄参谋)