某综艺频道推出了一个闯关活动。

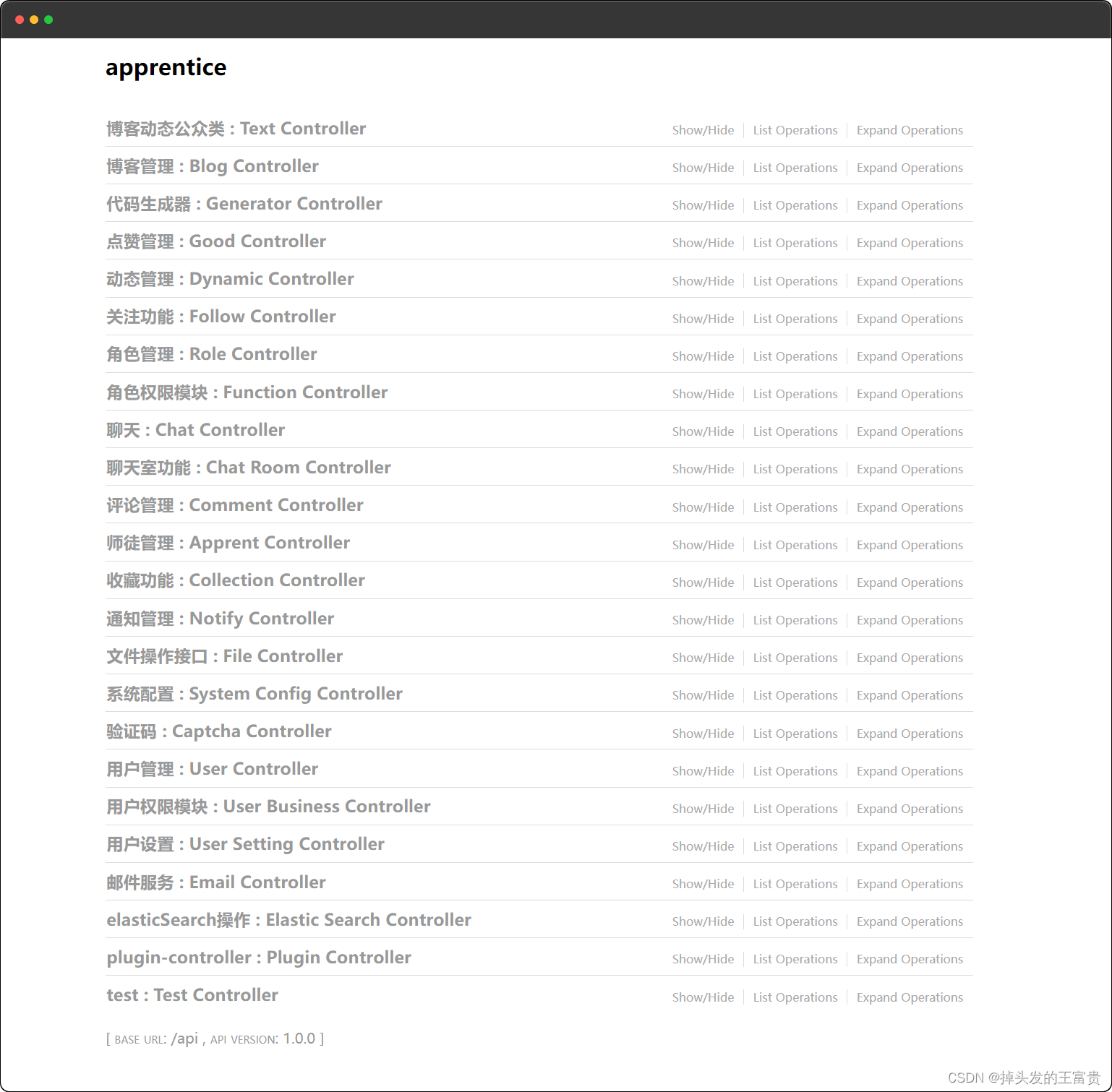
活动一共包含 n 个关卡（编号 1∼n），其中 m 个关卡为特殊关卡。

每个关卡都有一个通关分数，其中第 i 个关卡的通关分数为 ai。

挑战者可以自由决定所有关卡的具体挑战顺序，并且每通过一个关卡就可以获得该关卡的通关分数。

值得注意的是，当挑战者即将挑战的关卡是特殊关卡时，如果挑战者当前已经获得的总分数大于该特殊关卡的通关分数，则挑战者可以对该关卡的通关分数进行一次修改，修改后的新分数不能小于原分数，也不能大于挑战者当前已经获得的总分数。

请你计算并输出挑战者通过所有关卡获得的总分数的最大可能值。

输入格式

第一行包含两个整数 n,m。

第二行包含 n 个整数a1,a2,…,an，表示每个关卡的通过分数。

第三行包含 m 个整数 b1,b2,…,bm，表示每个特殊关卡的编号。

输出格式

一个整数，表示挑战者通过所有关卡获得的总分数的最大可能值。

保证最终答案不超过 2^63−1。(本质就是不超过long  long)

数据范围

前 4 个测试点满足 1≤n≤4。
所有测试点满足 1≤n,m≤100，m≤min(n,30)，1≤ai≤107，1≤bi≤n，bi 两两不同。

输入样例1：

4 1
1 3 7 5
3

输出样例1：

18

输入样例2：

3 2
10 3 8
2 3

输出样例2：

40

输入样例3：

2 2
100 200
1 2

输出样例3：

400

输入样例4：

1 1
1
1

输出样例4：

1

 证明：我最初的想法是：所有普通关卡分值累加后，将特殊关卡从小到大排序，然后从左往右判断，如果当前关卡分值小于总分值时，总分值乘以2，否则去末尾加上末尾的分值。

首先说一下我之前的想法为什么是错的，如果当前分值乘以2后，还没有末尾最大的分值大，此时也丧失了一次乘2的机会，如果先加末尾的值，再乘以2，分值会更大

 附上y总证明的图：令从小到大排序的为Z轴，从大到小排序的为Y轴,公式为算前两项的值

首先可以看出 Z1 = Y1

因为xi<xj        Z2 <= Y2

又从前两步可以看出  Z3 <= Y3 , Z4 < Y3

综上所述，从大到小排序可以保证值最大。

代码

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 110;
typedef unsigned long long ULL;

int a[N],book[N],b[N],c[N];

int main()
{
    int n,m;
    cin>>n>>m;
    
    for(int i=1;i<=n;i++)
    cin>>a[i];
    
    while(m--)
    {
        int x;
        cin>>x;
        book[x]=1;
    }
    
    ULL res=0;
    for(int i=1;i<=n;i++)
       if(!book[i]) res=res+a[i];
       
    int y=1;
    for(int i=1;i<=n;i++)
    {
        if(book[i])
        {
            b[y++]=a[i];
        }
    }
    sort(b+1,b+y);
    for(int j=y-1;j>=1;j--)
    {
        if(res>b[j])
        {
            res*=2;
        }
        else res=res+b[j];
    }
    
    cout<<res<<endl;
    return 0;
}