算法的复杂性分析

---

---

0、 算法评价的基本原则

评价一个算法的好坏实际就是评价一个程序的好坏。通常一个好的算法应该应考虑达到以下目标。

1.正确性（correctness）

一个好的算法的前提就是算法的正确性。不正确的算法没有任何意义。

2 可读性（Readability）

算法主要是为了人的阅读与交流，其次才是机器的执行。

3.健壮性（Robustness）和可靠性

• 健壮性是指当输入数据非法时，算法也能适当地做出反应或进行处理。

• 正确性和健壮性是相互补充的。

• 程序的可靠性指一个程序在正常情况下能正确地工作，而在异常情况下也能做出适当处理。

4. 效率（efficiency）

• 效率包括运行程序所花费的时间以及运行这个程序所占用的资源(占用的存储空间 )。算法应该有效使用存储空间，并具有高的时间效率。

• 对于规模较大的程序，算法的效率问题是算法设计必须面对的一个关键问题，目标是设计复杂性尽可能低的算法。

5. 简明性（simplicity）

• 算法应该思路清晰、层次分明、容易理解、利于编码和调试，即算法简单，程序结构简单。

• 简单的算法效率不一定高，要在保证一定效率的前提下力求得到简单的算法。

6. 最优性（optimality）

• 指求解某类问题中效率最高的算法。最优性与所求问题自身的复杂程度有关。

1、影响程序运行时间的因素

• 程序所依赖的算法

求解同一个问题的不同算法，其程序运行时间一般不同。

• 问题的规模和输入数据

程序的一次运行是针对所求解问题的某一特定实例而言的。因此分析算法性能需要考虑的一个基本问题是所求解问题实例的规模，即输入数据量，必要时也考虑输出的数据量。

• 计算机系统的性能

算法运行所需要的时间还依赖于计算机的硬件系统和软件系统。

2、算法复杂度

算法的复杂度主要包括时间复杂度和空间复杂度。

2.1 算法的时间复杂度

算法的时间复杂度指算法运行所需时间，也指执行算法所需要的计算工作量。

• 度量算法的工作量

一个算法是由基本运算和控制结构（顺序、选择、循环）构成的，则算法执行时间取决于两者的综合效果。

通常的做法是：从算法中选取一种对于所研究的问题来说是基本的运算，以该基本运算重复执行的次数作为算法的工作量。

例如：在考虑两个矩阵相乘时，可以将两个实数之间的乘法运算作为基本运算，而对于所用的加法（或减法）运算可以忽略不计。

• 算法所执行的基本运算次数还与问题的规模有关。例如：两个20阶矩阵相乘与两个3阶矩阵相乘所需要的基本运算（即两个实数的乘法）次数显然是不同的。前者需要更多的运算次数，因此，在分析算法的工作量时，还必须对问题的规模进行度量。

综上所述，算法的工作量用算法所执行的基本运算次数来度量，而算法所执行的基本运算次数是问题规模的函数。即算法的工作量=f(n)，n是问题的规模。

• 算法的执行时间绝大部分花在循环和递归上

对于循环语句的时间代价一般用以下三条原则分析：

1）对于一个循环，循环次数乘以每次执行简单语句的数目即为其时间代价。

2）对于多个并列循环，可先计算每个循环的时间代价，然后按加法规则计算总代价。

3）对于多层嵌套循环，一般可按乘法规则计算。但如果嵌套是有条件的，为精确计算其时间代价，要仔细累加循环中简单语句的实际执行数目，以确定其时间代价。

2.2 渐进表示法

一般来说，当N单调增加且趋于∞时，T(N)也将单调增趋于∞。对于T(N)，如果存在函数T’(N)，使得当N→∞时有(T(N)-T’(N))/T(N)→0，那么我们就说T’(N)是T(N)当N→∞时的渐进性态。在数学上，T’(N)是T(N)当N→∞时的渐进表达式。例如：3N²+4NlogN+7与3N2, 3N²是3N²+4NlogN+7的渐近表达式。

算法复杂性在渐近意义下的记号有：O、Ω、Θ等，分别表达运行时间的上界、运行时间的下界、运行时间的准确界等

2.2.1 运行时间的上界

设函数f(n)和g(n)是定义在非负整数集合上的正函数，如果存在正整数n0和正常数c，使得当n≥n0时，有f(n)≤cg(n)，就称f(n)的阶至多是O(g(n))，记做f(n) = O(g(n))，称为大O记号（big O notation）。如图所示。

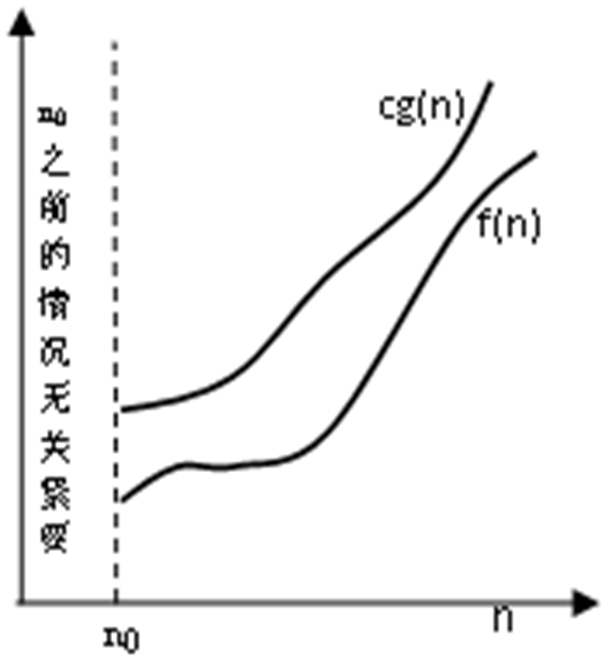
例如

• f(n) = 2n²+3，g(n)=n²

当n≥3时，2n²+3≤3*n²，所以，可选c=3，n0 = 3。对于n≥n0，f(n)= 2n²+3≤3n²，所以，f(n) = O(n²)，即2n²+3=O(n²)。

• f(n) = n！= O(nⁿ)

对于n≥1，有n(n-1)(n-2) … 1≤nⁿ，因此，可选c=1，n0=1。对于n≥n0，f(n)= n!≤nⁿ，所以，f(n) = O(nⁿ)。

• 10n² + 9≠O(n)

使用反证法，假定存在c和n0，使得对于n≥n0，10n² + 9≤cn始终成立，那么有10n + 9/n≤c，即n≤c/10-9/(10n)总成立。但此不等式不可能总成立，取n=c/10+1时，该不等式便不再成立。

定理1： 如果f(n)=a_mn^m+a_m-1n^m-1+…+a₁nn+a₀是m次多项式，且am＞0，则f(n)=O(n^m)。

证明如下：

• 规则

加法规则

O(f(n))+O(g(n))=O(max(f(n),g(n)))
O(f(n))+O(g(n))=O(f(n)+g(n))

如果g(n)=O(f(n))，则O(f(n))+O(g(n))=O((f(n))

乘法规则

O(f(n))*O(g(n))=O(f(n)*g(n))
O(c*f(n))=O(f(n))，c是一个正常数
f(n)=O((f(n))

2.2. 运行时间的下界

设有函数f(n)和g(n)是定义在非负整数集合上的正函数，如果存在正整数n0和正常数c，使得当n≥n0时，有f(n)≥cg(n)，就称f(n)的阶至少是Ω(g(n))，记做f(n) = Ω(g(n))，称为Ω记号（omega notation）。如图所示。

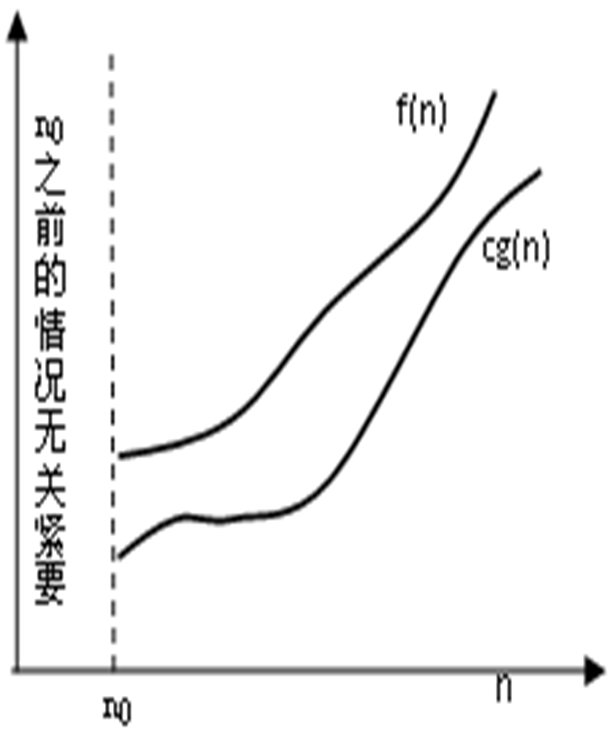
这个定义的意义是：当n充分大时有下界，且g(n)是它的一个下界，f(n)的增长至少像g(n)那样快。它用以表示一个算法运行时间的下界。

示例

定理2：如果f(n)=a_mn^m+a_m-1n^m-1+…+a₁nn+a₀是m次多项式，且am＞0，则f(n)=Ω(n^m)。

2.2.3 运行时间的准确界

设有函数f(n)和g(n)是定义在非负整数集合上的正函数，如果存在正整数n0和正常数c1和c2（c1 ≤c2），使得当n≥n0时，有c1 g(n)≤f(n)≤c2 g(n) ，就称f(n)的阶是Θ(g(n))，则记做f(n)=Θ(g(n))，称为Θ记号（Theta notation）。
如图所示。

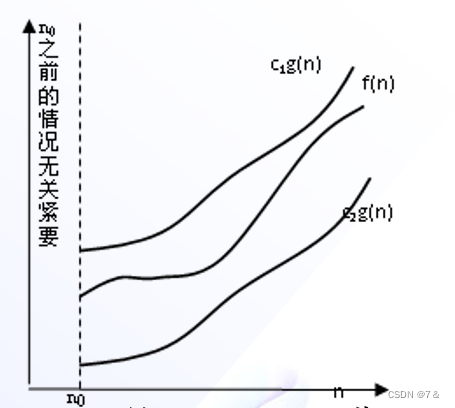
即f(n)=Θ(g(n))当且仅当f(n)=O(g(n))且f(n)=Ω(g(n))，此时称f(n)与g(n)同阶。这个定义的意义是：f(n)的增长像g(n)一样快。

• 示例

3、总结

算法按时间复杂度分类

• 常见的复杂度类型如下：

1＜loglogn＜logn＜n^(1/2)＜n^(3/4)＜n＜nlogn＜n^2＜2^n＜n!＜2^(n^2)

凡渐近时间复杂度有多项式时间限界的算法称作多项式时间算法（polynomial time algorithm），而渐近时间复杂度为指数函数限界的算法称作指数时间算法（exponential time algorithm）。

• 最常见的多项式时间算法的渐近时间复杂度。

O(1)＜O(log n)＜O(n)＜O(nlog n)＜O(n^2)＜O(n^3)

• 最常见的指数时间算法的渐近时间复杂度。

O(2^n)＜O(n!)＜O(n^n)

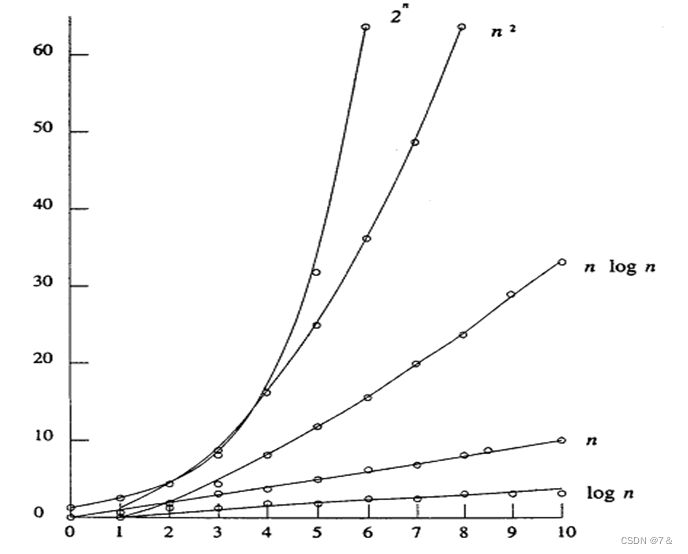
随着n的增大，算法在所需时间上非常悬殊。如图所示。

4、参考

• 算法设计与分析（第4版）

结束！