文章目录
- 一、KNN 简介
- 二、KNN 核心思想
- 实例
- 分析:K 值的影响
- 三、KNN 的关键
- 1. 距离计算
- 1. 闵可夫斯基距离
- 2. 曼哈顿距离
- 3. 欧氏距离
- 4. 切比雪夫距离
- 5. 余弦距离
- 总结
- 2. K值选择
- 四、KNN 的改进:KDTree
- 五、KNN 回归算法
- 参考链接
一、KNN 简介
KNN 算法,或者称 k-最近邻算法,是 有监督学习 中的 分类算法 。它可以用于分类或回归问题,但它通常用作分类算法。
二、KNN 核心思想
KNN 的全称是 K Nearest Neighbors,意思是 K 个最近的邻居。该算法用 K 个最近邻来干什么呢?其实,KNN 的原理就是:当预测一个新样本的类别时,根据它距离最近的 K 个样本点是什么类别来判断该新样本属于哪个类别(多数投票)。
实例
图中绿色的点是待预测点,假设 K=3。那么 KNN 算法就会找到与它距离最近的三个点(这里用圆圈把它圈起来了),然后看这三个点中哪种类别多一些,比如这个例子中是蓝色三角形多一些,新来的绿色点就被归类到蓝三角了。
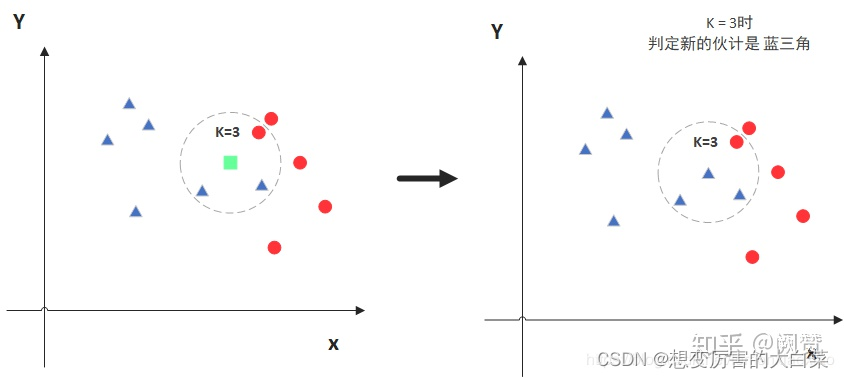
但是,当 K=5 的时候,判定就变得不一样了。这次变成红圆多一些,所以新来的绿点被归类成红圆。从这个例子中,我们就能看得出 k 值的确定对KNN算法的预测结果有着至关重要的影响。
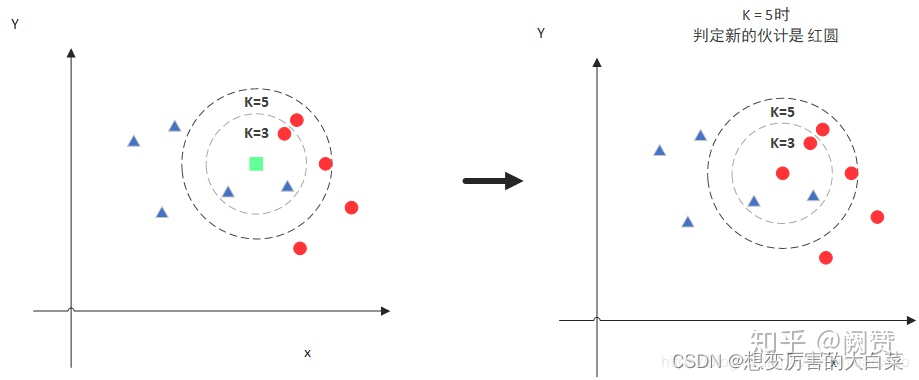
分析:K 值的影响
如果k值比较小,相当于我们用较小的领域内的训练样本对实例进行预测。这时,算法的近似误差(Approximate Error)会比较小,因为只有与输入实例相近的训练样本才会对预测结果起作用。但是,它也有明显的缺点:算法的估计误差比较大,预测结果会对近邻点十分敏感,也就是说,如果近邻点是噪声点的话,预测就会出错。因此,k值过小容易导致KNN算法的过拟合。
同理,如果k值选择较大的话,距离较远的训练样本也能够对实例预测结果产生影响。这时候,模型相对比较鲁棒,不会因为个别噪声点对最终预测结果产生影响。但是缺点也十分明显:算法的近邻误差会偏大,距离较远的点(与预测实例不相似)也会同样对预测结果产生影响,使得预测结果产生较大偏差,此时模型容易发生 欠拟合。
因此,在实际工程实践中,我们一般采用交叉验证的方式选取 k 值(以下第三节会介绍)。通过以上分析可知,一般 k 值选得比较小,我们会在较小范围内选取 k 值,同时把测试集上准确率最高的那个确定为最终的算法超参数 k 。
三、KNN 的关键
实际上,KNN 算法有两个关键点:1. 点之间距离的计算;2. K 值的选取。
1. 距离计算
样本空间内的两个点之间的距离量度表示两个样本点之间的相似程度:距离越短,表示相似程度越高;反之,相似程度越低。
常用的距离量度方式包括:
- 闵可夫斯基距离
- 曼哈顿距离
- 欧氏距离
- 切比雪夫距离
- 余弦距离
1. 闵可夫斯基距离
闵可夫斯基距离本身不是一种距离,而是一类距离的定义。对于n维空间中的两个点x(x1,x2,…,xn)和y(y1,y2,…,yn),x和y之间的闵可夫斯基距离可以表示为:
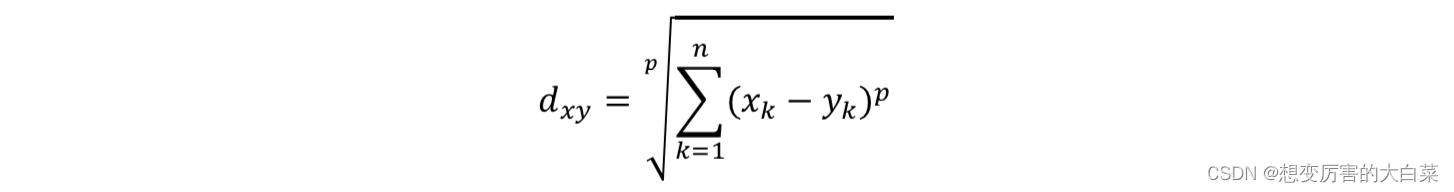
其中,p是一个可变参数:
- 当p=1时,被称为曼哈顿距离;
- 当p=2时,被称为欧氏距离;
- 当p=∞时,被称为切比雪夫距离。
2. 曼哈顿距离
根据闵可夫斯基距离定义,曼哈顿距离的计算公式可以写为:
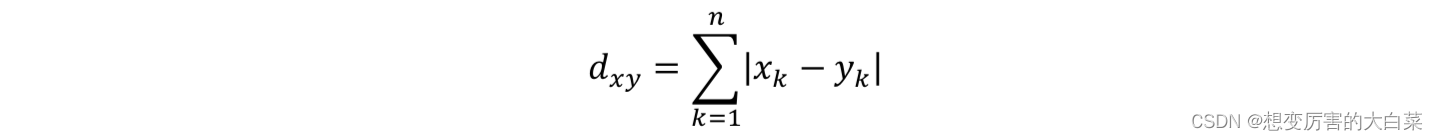
它测量两点之间的绝对值。
3. 欧氏距离
根据以上定义,欧氏距离可以写为:
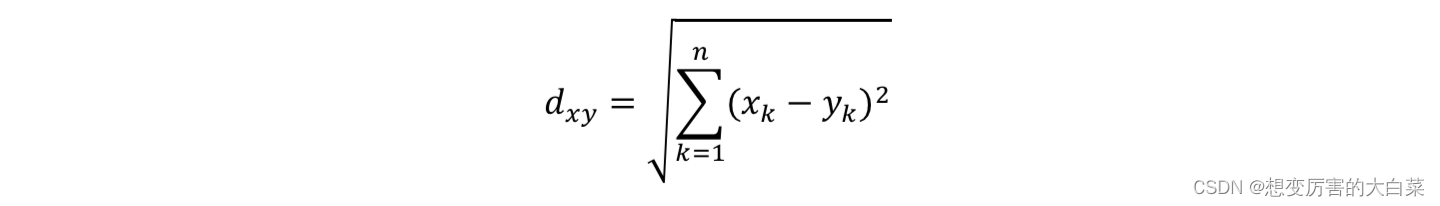
欧氏距离(L2范数)是最易于理解的一种距离计算方法,源自欧氏空间中两点间的距离公式,也是最常用的距离量度。它测量两点之间的直线距离。
通常 KNN 算法中使用的是欧式距离。
4. 切比雪夫距离
切比雪夫距离是将2个点之间的距离定义为其各坐标数值差的最大值。对应L∞范数:

5. 余弦距离
余弦相似度的取值范围是[-1,1],相同两个向量的之间的相似度为1。
余弦相似度的定义公式为 :

余弦距离的取值范围是[0,2]:

总结
这样我们就明白了如何计算距离。KNN 算法最简单粗暴的就是将预测点与所有点距离进行计算,然后保存并排序,选出前面 K 个值看看哪些类别比较多。但其实也可以通过一些数据结构来辅助,比如最大堆、KDTree,能够减小计算量,从而快速找到 K 个最近邻。
2. K值选择
通过上面那张图我们知道 K 的取值比较重要,那么该如何确定 K 取多少值好呢?答案是通过交叉验证(将样本数据按照一定比例,拆分出训练用的数据和验证用的数据,比如6:4拆分出部分训练数据和验证数据),从选取一个较小的 K 值开始,不断增加 K 的值,然后计算验证集合的方差,最终找到一个比较合适的 K 值。
通过交叉验证计算方差后你大致会得到下面这样的图:
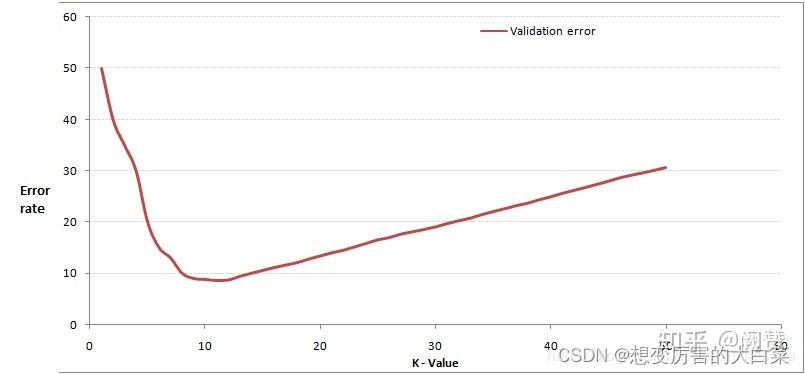
这个图其实很好理解,当你增大 K 的时候,一般错误率会先降低,因为有周围更多的样本可以借鉴了,分类效果会变好。但是,K值太大的时候就会失去意义:这也很好理解,比如说你一共就35个样本,当你 K 增大到30的时候,KNN 基本上就没意义了。
所以选择 K 点的时候可以选择一个较大的临界 K 点,当它继续增大或减小的时候,错误率都会上升,比如图中的 K=10。
四、KNN 的改进:KDTree
KNN 算法最简单粗暴的就是将预测点与所有点距离进行计算,然后保存并排序,选出前面 K 个值看看哪些类别比较多。这样的直接暴力寻找的方法,在特征空间维度不高且训练样本容量小时,是可行的,但是当特征空间维度特别高或者样本容量较大时,计算过程就会非常耗时,这种方法就不可行了。
因此,为了快速查找到 k 个近邻,我们可以考虑使用特殊的数据结构存储训练数据,用来减少搜索次数。其中,KDTree就是最著名的一种。
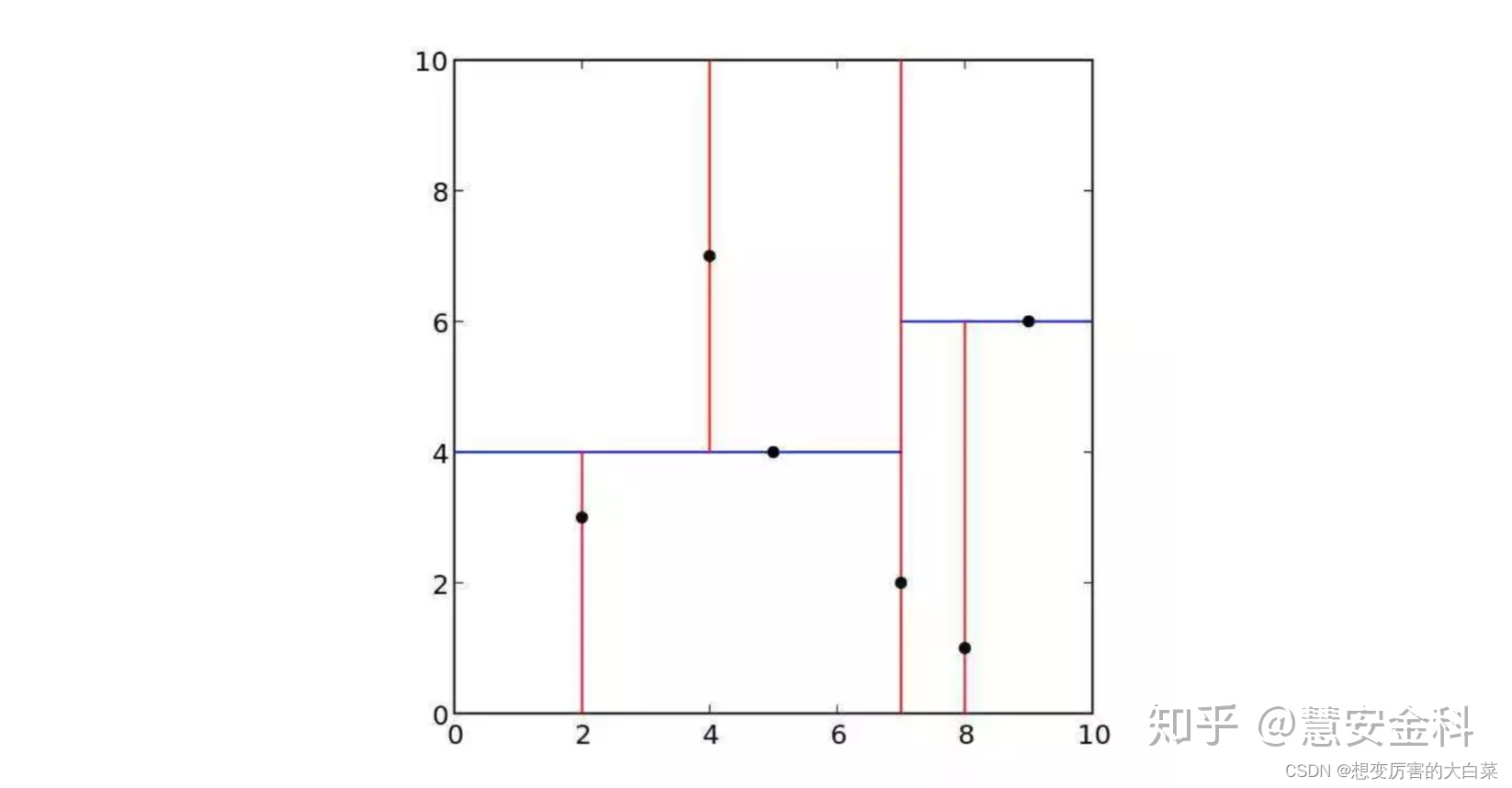
KDTree(K-dimension Tree)是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。KDTree是一种二叉树,表示对k维空间的一种划分构造KDTree相当于不断地利用垂直于坐标轴的超平面将k维空间进行切分,构成一系列的k维超矩形区域。KDTree的每个节点对应于一个k维超矩形区域。利用KDTree可以省去对大部分数据点的搜索,从而减少搜索的计算量。
关于 KDTree 的详细介绍,请参考我的另一篇文章:【KNN分类】kd-tree
五、KNN 回归算法
上文所述的 KNN 算法主要用于分类,实际上,KNN算法也可以用于回归预测。接下来,我们讨论一下KNN算法如何用于回归。
与分类预测类似,KNN算法用于回归预测时,同样是寻找新来的预测实例的 k 近邻,然后对这 k 个样本的目标值取 均值 即可作为新样本的预测值:
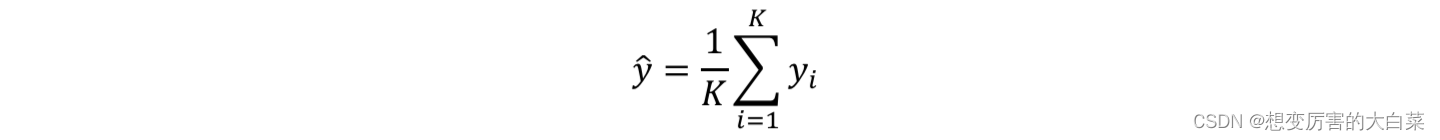
参考链接
- Python—KNN分类算法(详解)
- 什么是KNN算法?