定量qₐ是一个值，它将一组给定的数字进行划分，其中 α * 100%的数字小于该值，(1-α) * 100%的数字大于该值。

统计中经常使用 α = 0.25、α = 0.5 和 α = 0.75 的四分位数 qₐ，称为四分位数。这些四分位数分别称为 Q₁、Q₂ 和 Q₃。三个四分位数将数据分成 4 个相等的部分。

同样，还有百分位数 p，它将一组给定的数字平均分成 100 份。百分位数用 pₐ 表示，其中 α 是小于相应值的数字的百分比。

四分位数 Q₁、Q₂ 和 Q₃ 分别对应百分位数 p₂₅、p₅₀ 和 p₇₅。

在下面的示例中，对于一组给定的数字，可以找到所有三个四分位数。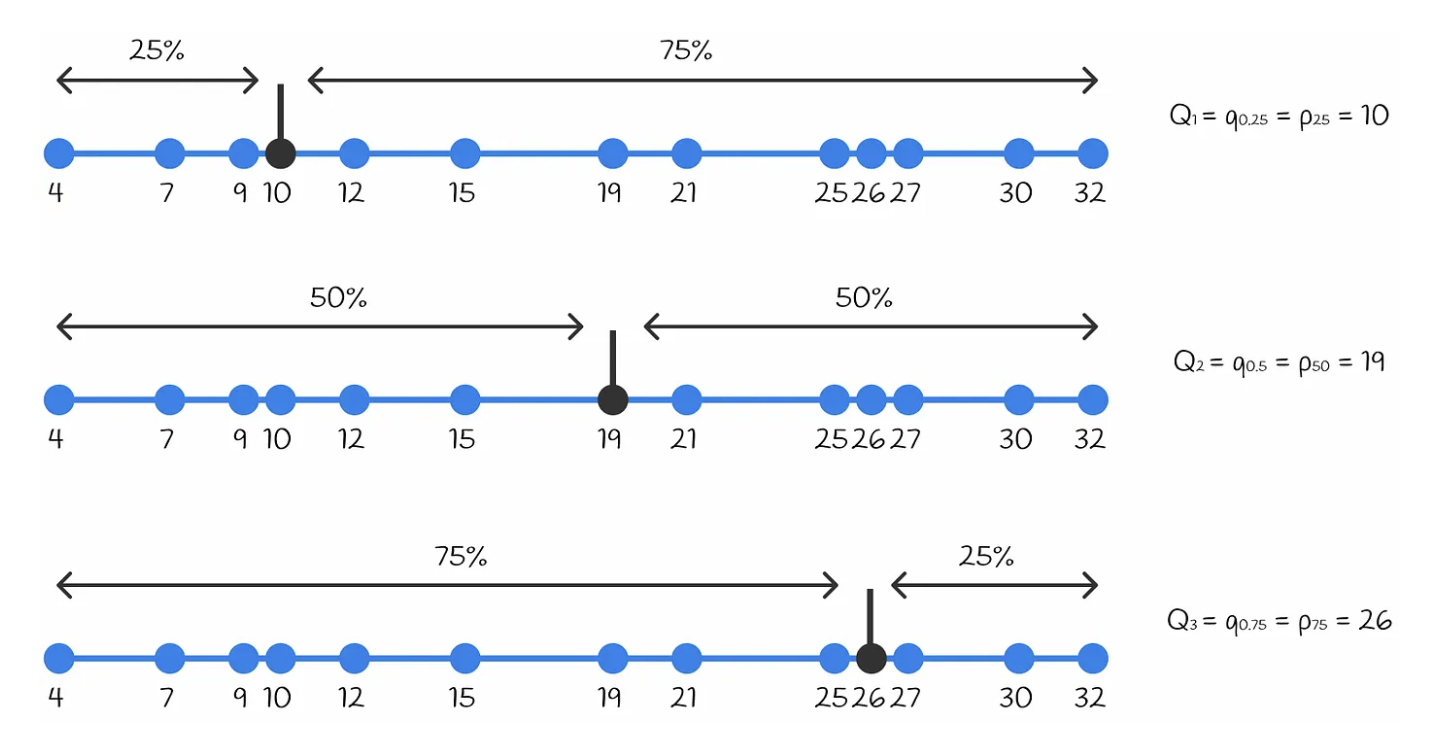

Quantile Loss

旨在预测特定变量量值的机器学习算法使用量值损失作为损失函数。在介绍算法之前，让我们先看一个简单的例子。

设想一个问题，其目标是预测变量的 75th 百分位数。 事实上，这句话等同于预测误差在 75% 的情况下必须为负，而在另外 25% 的情况下必须为正。这就是量值损失背后的实际直觉。

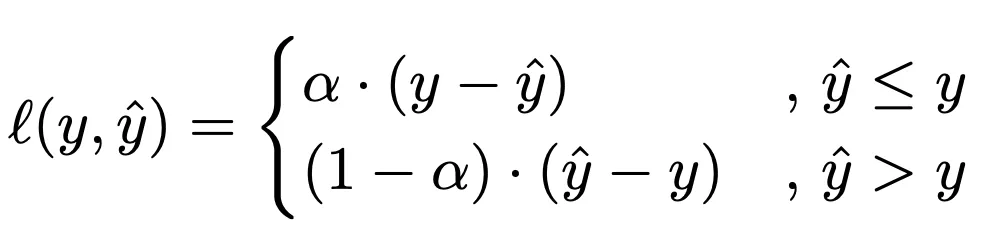
量化损失的值取决于预测值是小于还是大于真实值。为了更好地理解其背后的逻辑，假设我们的目标是预测 80 分位数，因此将 α = 0.8 的值插入公式中。结果，公式如下

基本上，在这种情况下，量值损失对低估预测的惩罚是高估预测的 4 倍。这样，模型对低估误差的影响会更大，预测值也会更高。因此，拟合模型平均在大约 80% 的情况下会高估结果，在 20% 的情况下会低估结果。

现在，假设对同一目标进行了两次预测。目标值为 40，而预测值分别为 30 和 50。让我们计算两种情况下的量化损失。尽管两种情况下 10 的绝对误差相同，但损失值却不同：

for 30, the loss value is l = 0.8 * 10 = 8
for 50, the loss value is l = 0.2 * 10 = 2.

下图显示了当真实值为 40 时，不同参数 α 的损失值。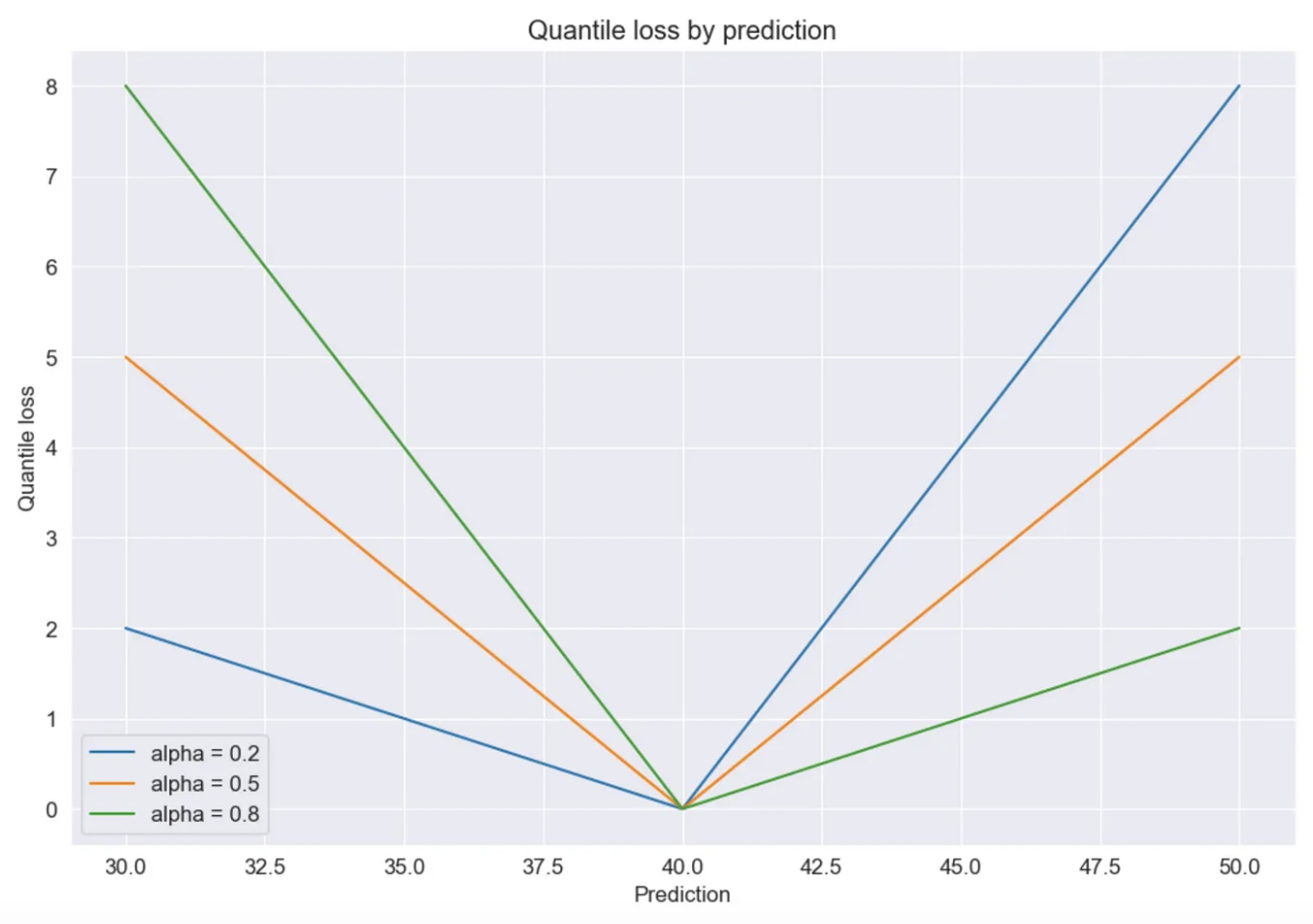

预测某个变量的量化值的问题称为量化回归。

示例

让我们创建一个包含 10 000 个样本的合成数据集，根据游戏时长来估算玩家在视频游戏中的评分。

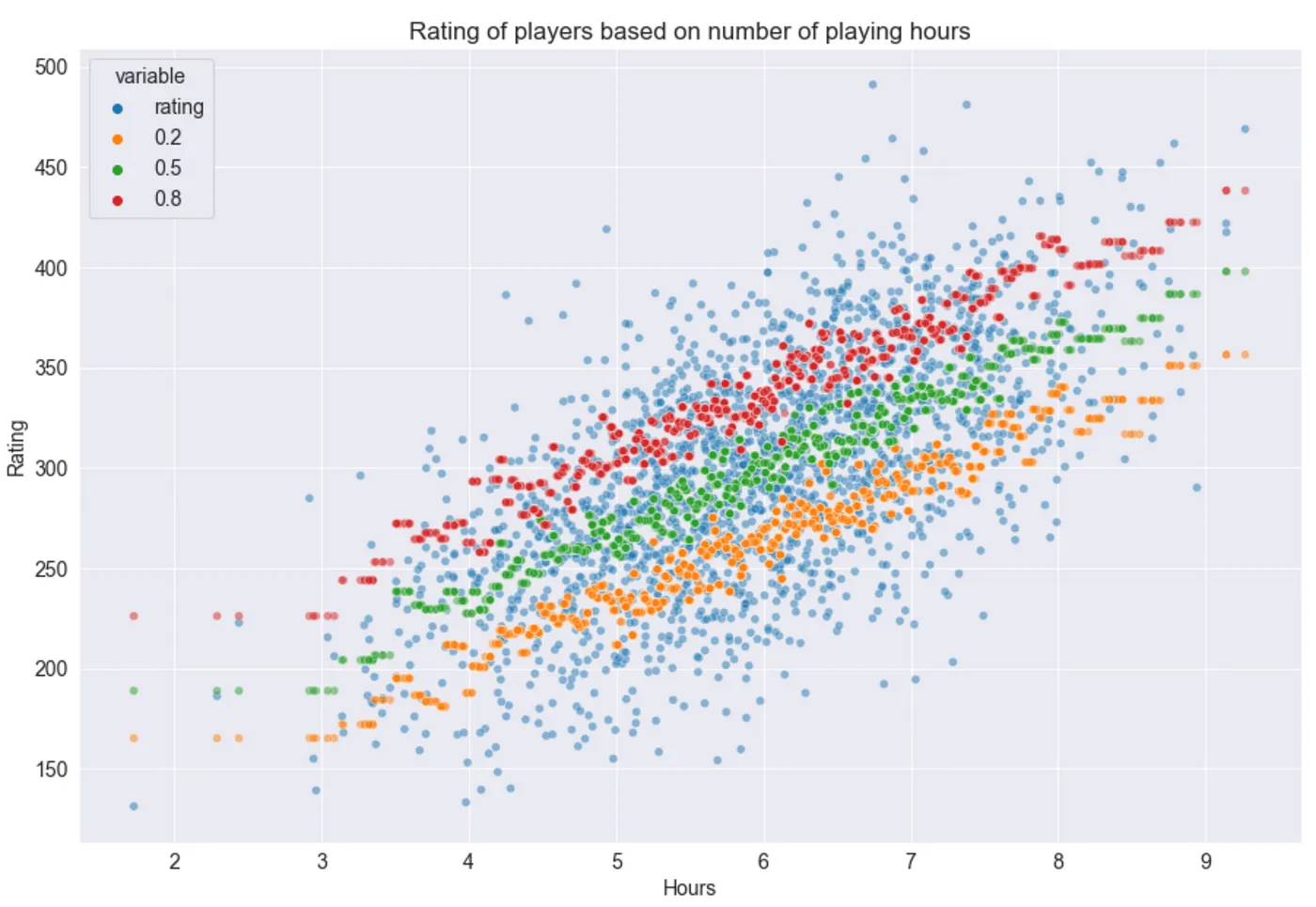
从上面的散点图可以看出，α 值越大，模型产生的高估结果越多。此外，让我们比较一下每个模型与所有目标值的预测结果。

我们可以清楚地看到输出结果的模式：对于任意 α 值，预测值在大约 α * 100% 的情况下都大于真实值。因此，我们可以通过实验得出结论：我们的预测模型工作正常。