代码随想录系列文章目录

动态规划篇 —— 区间dp

---

647. 回文子串

题目链接
回文子串还是很难的我觉得，所以应该多做几遍
这道题的dp数组代表就不是问题里问的回文子串的数目，而是这段是不是回文，需要额外一个计数器来统计数目

1.状态定义

布尔类型的dp[i][j]：表示区间范围[i,j] （注意是左闭右闭）的子串是否是回文子串，如果是dp[i][j]为true，否则为false。

2.状态转移

整体上是两种，就是s[i]与s[j]相等，s[i]与s[j]不相等这两种。

当s[i]与s[j]不相等，那没啥好说的了，dp[i][j]一定是false。

当s[i]与s[j]相等时，这就复杂一些了，有如下三种情况

情况一：下标i 与 j相同，同一个字符例如a，当然是回文子串
情况二：下标i 与 j相差为1，例如aa，也是回文子串
情况三：下标：i 与 j相差大于1的时候，例如cabac，此时s[i]与s[j]已经相同了，我们看i到j区间是不是回文子串就看aba是不是回文就可以了，那么aba的区间就是 i+1 与 j-1区间，这个区间是不是回文就看dp[i + 1][j - 1]是否为true。

if s[i] != s[j]: dp[i][j] = False
else:
	if j - i <= 1:
    	dp[i][j] = True
        cnt += 1
    elif dp[i+1][j-1]:
    	dp[i][j] = True
        cnt += 1

3.base case

这道题开的数组是高宽都是n的，没有特殊的base case
初始化全为False就行

4.遍历顺序以及解的位置

由dp[i+1][j-1]， 遍历顺序i是反序的，j是正序的

解的位置就是计数器的值

class Solution:
    def countSubstrings(self, s: str) -> int:
        n = len(s)
        dp = [[False] * n for _ in range(n)]
        cnt = 0
        for i in range(n-1, -1, -1):
            for j in range(i, n):
                if s[i] != s[j]: dp[i][j] = False
                else:
                    if j - i <= 1:
                        dp[i][j] = True
                        cnt += 1
                    elif dp[i+1][j-1]:
                        dp[i][j] = True
                        cnt += 1
        return cnt

516.最长回文子序列

题目链接

这道题和上面的不同在于这道题是子序列，不需要连续
第二个区别是求的最长的，我们可以把dp数组的状态定义为长度

1.状态定义

dp[i][j]：字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。

这道题代码里我开的还是n行n列的数组，正好映射到s的下标那种

2.状态转移

在判断回文子串的题目中，关键逻辑就是看s[i]与s[j]是否相同

如果s[i]与s[j]相同，那么dp[i][j] = dp[i + 1][j - 1] + 2;

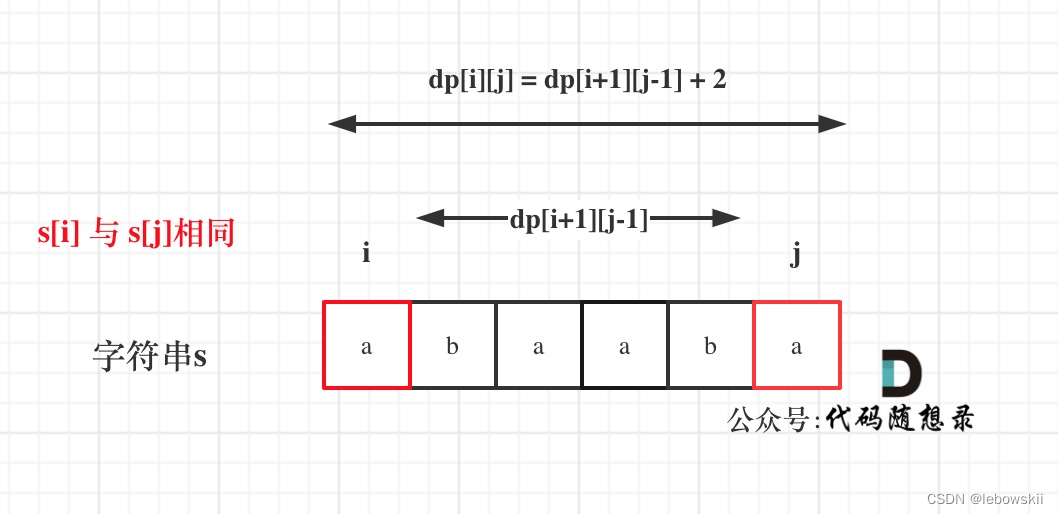
但是这题来说，j可不是从i开始，子串那题，我们j是从i开始，是因为有 a 这种单个字母需要被判回文子串的情况，而这个需要统计的是长度；我们j从i+1开始遍历

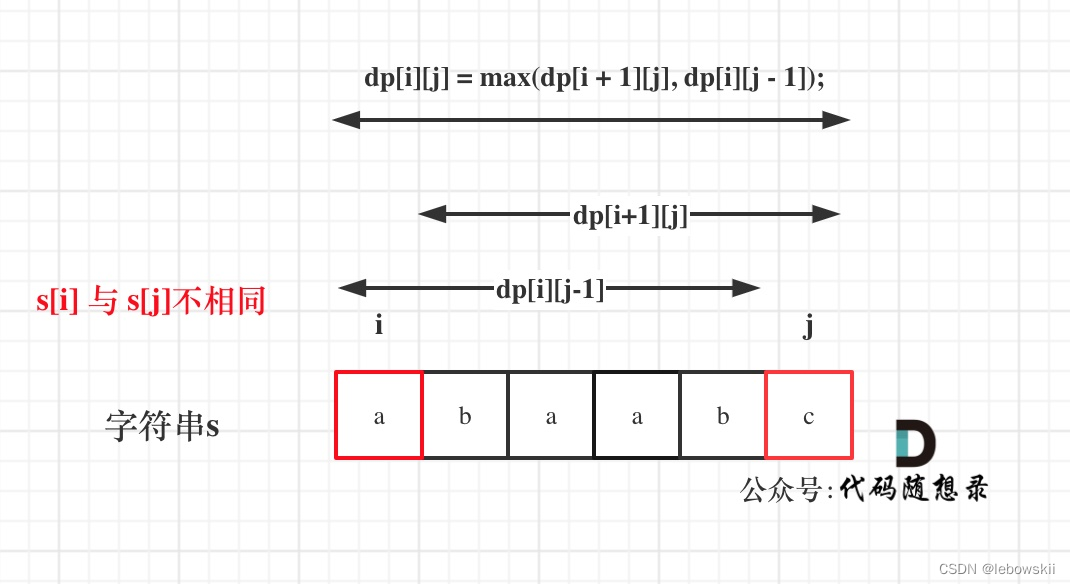
如果s[i]与s[j]不相同，说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子串的长度，那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。

加入s[j]的回文子序列长度为dp[i + 1][j]。

加入s[i]的回文子序列长度为dp[i][j - 1]。

那么dp[i][j]一定是取最大的，即：dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);

3.base case

由于上面我说的i j不可能重合，所以这题我们需要初始化dp[i][i] = 1, 根据定义单个的就是1, 当然了如果我们在代码里特判一下也行，那样的话j就可以从i开始遍历

其余的我们就初始化为0就行

4.遍历顺序以及解的位置

遍历顺序我们i倒序， j从i+1开始，正序遍历
解的位置就是dp[0][n], 从头到尾序列中最长回文序列是多长

class Solution:
    def longestPalindromeSubseq(self, s: str) -> int:
        n = len(s)
        dp = [[0] * n for _ in range(n)]
        for i in range(n):
            dp[i][i] = 1
        
        for i in range(n-1, -1, -1):
            for j in range(i+1, n):
                if s[i] == s[j]:
                    dp[i][j] = dp[i+1][j-1] + 2
                else:
                    dp[i][j] = max(dp[i+1][j], dp[i][j-1])
        return dp[0][n-1]

代码随想录中动态规划总结

文章链接