一、简介

人工神经网络（Artificial Neural Network，即ANN ），是20世纪80 年代以来人工智能领域兴起的研究热点。它从信息处理角度对人脑神经元网络进行抽象， 建立某种简单模型，按不同的连接方式组成不同的网络。在工程与学术界也常直接简称为神经网络或类神经网络。神经网络是一种运算模型，由大量的节点（或称神经元）之间相互联接构成。每个节点代表一种特定的输出函数，称为激励函数（activation function）。每两个节点间的连接都代表一个对于通过该连接信号的加权值，称之为权重，这相当于人工神经网络的记忆。网络的输出则依网络的连接方式，权重值和激励函数的不同而不同。而网络自身通常都是对自然界某种算法或者函数的逼近，也可能是对一种逻辑策略的表达。
最近十多年来，人工神经网络的研究工作不断深入，已经取得了很大的进展，其在模式识别、智能机器人、自动控制、预测估计、生物、医学、经济等领域已成功地解决了许多现代计算机难以解决的实际问题，表现出了良好的智能特性。

二、ANN算法细节详解

2.1 深度学习要解决的问题

机器学习流程：

1. 数据获取
2. 特征工程
3. 建立模型
4. 评估与应用
5. 特征工程的作用：
   1.数据特征决定了模型的上限
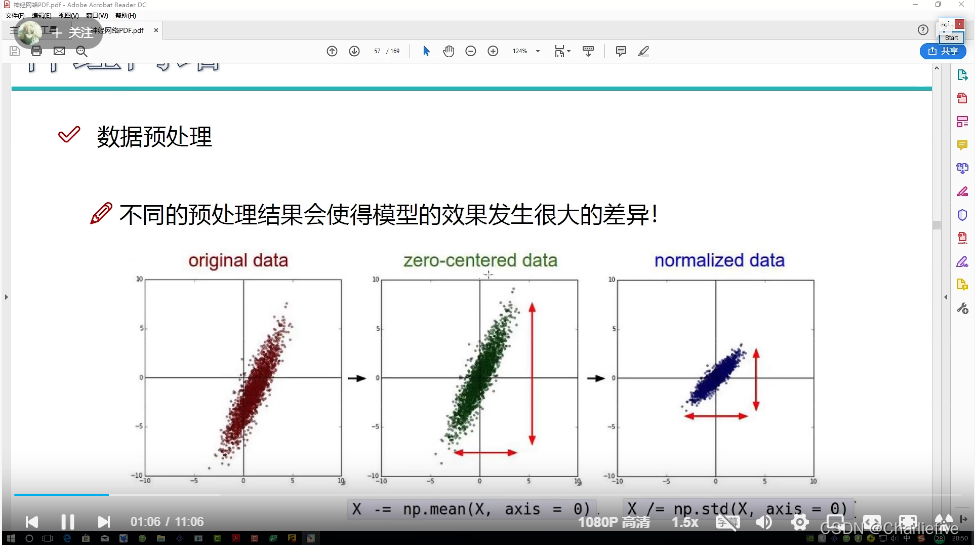
   2.预处理和特征提取是最核心的
   3.算法与参数决定了如何逼近这个上限

2.2 深度学习应用领域

很多

2.3 计算机视觉任务

计算机视觉：
图像分类任务
图像表示：计算机眼中的图像
一张图片被表示成三维数组的形式，每个像素的值从0到255。
像素点比如：8006003

计算机视觉面临的挑战：
1.照射角度
2.形状改变

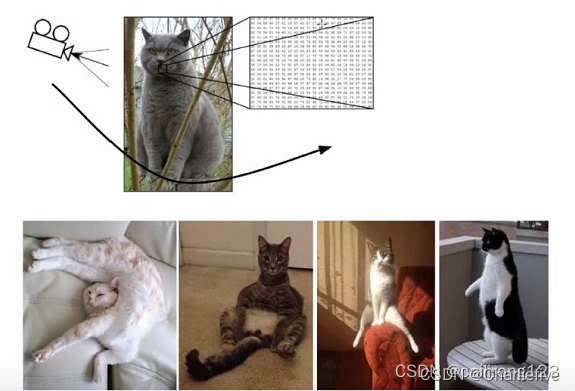
计算机视觉面临的挑战：
1.部分遮蔽
2.背景混入

2.4 视觉任务中遇到的问题

机器学习常规套路：

1. 收集数据并给定标签
2. 训练一个分类器
3. 测试，评估

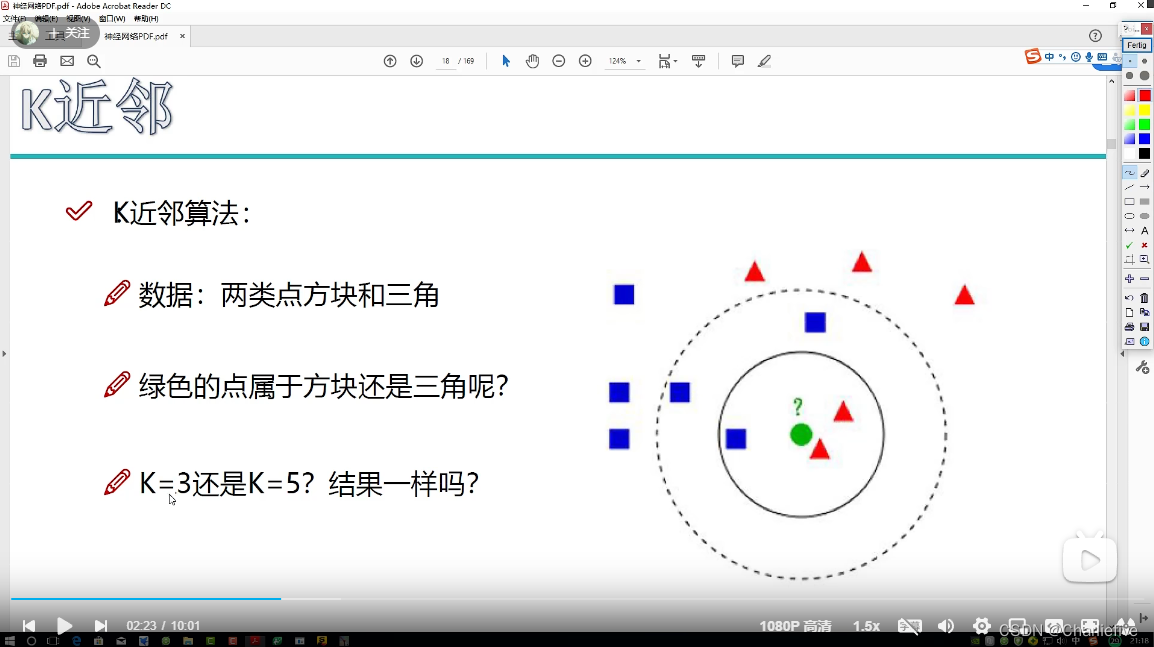
2.4.1回顾K近邻算法

当在K值不同时，界限的范围也不同，范围内每种元素的比例也不同，因此分类预测的结果也不相同，具体K近邻可以回顾以往的文章。

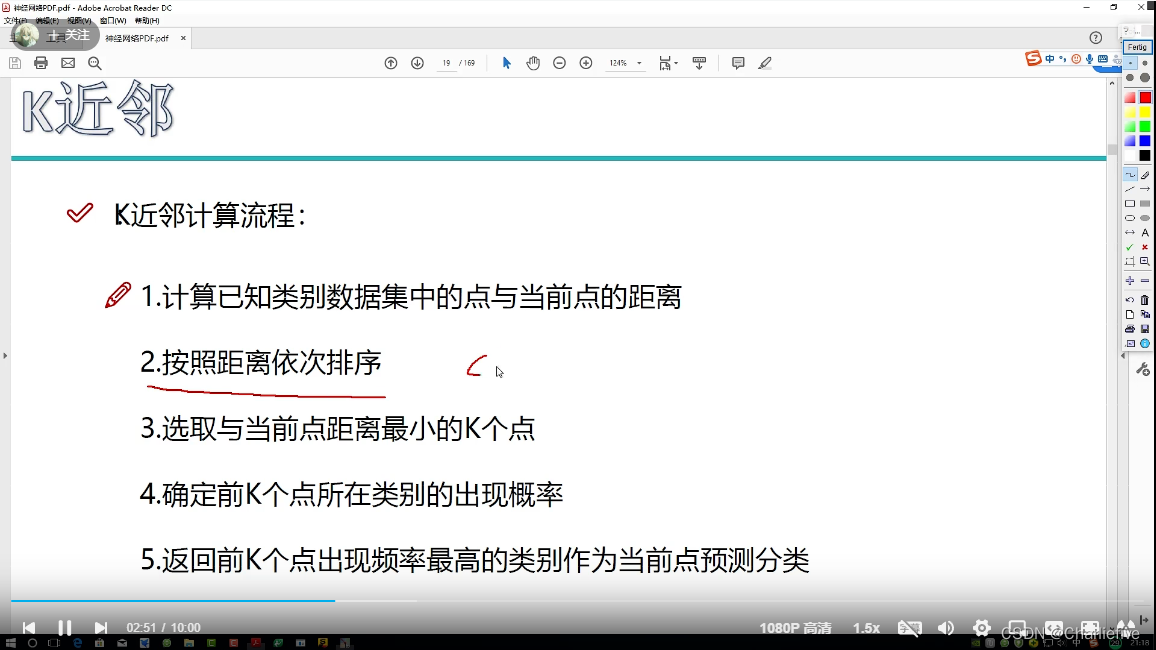
K近邻计算流程：
1.计算已知类别数据集中的点与当前点的距离
2.按照距离依次排序
3.选取与当前点距离最小的K个点
4.确定前k个点所在类别的出现概率
5.返回前K个点出现频率最高的类别作为当前预测分类
K近邻分析：
1.KNN算法本身简单有效，它是一种lazy–learning算法。
2.分类器不需要使用训练集进行训练，训练时间复杂度为0.
3.KNN分类的计算复杂度和训练集中的文档数目成正比，也就是说，如果训练集中文档总数为n，那么KNN的分类时间复杂度为O(n).
4.K值的选择，距离度量和分类决策规则是该算法的三个基本要素。
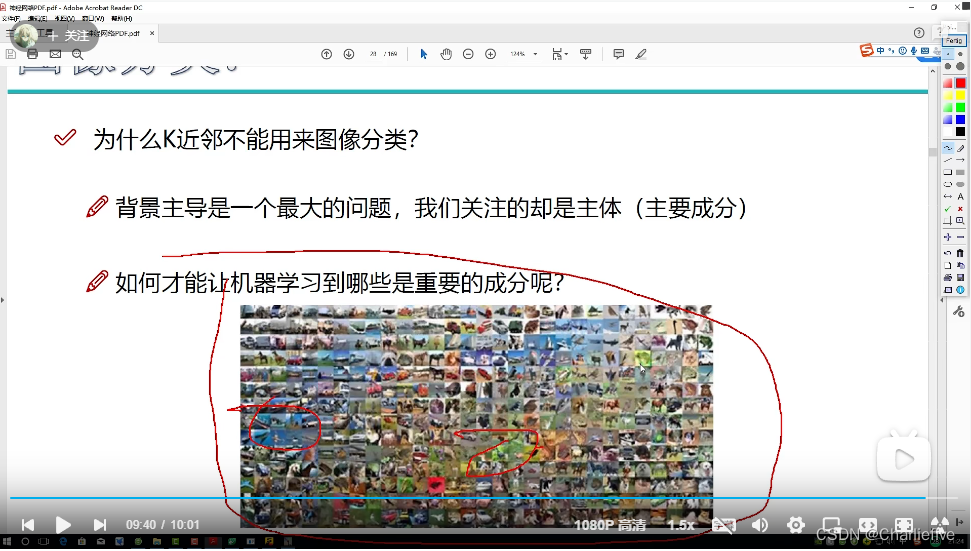
为什么k近邻不能用来图像分类？
背景主导是一个最大的问题，我们关注的却是主体（主要成分）
如何才能然机器学习到哪些是重要的成分呢？

2.4.2为啥不能用K近邻

我们识别图像，主要是根据主题内容，但是图像中的背景往往占据了更大的面积，即更大更多的像素点，使用K近邻会收到严重精确度的影响。

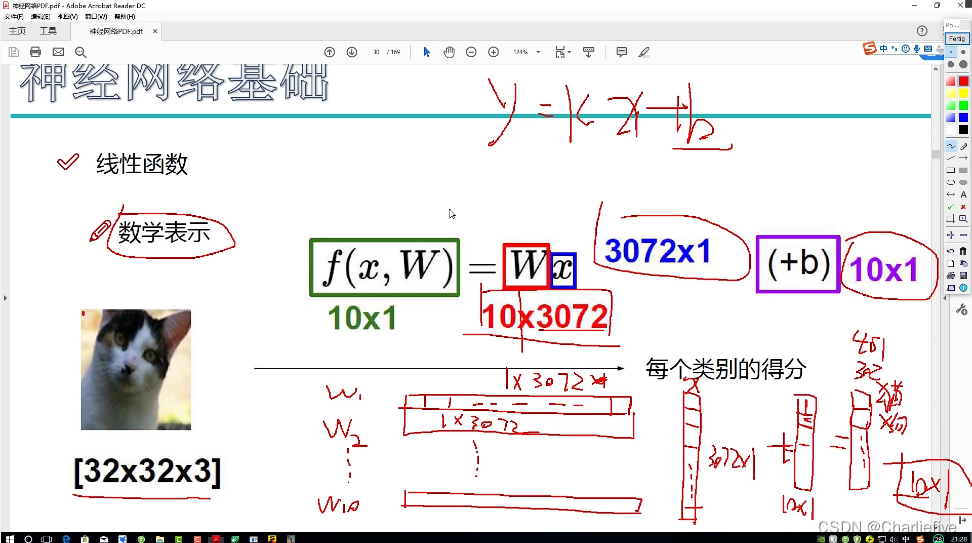
2.5得分函数

我们要算出一张图针对每一个类别的得分，以本图为例子有3072个像素点。W就是权重参数（每个类别都有一组参数点103072），x就是像素点（30721）。b是相当于对每个类别进行的微调。

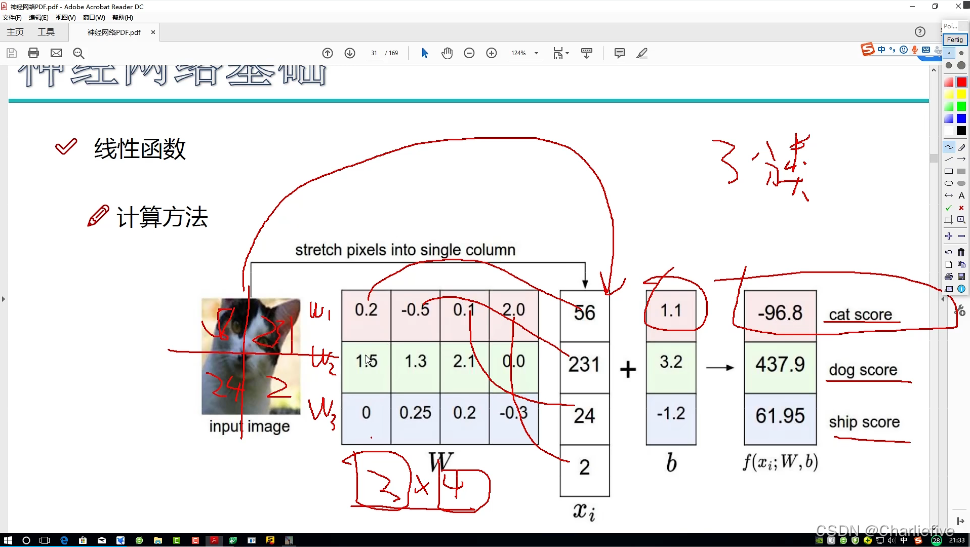
这种图更加形象说明了像素点以及分类特征之间的关系。将这种关系巧妙转化为数学公式关系。

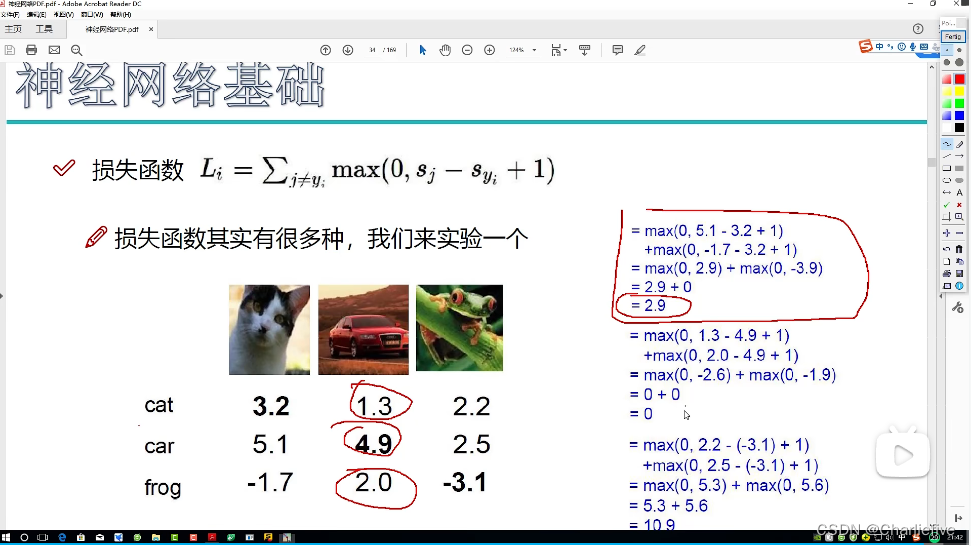
2.6损失函数

是一种关系计算损失的公式技巧，根据图中公式容易理解。
至于为什么在里边要+1，至少要有相差为1 的效果才能说明损失的程度较小。
损失函数计算数值越大，越不精确，误差更大。

加入一个正则化惩罚项，防止过度拟合。

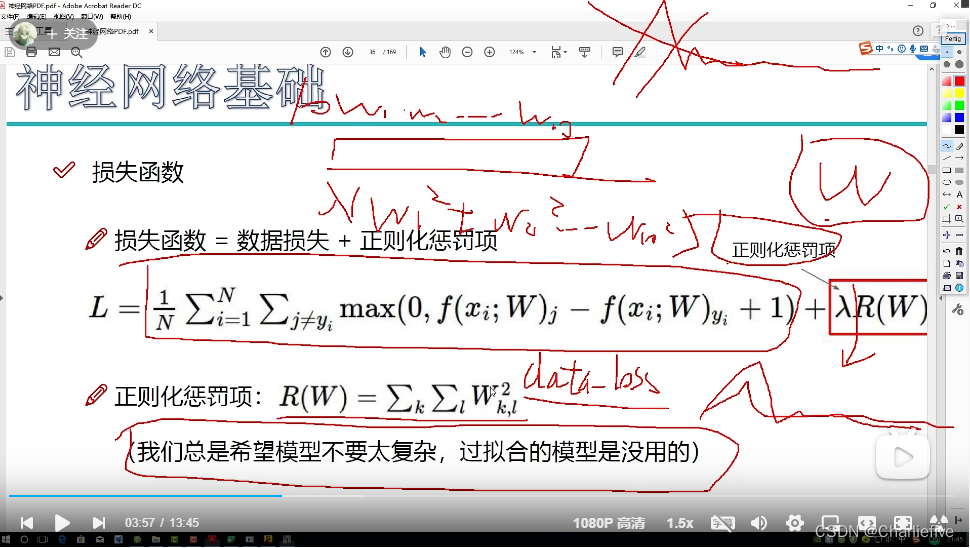
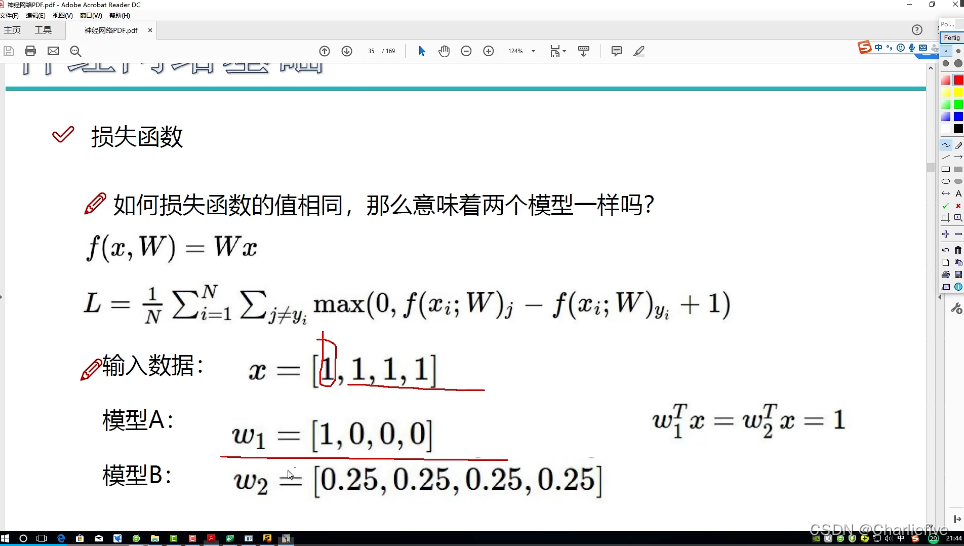
但是一种特殊情况，仅仅依靠损失函数的值判定是不准确的。比如一下情况

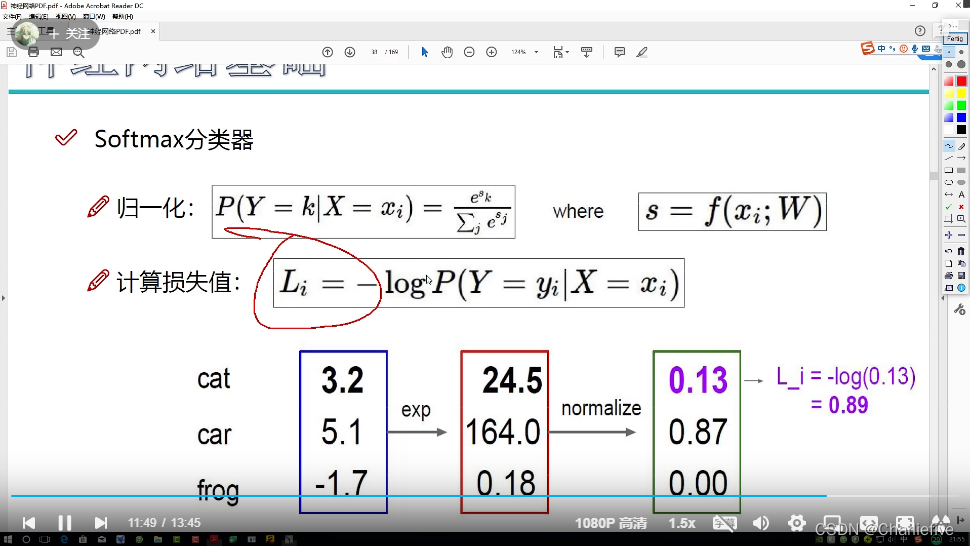
介绍Softmax分类器，这是计算损失值的正确打开方式。

2.7前向传播流程

正向传播是为了计算损失函数：

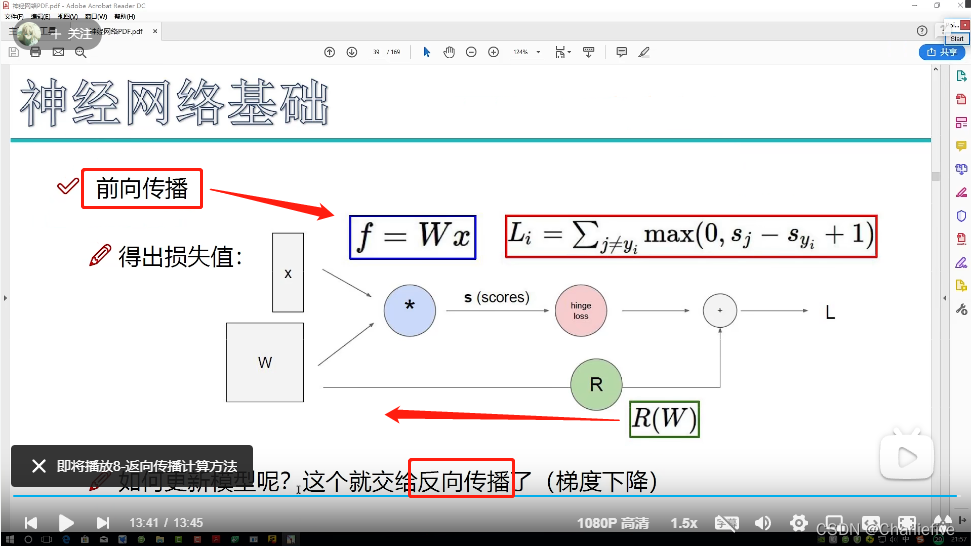
反向传播是为了更新模型、即系数参数:

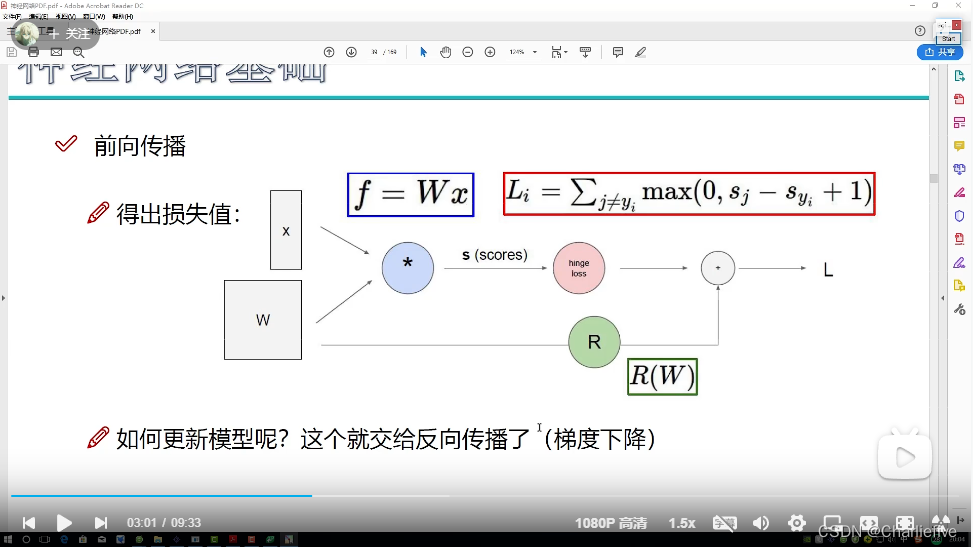
正向传播是一层一层加参数矩阵的过程
反向传播是求偏导更新的过程

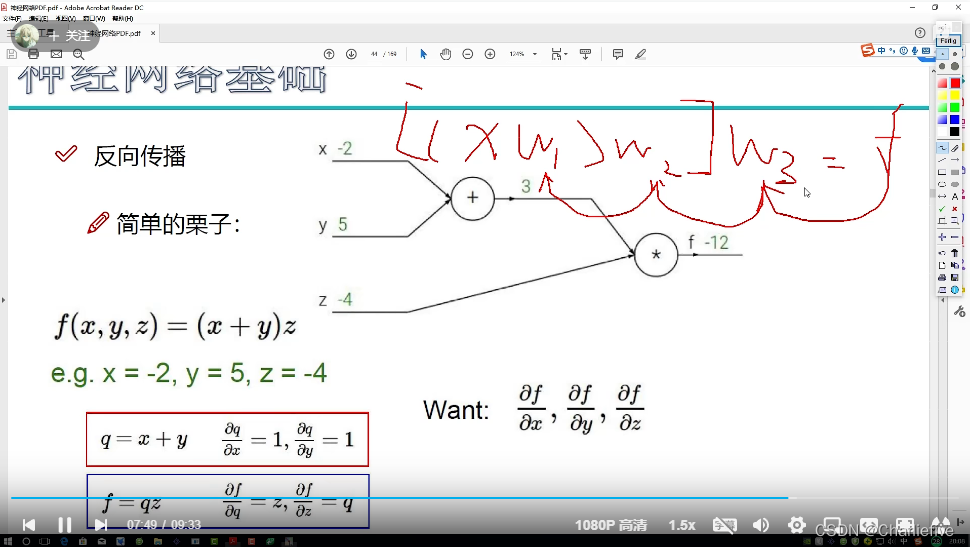
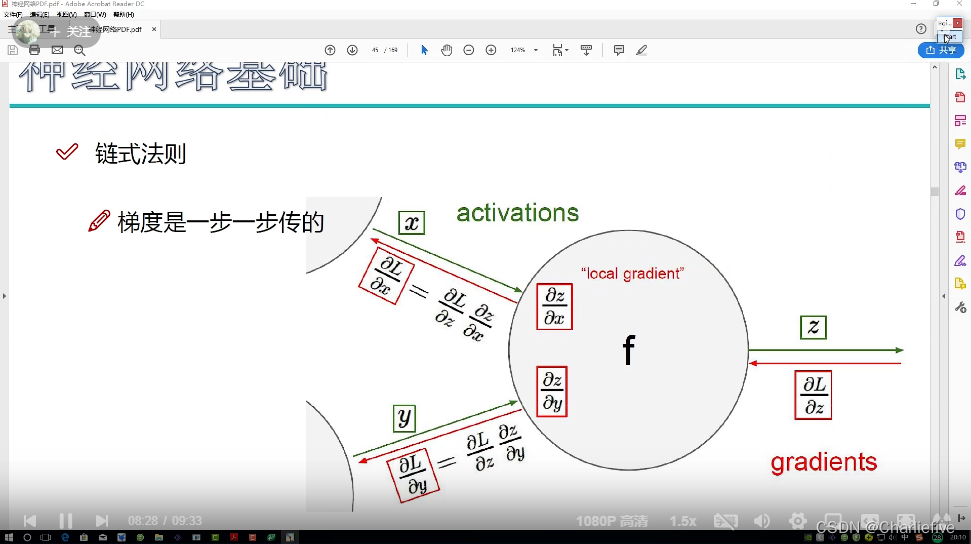
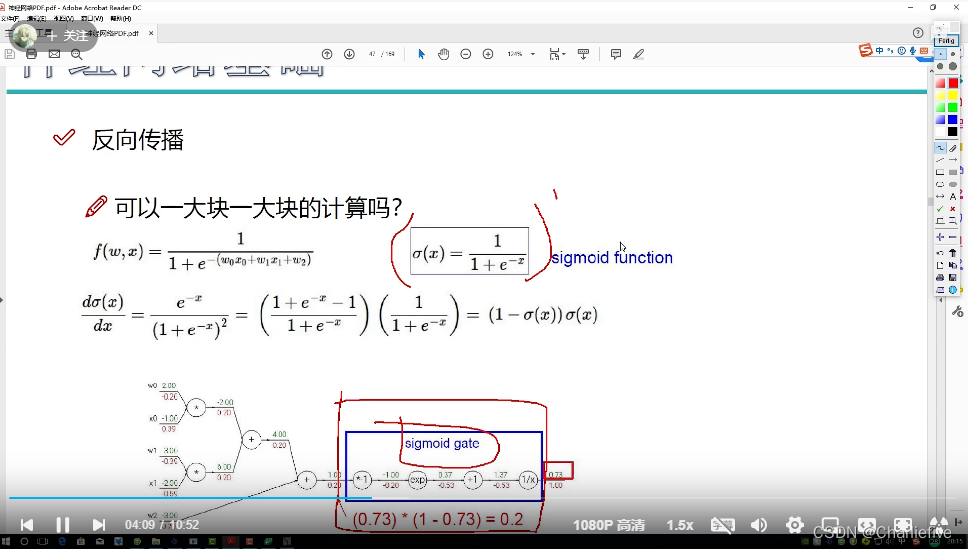
2.8反向传播计算

理解这个例子中反向传播的思想：
图中红字已经给出了过程了

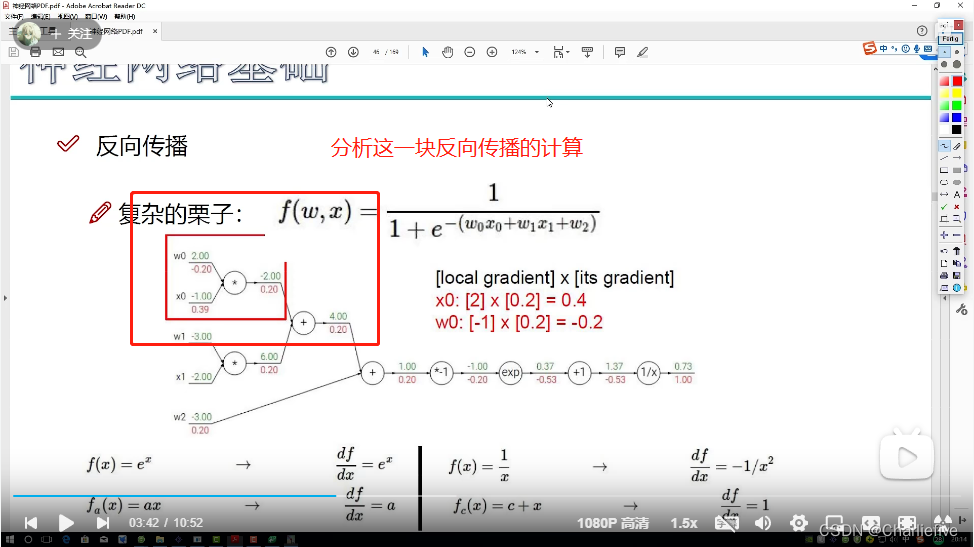
当然也可以一块一块算，一部分当成一块整体进行求偏导，都差不多无所谓的

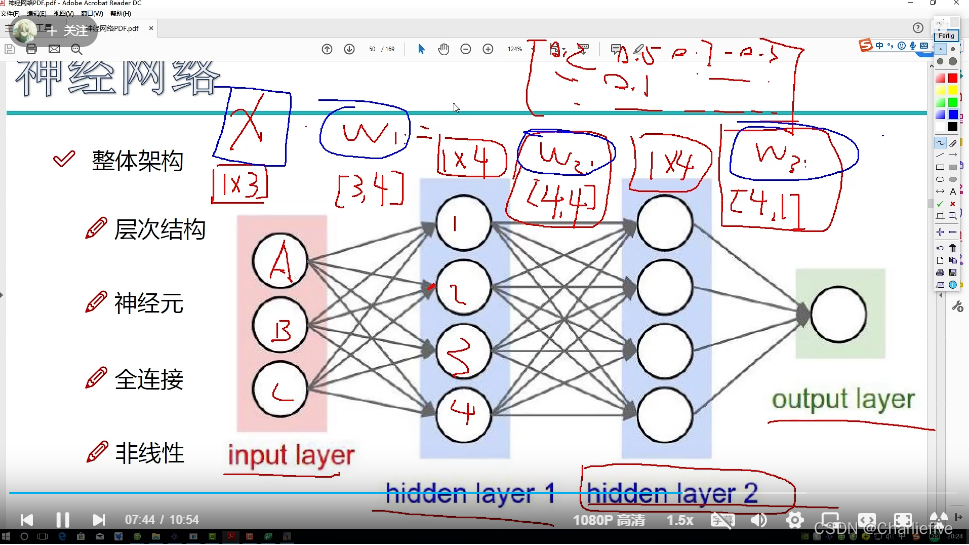
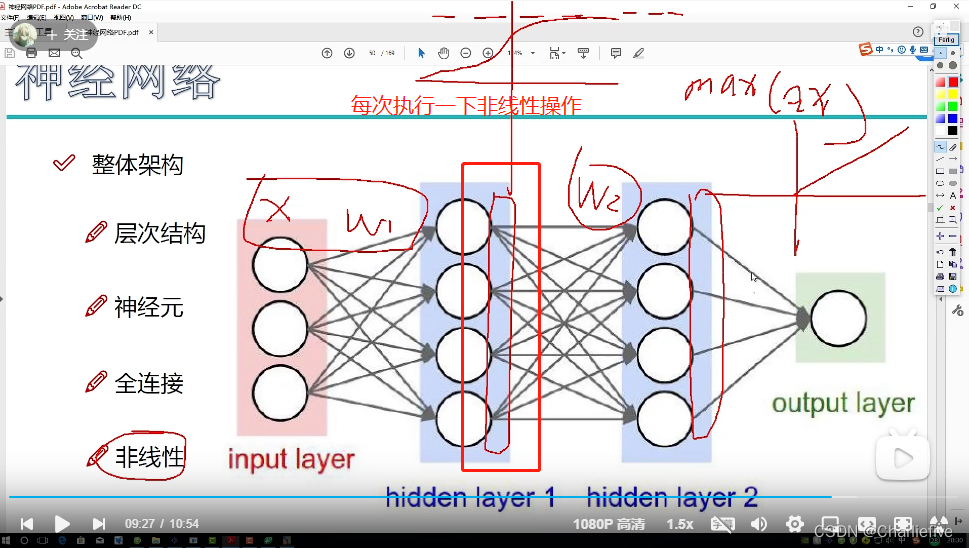
2.9神经网络整体架构

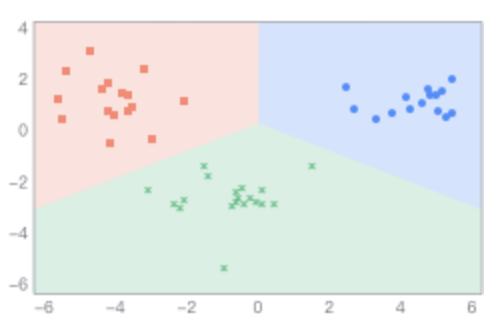
2.10神经元个数对结果的影响

可视化展示的神经网络https://cs.stanford.edu/people/karpathy/convnetjs/demo/classify2d.html

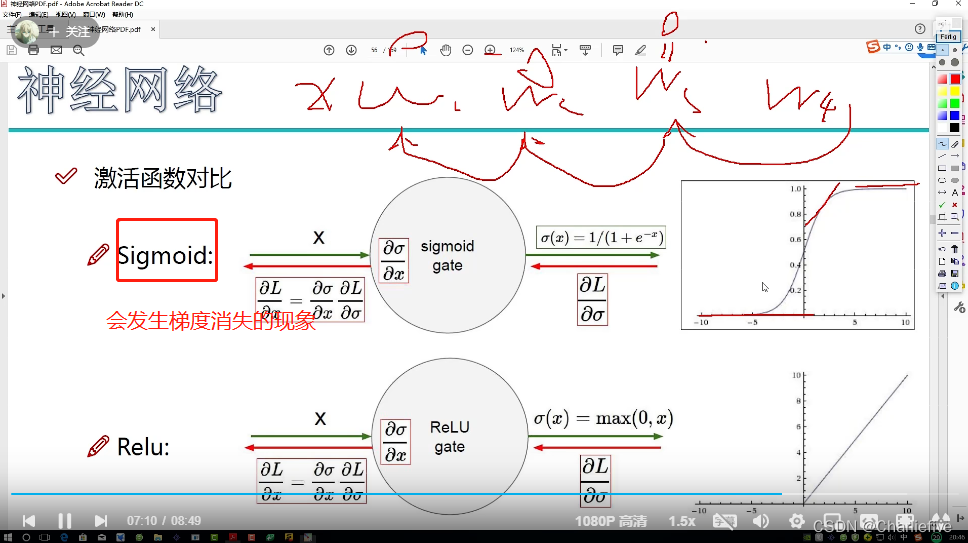
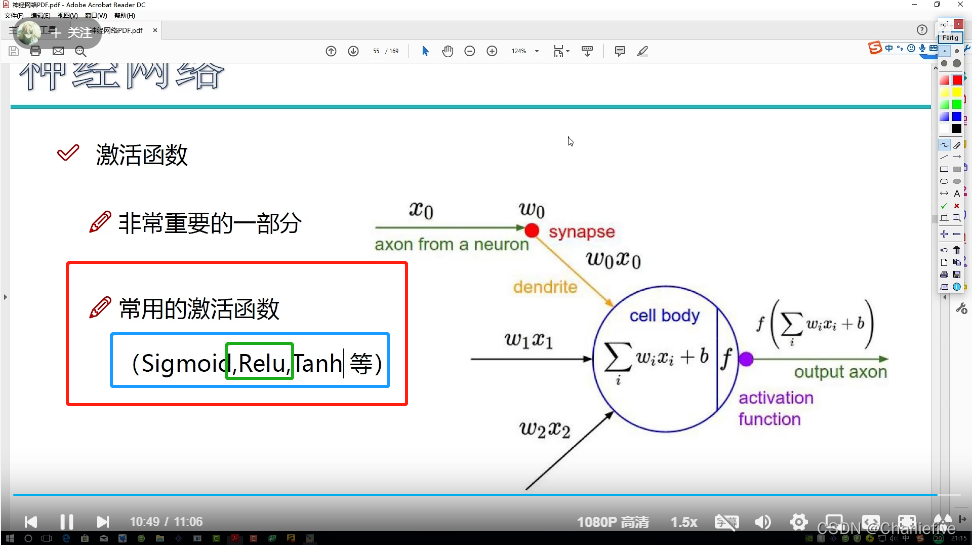
2.11正则化和激活函数

REUL。

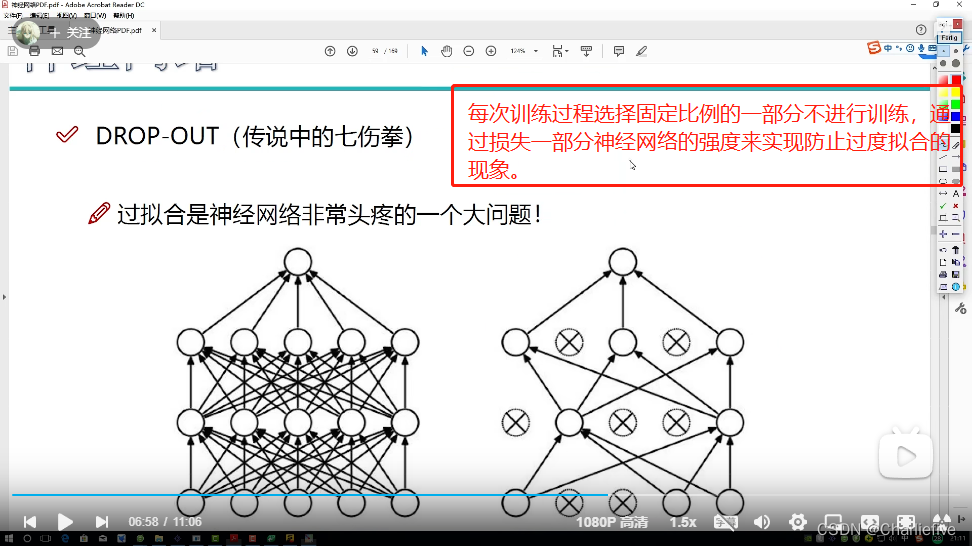
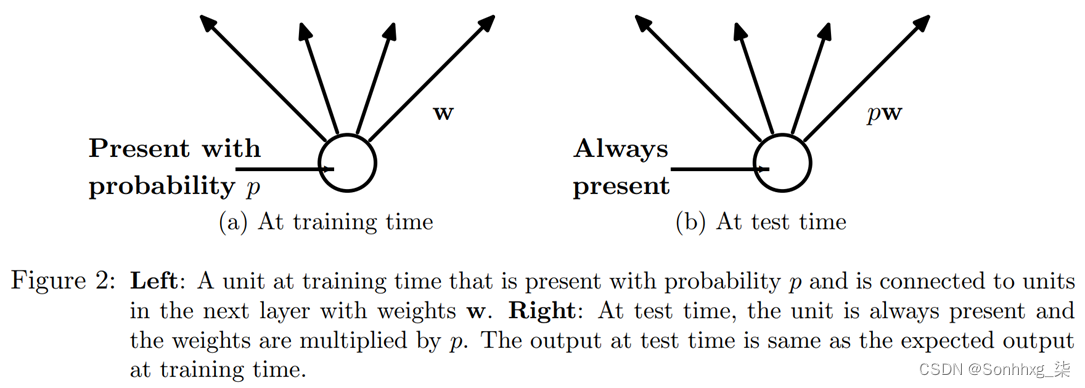
2.12过拟合解决