🔎大家好,我是Sonhhxg_柒,希望你看完之后,能对你有所帮助,不足请指正!共同学习交流🔎
📝个人主页-Sonhhxg_柒的博客_CSDN博客 📃
🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝
📣系列专栏 - 机器学习【ML】 自然语言处理【NLP】 深度学习【DL】
🖍foreword
✔说明⇢本人讲解主要包括Python、机器学习(ML)、深度学习(DL)、自然语言处理(NLP)等内容。
如果你对这个系列感兴趣的话,可以关注订阅哟👋
文章目录
数据
我们从零开始的第一个语言模型
我们在 PyTorch 中的语言模型
我们的第一个循环神经网络
改进循环神经网络
维护 RNN 的状态
创建更多信号
多层循环神经网络
该模型
爆炸或消失的激活
长短期记忆网络
从头开始构建 LSTM
使用 LSTM 训练语言模型
正则化 LSTM
Dropout
激活正则化和时间激活正则化
训练权重绑定正则化 LSTM
结论
我们现在准备深入……深入深度学习!你已经学会了如何训练一个基本的神经网络,但是你如何从那里开始创建最先进的模型呢?在本书的这一部分,我们将从语言模型开始揭开所有的谜团。
您在第 10 章中看到了如何微调预训练语言模型以构建文本分类器。在本章中,我们将准确解释该模型内部的内容以及 RNN 是什么。首先,让我们收集一些数据,以便我们快速制作各种模型的原型。
数据
每当我们开始处理一个新问题时,我们总是首先尝试考虑我们能想到的最简单的数据集,这将使我们能够快速轻松地尝试方法并解释结果。当我们开始工作 几年前在语言建模方面,我们没有找到任何可以快速制作原型的数据集,所以我们做了一个。我们称之为Human Numbers,它仅包含用英语写出的前 10,000 个数字。
即使在经验丰富的从业者中,我也看到最常见的实践错误之一是未能在分析过程中的适当时间使用适当的数据集。特别是,大多数人倾向于从太大和太复杂的数据集开始。
我们可以按照通常的方式下载、提取和查看我们的数据集:
from fastai.text.all import *
path = untar_data(URLs.HUMAN_NUMBERS)path.ls()(#2) [Path('train.txt'),Path('valid.txt')]
让我们打开这两个文件,看看里面有什么。首先,我们将所有文本连接在一起并忽略数据集给出的训练/有效分割(我们稍后会回过头来):
lines = L()
with open(path/'train.txt') as f: lines += L(*f.readlines())
with open(path/'valid.txt') as f: lines += L(*f.readlines())
lines(#9998) ['one \n','two \n','three \n','four \n','five \n','six \n','seven > \n','eight \n','nine \n','ten \n'...]
我们采用所有这些线并将它们连接成一个大流。为了标记我们何时从一个数字转到下一个数字,我们使用 a .作为分隔符:
text = ' . '.join([l.strip() for l in lines])
text[:100]'one . two . three . four . five . six . seven . eight . nine . ten . eleven . > twelve . thirteen . fo'
我们可以通过按空格拆分来标记此数据集:
tokens = text.split(' ')
tokens[:10]['one', '.', 'two', '.', 'three', '.', 'four', '.', 'five', '.']
要进行数字化,我们必须创建一个包含所有唯一标记(我们的 词汇)的列表:
vocab = L(*tokens).unique()
vocab(#30) ['one','.','two','three','four','five','six','seven','eight','nine'...]
然后我们可以通过查找词汇表中每个标记的索引将标记转换为数字:
word2idx = {w:i for i,w in enumerate(vocab)}
nums = L(word2idx[i] for i in tokens)
nums(#63095) [0,1,2,1,3,1,4,1,5,1...]
我们从零开始的第一个语言模型
将其转换为神经网络的一种简单方法是指定我们将根据前三个词预测每个词。我们可以创建一个包含三个序列的列表 单词作为我们的自变量,每个序列之后的下一个单词作为因变量。
我们可以用普通的 Python 来做到这一点。让我们先用令牌来做,只是为了确认它是什么样子的:
L((tokens[i:i+3], tokens[i+3]) for i in range(0,len(tokens)-4,3))(#21031) [(['one', '.', 'two'], '.'),(['.', 'three', '.'], 'four'),(['four', > '.', 'five'], '.'),(['.', 'six', '.'], 'seven'),(['seven', '.', 'eight'], > '.'),(['.', 'nine', '.'], 'ten'),(['ten', '.', 'eleven'], '.'),(['.', > 'twelve', '.'], 'thirteen'),(['thirteen', '.', 'fourteen'], '.'),(['.', > 'fifteen', '.'], 'sixteen')...]
现在我们将使用数值张量来完成,这是模型实际使用的:
seqs = L((tensor(nums[i:i+3]), nums[i+3]) for i in range(0,len(nums)-4,3))
seqs(#21031) [(tensor([0, 1, 2]), 1),(tensor([1, 3, 1]), 4),(tensor([4, 1, 5]), > 1),(tensor([1, 6, 1]), 7),(tensor([7, 1, 8]), 1),(tensor([1, 9, 1]), > 10),(tensor([10, 1, 11]), 1),(tensor([ 1, 12, 1]), 13),(tensor([13, 1, > 14]), 1),(tensor([ 1, 15, 1]), 16)...]
我们可以使用DataLoader该类轻松地对这些进行批处理。现在,我们将随机拆分序列:
bs = 64
cut = int(len(seqs) * 0.8)
dls = DataLoaders.from_dsets(seqs[:cut], seqs[cut:], bs=64, shuffle=False)我们现在可以创建一个神经网络架构,它将三个词作为输入,并返回对词汇中每个可能的下一个词的概率的预测。我们将使用三个标准线性层,但有两个调整。
第一个调整是第一个线性层将仅使用第一个词的嵌入作为激活,第二层将使用第二个词的嵌入加上第一层的输出激活,第三层将使用第三个词的嵌入加上第二层的输出激活。关键效果是每个单词都在其前面的任何单词的信息上下文中进行解释。
第二个调整是这三层中的每一层都将使用相同的权重矩阵。一个词影响前一个词的激活的方式不应该根据一个词的位置而改变。换句话说,激活值会随着数据在层中移动而改变,但层权重本身不会在层与层之间发生变化。所以,一层不学习一个序列位置;它必须学会处理所有位置。
由于层权重不会改变,您可能会将顺序层视为重复的“同一层”。事实上,PyTorch 使这一点变得具体;我们可以只创建一层并多次使用它。
我们在 PyTorch 中的语言模型
class LMModel1(Module):
def __init__(self, vocab_sz, n_hidden):
self.i_h = nn.Embedding(vocab_sz, n_hidden)
self.h_h = nn.Linear(n_hidden, n_hidden)
self.h_o = nn.Linear(n_hidden,vocab_sz)
def forward(self, x):
h = F.relu(self.h_h(self.i_h(x[:,0])))
h = h + self.i_h(x[:,1])
h = F.relu(self.h_h(h))
h = h + self.i_h(x[:,2])
h = F.relu(self.h_h(h))
return self.h_o(h)如您所见,我们创建了三层:
-
嵌入层(
i_h,用于隐藏的输入) -
为下一个词创建激活的线性层(
h_h,隐藏到隐藏) -
预测第四个词的最终线性层(
h_o,隐藏到输出)
这可能更容易以图形形式表示,所以让我们定义基本神经网络的简单图形表示。 图 12-1显示了我们将如何表示具有一个隐藏层的神经网络。

图 12-1。简单神经网络的图示
每个形状代表激活:矩形用于输入,圆形用于隐藏(内)层激活,三角形用于输出激活。我们将在本章的所有图表中使用这些形状(在图 12-2中进行了总结)。

图 12-2。我们的图示中使用的形状
箭头表示实际的层计算——即线性层后跟激活函数。使用这种表示法, 图 12-3显示了我们的简单语言模型的样子。
图 12-3。我们的基本语言模型的表示
为了简化事情,我们从每个箭头中删除了层计算的细节。我们还对箭头进行了颜色编码,这样所有具有相同颜色的箭头都具有相同的权重矩阵。例如,所有输入层都使用相同的嵌入矩阵,因此它们都具有相同的颜色(绿色)。
learn = Learner(dls, LMModel1(len(vocab), 64), loss_func=F.cross_entropy,
metrics=accuracy)
learn.fit_one_cycle(4, 1e-3)| epoch | train_loss | vaild_loss | accuracy | time |
|---|---|---|---|---|
| 0 | 1.824297 | 1.970941 | 0.467554 | 00:02 |
| 1 | 1.386973 | 1.823242 | 0.467554 | 00:02 |
| 2 | 1.417556 | 1.654497 | 0.494414 | 00:02 |
| 3 | 1.376440 | 1.650849 | 0.494414 | 00:02 |
要查看这是否有任何好处,让我们检查一个非常简单的模型会给我们带来什么。在这种情况下,我们总是可以预测最 通用标记,所以让我们找出哪个标记最常成为我们验证集中的目标:
n,counts = 0,torch.zeros(len(vocab))
for x,y in dls.valid:
n += y.shape[0]
for i in range_of(vocab): counts[i] += (y==i).long().sum()
idx = torch.argmax(counts)
idx, vocab[idx.item()], counts[idx].item()/n(tensor(29), 'thousand', 0.15165200855716662)
最常见的令牌具有索引 29,对应于令牌 thousand。始终预测这个标记会给我们大约 15% 的准确度,所以我们的表现要好得多!
我的第一个猜测是分隔符将是最常见的标记,因为每个数字都有一个分隔符。但是看着
tokens提醒我,大数字是用很多字写的,所以在到 10,000 的路上你写了很多“千”:五千,五千零一,五千零二,等等。哎呀!查看您的数据非常适合注意到细微的特征以及令人尴尬的明显特征。
这是一个很好的第一个基线。让我们看看如何用循环重构它。
我们的第一个循环神经网络
查看我们模块的代码,我们可以通过用for循环替换调用层的重复代码来简化它。除了使我们的代码更简单之外,这还有一个好处,我们将能够 将我们的模块同样适用于不同长度的标记序列——我们不会局限于长度为三的标记列表:
class LMModel2(Module):
def __init__(self, vocab_sz, n_hidden):
self.i_h = nn.Embedding(vocab_sz, n_hidden)
self.h_h = nn.Linear(n_hidden, n_hidden)
self.h_o = nn.Linear(n_hidden,vocab_sz)
def forward(self, x):
h = 0
for i in range(3):
h = h + self.i_h(x[:,i])
h = F.relu(self.h_h(h))
return self.h_o(h)让我们检查使用此重构是否得到相同的结果:
learn = Learner(dls, LMModel2(len(vocab), 64), loss_func=F.cross_entropy,
metrics=accuracy)
learn.fit_one_cycle(4, 1e-3)| epoch | train_loss | vaild_loss | accuracy | time |
|---|---|---|---|---|
| 0 | 1.816274 | 1.964143 | 0.460185 | 00:02 |
| 1 | 1.423805 | 1.739964 | 0.473259 | 00:02 |
| 2 | 1.430327 | 1.685172 | 0.485382 | 00:02 |
| 3 | 1.388390 | 1.657033 | 0.470406 | 00:02 |
我们也可以用完全相同的方式重构我们的图形表示,如图 12-4所示(我们在这里也删除了激活大小的细节,并使用与 图 12-3中相同的箭头颜色)。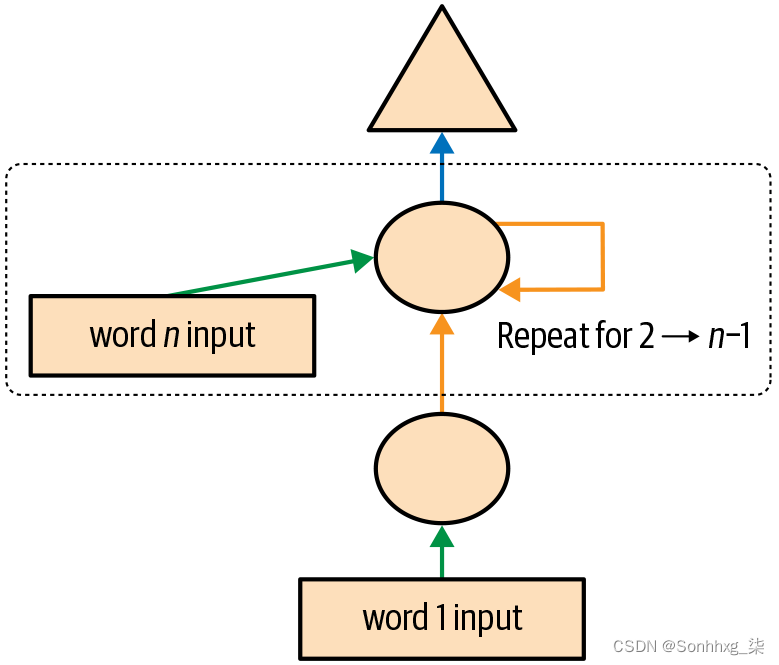
图 12-4。基本循环神经网络
你会看到每次循环都会更新一组激活,存储在变量中h——这是 称为隐藏状态。
隐藏状态
在递归神经网络的每一步更新的激活。
使用这样的循环定义的神经网络称为 递归神经网络(RNN)。重要的是要 意识到 RNN 不是一个复杂的新架构,而只是使用for循环对多层神经网络的重构。
我的真实观点:如果将它们称为“循环神经网络”或 LNN,它们看起来会不那么令人生畏 50%!
现在我们知道什么是 RNN,让我们试着让它变得更好一点。
改进循环神经网络
查看我们的 RNN 代码,似乎有问题的一件事是 我们正在为每个新的输入序列将隐藏状态初始化为零。为什么这是个问题?我们缩短了样本序列,以便它们可以轻松放入批次中。但是,如果我们正确地对这些样本进行排序,模型将按顺序读取样本序列,从而将模型暴露于原始序列的很长一段。
我们可以看到的另一件事是有更多的信号:当我们可以使用中间预测来预测第二个和第三个单词时,为什么只预测第四个单词?让我们看看如何实现这些更改,从添加一些状态开始。
维护 RNN 的状态
因为我们为每个新样本将模型的隐藏状态初始化为零,所以我们丢弃了所有关于 到目前为止我们看到的句子,这意味着我们的模型实际上并不知道我们在整个计数序列中的位置。这很容易修复;我们可以简单地将隐藏状态的初始化移动到__init__。
但是这个修复会产生它自己的微妙但重要的问题。它有效地使我们的神经网络与文档中的标记总数一样深。例如,如果我们的数据集中有 10,000 个标记,我们将创建一个 10,000 层的神经网络。
要了解为什么会这样,请考虑图 12-3for中循环神经网络的原始图形表示,然后再使用循环对其进行重构。您可以看到每一层对应一个令牌输入。当我们在用循环重构之前谈论循环神经网络的表示时for,我们称之为展开表示。在尝试理解 RNN 时考虑展开表示通常很有帮助。
10,000 层神经网络的问题在于,如果当你到达数据集的第 10,000 个单词时,你仍然需要计算导数一直回到第一层。这确实会很慢,而且会占用大量内存。您不太可能能够在 GPU 上存储一个小批量。
这个问题的解决方案是告诉 PyTorch 我们不想通过整个隐式神经网络反向传播导数。相反,我们将只保留最后三层渐变。要删除 PyTorch 中的所有梯度历史记录,我们使用该detach方法。
这是我们 RNN 的新版本。它现在是有状态的,因为它会记住它在对 的不同调用之间的激活forward,这代表它对批处理中不同样本的使用:
class LMModel3(Module):
def __init__(self, vocab_sz, n_hidden):
self.i_h = nn.Embedding(vocab_sz, n_hidden)
self.h_h = nn.Linear(n_hidden, n_hidden)
self.h_o = nn.Linear(n_hidden,vocab_sz)
self.h = 0
def forward(self, x):
for i in range(3):
self.h = self.h + self.i_h(x[:,i])
self.h = F.relu(self.h_h(self.h))
out = self.h_o(self.h)
self.h = self.h.detach()
return out
def reset(self): self.h = 0无论我们选择什么序列长度,这个模型都会有相同的激活,因为隐藏状态会记住上一批次的最后一次激活。唯一不同的是在每一步计算的梯度:它们将只根据过去的序列长度标记计算,而不是整个流。这种方法称为时间反向传播(BPTT)。
时间反向传播
要使用LMModel3,我们需要确保样本将按特定顺序显示。正如我们在第 10 章中看到的,如果第一批的第一行是我们的dset[0],那么第二批的第一行应该是我们的dset[1],以便模型看到文本流动。
LMDataLoader在第 10 章中为我们做了这个。这次我们要 自己动手。
为此,我们将重新排列我们的数据集。首先,我们将样本分成 m = len(dset) // bs几组(这相当于将整个连接的数据集分成,例如,64 个大小相同的部分,因为我们在bs=64这里使用)。m是每个片段的长度。例如,如果我们正在使用我们的整个数据集(虽然我们实际上会将其分成训练集和有效集),我们有这个:
m = len(seqs)//bs
m,bs,len(seqs)(328, 64, 21031)
第一批将由样品组成
(0, m, 2*m, ..., (bs-1)*m)第二批样品
(1, m+1, 2*m+1, ..., (bs-1)*m+1)等等。这样,在每个时期,模型将3*m在批处理的每一行上看到一大块大小为 3 的连续文本(因为每个文本的大小为 3)。
以下函数执行重新索引:
def group_chunks(ds, bs):
m = len(ds) // bs
new_ds = L()
for i in range(m): new_ds += L(ds[i + m*j] for j in range(bs))
return new_ds然后我们drop_last=True在构建我们的时候就通过DataLoaders删除最后一批没有形状的bs。我们还传递 shuffle=False以确保按顺序阅读文本:
cut = int(len(seqs) * 0.8)
dls = DataLoaders.from_dsets(
group_chunks(seqs[:cut], bs),
group_chunks(seqs[cut:], bs),
bs=bs, drop_last=True, shuffle=False)我们添加的最后一件事是通过 Callback. 我们将更多地讨论回调 第16章;这个将reset在每个纪元开始和每个验证阶段之前调用我们模型的方法。由于我们实现了该方法以将模型的隐藏状态设置为零,这将确保我们在读取那些连续的文本块之前从一个干净的状态开始。我们还可以开始更长时间的训练:
learn = Learner(dls, LMModel3(len(vocab), 64), loss_func=F.cross_entropy,
metrics=accuracy, cbs=ModelResetter)
learn.fit_one_cycle(10, 3e-3)| epoch | train_loss | vaild_loss | accuracy | time |
|---|---|---|---|---|
| 0 | 1.677074 | 1.827367 | 0.467548 | 00:02 |
| 1 | 1.282722 | 1.870913 | 0.388942 | 00:02 |
| 2 | 1.090705 | 1.651793 | 0.462500 | 00:02 |
| 3 | 1.005092 | 1.613794 | 0.516587 | 00:02 |
| 4 | 0.965975 | 1.560775 | 0.551202 | 00:02 |
| 5 | 0.916182 | 1.595857 | 0.560577 | 00:02 |
| 6 | 0.897657 | 1.539733 | 0.574279 | 00:02 |
| 7 | 0.836274 | 1.585141 | 0.583173 | 00:02 |
| 8 | 0.805877 | 1.629808 | 0.586779 | 00:02 |
| 9 | 0.795096 | 1.651267 | 0.588942 | 00:02 |
这已经更好了!下一步是使用更多目标并将它们与中间预测进行比较。
创建更多信号
我们当前方法的另一个问题是,对于每三个输入词,我们只预测一个输出词。结果,数量 我们正在反馈以更新权重的信号并不像它应该的那么大。如果我们在每个单词之后而不是每三个单词之后预测下一个单词会更好, 如图 12-5所示。
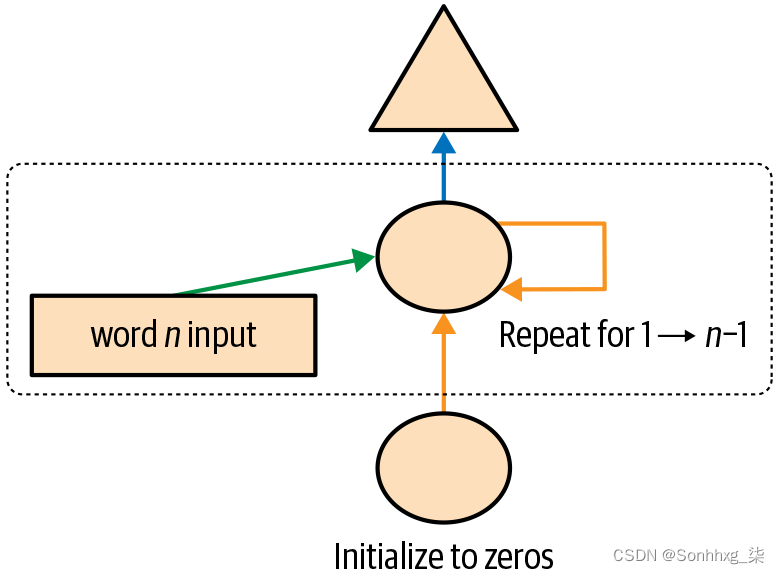
图 12-5。RNN 在每个标记后进行预测
这很容易添加。我们需要首先更改我们的数据,以便因变量在我们的三个输入词中的每一个之后都有接下来的三个词中的每一个。取而代之的是3,我们使用一个属性sl(用于序列长度),并使其更大一些:
sl = 16
seqs = L((tensor(nums[i:i+sl]), tensor(nums[i+1:i+sl+1]))
for i in range(0,len(nums)-sl-1,sl))
cut = int(len(seqs) * 0.8)
dls = DataLoaders.from_dsets(group_chunks(seqs[:cut], bs),
group_chunks(seqs[cut:], bs),
bs=bs, drop_last=True, shuffle=False)查看 的第一个元素seqs,我们可以看到它包含两个相同大小的列表。第二个列表与第一个列表相同,但偏移了一个元素:
[L(vocab[o] for o in s) for s in seqs[0]][(#16) ['one','.','two','.','three','.','four','.','five','.'...], (#16) ['.','two','.','three','.','four','.','five','.','six'...]]
现在我们需要修改我们的模型,让它在每个单词之后输出一个预测,而不是仅仅在三个单词序列的末尾:
class LMModel4(Module):
def __init__(self, vocab_sz, n_hidden):
self.i_h = nn.Embedding(vocab_sz, n_hidden)
self.h_h = nn.Linear(n_hidden, n_hidden)
self.h_o = nn.Linear(n_hidden,vocab_sz)
self.h = 0
def forward(self, x):
outs = []
for i in range(sl):
self.h = self.h + self.i_h(x[:,i])
self.h = F.relu(self.h_h(self.h))
outs.append(self.h_o(self.h))
self.h = self.h.detach()
return torch.stack(outs, dim=1)
def reset(self): self.h = 0该模型将返回形状的输出bs x sl x vocab_sz(因为我们堆叠在 上dim=1)。我们的目标是形状的bs x sl,所以我们需要在使用它们之前将它们展平F.cross_entropy:
def loss_func(inp, targ):
return F.cross_entropy(inp.view(-1, len(vocab)), targ.view(-1))我们现在可以使用这个损失函数来训练模型:
learn = Learner(dls, LMModel4(len(vocab), 64), loss_func=loss_func,
metrics=accuracy, cbs=ModelResetter)
learn.fit_one_cycle(15, 3e-3)| epoch | train_loss | vaild_loss | accuracy | time |
|---|---|---|---|---|
| 0 | 3.103298 | 2.874341 | 0.212565 | 00:01 |
| 1 | 2.231964 | 1.971280 | 0.462158 | 00:01 |
| 2 | 1.711358 | 1.813547 | 0.461182 | 00:01 |
| 3 | 1.448516 | 1.828176 | 0.483236 | 00:01 |
| 4 | 1.288630 | 1.659564 | 0.520671 | 00:01 |
| 5 | 1.161470 | 1.714023 | 0.554932 | 00:01 |
| 6 | 1.055568 | 1.660916 | 0.575033 | 00:01 |
| 7 | 0.960765 | 1.719624 | 0.591064 | 00:01 |
| 8 | 0.870153 | 1.839560 | 0.614665 | 00:01 |
| 9 | 0.808545 | 1.770278 | 0.624349 | 00:01 |
| 10 | 0.758084 | 1.842931 | 0.610758 | 00:01 |
| 11 | 0.719320 | 1.799527 | 0.646566 | 00:01 |
| 12 | 0.683439 | 1.917928 | 0.649821 | 00:01 |
| 13 | 0.660283 | 1.874712 | 0.628581 | 00:01 |
| 14 | 0.646154 | 1.877519 | 0.640055 | 00:01 |
我们需要训练更长时间,因为现在任务发生了一些变化并且更加复杂。但我们最终得到了一个好结果……至少,有时是这样。如果你运行它几次,你会发现在不同的运行中你会得到完全不同的结果。那是因为实际上我们这里有一个非常深的网络,这会导致非常大或非常小的梯度。我们将在本章的下一部分看到如何处理这个问题。
现在,获得更好模型的明显方法是更深入:我们在基本 RNN 中的隐藏状态和输出激活之间只有一个线性层,所以也许我们会得到更好的结果。
多层循环神经网络
在多层 RNN 中,我们将循环神经网络的激活传递给第二个循环神经网络,如 图 12-6。

图 12-6。2层循环神经网络
展开的表示如图 12-7所示(类似于图 12-3)。

图 12-7。2 层展开的 RNN
让我们看看如何在实践中实现这一点。
该模型
我们可以通过使用 PyTorch 的RNN 类来节省一些时间,它完全实现了我们之前创建的内容,但也为我们提供了堆叠多个 RNN 的选项,正如我们所讨论的:
class LMModel5(Module):
def __init__(self, vocab_sz, n_hidden, n_layers):
self.i_h = nn.Embedding(vocab_sz, n_hidden)
self.rnn = nn.RNN(n_hidden, n_hidden, n_layers, batch_first=True)
self.h_o = nn.Linear(n_hidden, vocab_sz)
self.h = torch.zeros(n_layers, bs, n_hidden)
def forward(self, x):
res,h = self.rnn(self.i_h(x), self.h)
self.h = h.detach()
return self.h_o(res)
def reset(self): self.h.zero_()learn = Learner(dls, LMModel5(len(vocab), 64, 2),
loss_func=CrossEntropyLossFlat(),
metrics=accuracy, cbs=ModelResetter)
learn.fit_one_cycle(15, 3e-3)| epoch | train_loss | vaild_loss | accuracy | time |
|---|---|---|---|---|
| 0 | 3.055853 | 2.591640 | 0.437907 | 00:01 |
| 1 | 2.162359 | 1.787310 | 0.471598 | 00:01 |
| 2 | 1.710663 | 1.941807 | 0.321777 | 00:01 |
| 3 | 1.520783 | 1.999726 | 0.312012 | 00:01 |
| 4 | 1.330846 | 2.012902 | 0.413249 | 00:01 |
| 5 | 1.163297 | 1.896192 | 0.450684 | 00:01 |
| 6 | 1.033813 | 2.005209 | 0.434814 | 00:01 |
| 7 | 0.919090 | 2.047083 | 0.456706 | 00:01 |
| 8 | 0.822939 | 2.068031 | 0.468831 | 00:01 |
| 9 | 0.750180 | 2.136064 | 0.475098 | 00:01 |
| 10 | 0.695120 | 2.139140 | 0.485433 | 00:01 |
| 11 | 0.655752 | 2.155081 | 0.493652 | 00:01 |
| 12 | 0.629650 | 2.162583 | 0.498535 | 00:01 |
| 13 | 0.613583 | 2.171649 | 0.491048 | 00:01 |
| 14 | 0.604309 | 2.180355 | 0.487874 | 00:01 |
现在真令人失望……我们之前的单层 RNN 表现更好。为什么?原因是我们有一个更深层次的模型,导致 激活爆炸或消失。
爆炸或消失的激活
在实践中,很难从这种 RNN 中创建准确的模型。如果我们detach减少调用次数并拥有更多层,我们将获得更好的结果——这使我们的 RNN 有更长的学习时间范围和更丰富的特征来创建。但这也意味着我们有更深层次的模型需要训练。深度学习发展的主要挑战是弄清楚如何训练这些类型的模型。
这是具有挑战性的,因为当您多次乘以矩阵时会发生什么。想一想当你乘以一个数很多次时会发生什么。例如,如果你乘以 2,从 1 开始,你会得到序列 1, 2, 4, 8, ... 并且在 32 步之后,你已经是 4,294,967,296。如果乘以 0.5,会发生类似的问题:得到 0.5、0.25、0.125……32 步后,结果为 0.00000000023。如您所见,乘以一个甚至略高于或低于 1 的数字都会导致我们的起始数字在几次重复乘法后爆炸或消失。
因为矩阵乘法只是将数字相乘并将它们相加,所以重复矩阵乘法会发生完全相同的事情。这就是深度神经网络的全部——每个额外的层都是另一个矩阵乘法。这意味着深度神经网络很容易以极大或极小的数字结束。
这是一个问题,因为计算机存储数字的方式(称为 浮点数)意味着数字离零越远,它们的准确性就会越来越低。图 12-8中的图表 来自优秀的文章 “关于浮点你从未想知道但将被迫找出答案”,显示了浮点数的精度如何随数轴变化。

图 12-8。浮点数的精度
这种不准确性意味着,对于深度网络,为更新权重而计算的梯度通常最终为零或无穷大。这通常被称为梯度消失或梯度爆炸问题。这意味着在 SGD 中,权重要么根本不更新,要么跳到无穷大。无论哪种方式,他们都不会通过培训得到改善。
研究人员已经开发出解决这个问题的方法,我们将在本书后面讨论。一种选择是以一种不太可能发生爆炸激活的方式更改层的定义。我们将在第 13 章讨论批量归一化时以及第 14 章讨论 ResNet 时详细介绍如何完成此操作,尽管这些细节在实践中通常并不重要(除非您是正在创建的研究人员)解决这个问题的新方法)。处理这个问题的另一种 策略是注意初始化,这是我们将在第 17 章研究的主题。
对于 RNN,经常使用两种类型的层来避免激活爆炸:门控循环单元(GRU) 和 长短期记忆(LSTM) 层。这两个都在 PyTorch 中可用,并且是 RNN 层的直接替代品。我们将在本书中仅介绍 LSTM;许多优秀的在线教程解释了 GRU,它是 LSTM 设计的一个小变体。
长短期记忆网络
LSTM 是一种架构,由 Jürgen Schmidhuber 和 Sepp Hochreiter 于 1997 年提出。在这个架构中,隐藏状态不是一个,而是两个。在我们的基础 RNN 中, 隐藏状态是 RNN 在前一个时间步的输出。该隐藏状态然后负责两件事:
-
为输出层提供正确的信息以预测正确的下一个标记
-
保留对句子中发生的一切的记忆
例如,考虑“Henry 有一只狗,他非常喜欢他的狗”和“Sophie 有一只狗,她非常喜欢她的狗”这两个句子。很明显,RNN 需要记住句子开头的名字才能预测he/she或 his/her。
在实践中,RNN 真的很不擅长保留句子中更早发生的事情的记忆,这是在 LSTM中拥有另一个隐藏状态(称为单元状态)的动机。细胞状态将负责保持长短期记忆,而隐藏状态将专注于下一个要预测的标记。让我们仔细看看这是如何实现的,并从头开始构建 LSTM。
从头开始构建 LSTM
为了构建 LSTM,我们首先必须了解其架构。 其内部结构如图 12-9所示。
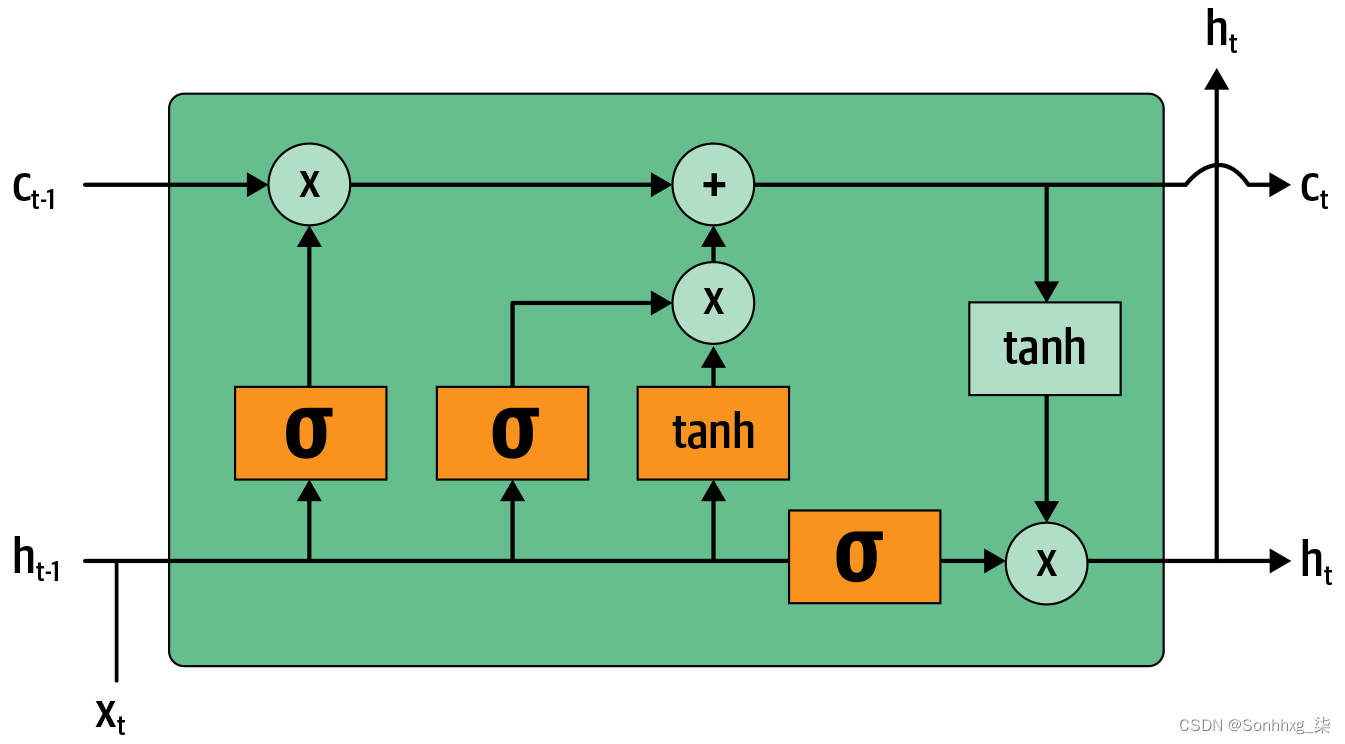
图 12-9。LSTM 的架构
在这张图片中,我们的输入Xt与先前的隐藏状态一起进入左侧(Ht-1) 和细胞状态 (Ct-1). 四个橙色框代表四个层(我们的神经网络),激活是 sigmoid(p) 或 tanh。tanh 只是一个重新缩放到 –1 到 1 范围内的 sigmoid 函数。它的数学表达式可以这样写:

在哪里p是 sigmoid 函数。图中的绿色圆圈是elementwise操作。右边出来的是新的隐藏状态(Ht) 和新的细胞状态 (Ct), 准备好我们的下一个输入。新的隐藏状态也用作输出,这就是箭头向上分裂的原因。
让我们一个一个地检查四个神经网络(称为门)并解释图表——但在此之前,请注意细胞状态(顶部)的变化非常小。它甚至不直接通过神经网络!这正是它会保持更长期状态的原因。
首先,输入和旧隐藏状态的箭头连接在一起。在本章前面写的 RNN 中,我们将它们加在一起。在 LSTM 中,我们将它们堆叠在一个大张量中。这意味着我们嵌入的维度(这是维度X吨) 可以不同于我们隐藏状态的维度。如果我们称它们 为n_inand n_hid,底部的箭头大小为n_in + n_hid;因此所有的神经网络(橙色框)都是具有 n_in + n_hid输入和n_hid 输出的线性层。
第一个门(从左往右看)叫做遗忘门。由于它是一个线性层,后面跟着一个 sigmoid,它的输出将由 0 到 1 之间的标量组成。我们将这个结果乘以细胞状态来确定保留哪些信息和丢弃哪些信息:接近 0 的值被丢弃,并且值接近 1 被保留。这使 LSTM 能够忘记其长期状态。例如,当跨越一个句点或一个xxbos标记时,我们会期望它(已经学会)重置它的细胞状态。
第二个门称为输入门。它与第三个门(实际上没有名称,但有时称为单元门)一起工作以更新单元状态。例如,我们可能会看到一个新的性别代词,在这种情况下,我们需要替换遗忘门删除的有关性别的信息。与遗忘门类似,输入门决定要更新单元状态的哪些元素(值接近 1)或不更新(值接近 0)。第三个门确定那些更新的值是什么,在 –1 到 1 的范围内(多亏了 tanh 函数)。结果被添加到细胞状态。
最后一个门是输出门。它确定使用来自细胞状态的哪些信息来生成输出。单元状态在与输出门的 sigmoid 输出组合之前经过 tanh,结果是新的隐藏状态。在代码方面,我们可以这样写相同的步骤:
class LSTMCell(Module):
def __init__(self, ni, nh):
self.forget_gate = nn.Linear(ni + nh, nh)
self.input_gate = nn.Linear(ni + nh, nh)
self.cell_gate = nn.Linear(ni + nh, nh)
self.output_gate = nn.Linear(ni + nh, nh)
def forward(self, input, state):
h,c = state
h = torch.cat([h, input], dim=1)
forget = torch.sigmoid(self.forget_gate(h))
c = c * forget
inp = torch.sigmoid(self.input_gate(h))
cell = torch.tanh(self.cell_gate(h))
c = c + inp * cell
out = torch.sigmoid(self.output_gate(h))
h = out * torch.tanh(c)
return h, (h,c)在实践中,我们可以重构代码。此外,就性能而言,进行一次大矩阵乘法比进行四次较小的矩阵乘法更好(这是因为我们只在 GPU 上启动了一次特殊的快速内核,它让 GPU 可以并行执行更多工作)。堆叠需要一点时间(因为我们必须在 GPU 上移动其中一个张量以将其全部放在一个连续的数组中),因此我们为输入和隐藏状态使用两个单独的层。优化和重构后的代码如下所示:
class LSTMCell(Module):
def __init__(self, ni, nh):
self.ih = nn.Linear(ni,4*nh)
self.hh = nn.Linear(nh,4*nh)
def forward(self, input, state):
h,c = state
# One big multiplication for all the gates is better than 4 smaller ones
gates = (self.ih(input) + self.hh(h)).chunk(4, 1)
ingate,forgetgate,outgate = map(torch.sigmoid, gates[:3])
cellgate = gates[3].tanh()
c = (forgetgate*c) + (ingate*cellgate)
h = outgate * c.tanh()
return h, (h,c)在这里,我们使用 PyTorchchunk方法将我们的张量分成四个部分。它是这样工作的:
t = torch.arange(0,10); ttensor([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
t.chunk(2)(tensor([0, 1, 2, 3, 4]), tensor([5, 6, 7, 8, 9]))
现在让我们使用这个架构来训练语言模型!
使用 LSTM 训练语言模型
这是与 相同的网络LMModel5,使用两层 LSTM。我们可以以更高的学习率、更短的时间训练它,并获得更好的准确性:
class LMModel6(Module):
def __init__(self, vocab_sz, n_hidden, n_layers):
self.i_h = nn.Embedding(vocab_sz, n_hidden)
self.rnn = nn.LSTM(n_hidden, n_hidden, n_layers, batch_first=True)
self.h_o = nn.Linear(n_hidden, vocab_sz)
self.h = [torch.zeros(n_layers, bs, n_hidden) for _ in range(2)]
def forward(self, x):
res,h = self.rnn(self.i_h(x), self.h)
self.h = [h_.detach() for h_ in h]
return self.h_o(res)
def reset(self):
for h in self.h: h.zero_()learn = Learner(dls, LMModel6(len(vocab), 64, 2),
loss_func=CrossEntropyLossFlat(),
metrics=accuracy, cbs=ModelResetter)
learn.fit_one_cycle(15, 1e-2)| epoch | train_loss | vaild_loss | accuracy | time |
|---|---|---|---|---|
| 0 | 3.000821 | 2.663942 | 0.438314 | 00:02 |
| 1 | 2.139642 | 2.184780 | 0.240479 | 00:02 |
| 2 | 1.607275 | 1.812682 | 0.439779 | 00:02 |
| 3 | 1.347711 | 1.830982 | 0.497477 | 00:02 |
| 4 | 1.123113 | 1.937766 | 0.594401 | 00:02 |
| 5 | 0.852042 | 2.012127 | 0.631592 | 00:02 |
| 6 | 0.565494 | 1.312742 | 0.725749 | 00:02 |
| 7 | 0.347445 | 1.297934 | 0.711263 | 00:02 |
| 8 | 0.208191 | 1.441269 | 0.731201 | 00:02 |
| 9 | 0.126335 | 1.569952 | 0.737305 | 00:02 |
| 10 | 0.079761 | 1.427187 | 0.754150 | 00:02 |
| 11 | 0.052990 | 1.494990 | 0.745117 | 00:02 |
| 12 | 0.039008 | 1.393731 | 0.757894 | 00:02 |
| 13 | 0.031502 | 1.373210 | 0.758464 | 00:02 |
| 14 | 0.028068 | 1.368083 | 0.758464 | 00:02 |
正则化 LSTM
一般来说,循环神经网络很难训练,因为我们之前看到过激活和梯度消失的问题。使用 LSTM(或 GRU)单元使训练比普通 RNN 更容易,但它们 仍然很容易过度拟合。数据扩充虽然有可能,但较少用于文本数据而不是图像,因为在大多数情况下它需要另一个模型来生成随机扩充(例如,通过将文本翻译成另一种语言然后再翻译回原始语言)。总的来说,文本数据的数据增强目前还没有得到很好的探索。
然而,我们可以使用其他正则化技术来减少过度拟合,这些技术在 LSTM 中被彻底研究过 Stephen Merity 等人的论文“正则化和优化 LSTM 语言模型”。这篇论文展示了如何有效地使用 dropout、激活正则化和时间激活正则化可以让 LSTM 击败以前需要更复杂模型的最先进结果。作者将使用这些技术的 LSTM 称为AWD-LSTM。我们将依次研究这些技术中的每一种。
Dropout
Dropout是一种正则化技术,由 Geoffrey Hinton 等人引入。在“通过防止特征检测器的共同适应来改善神经网络”中。基础的 想法是在训练时随机将一些激活更改为零。这确保所有神经元都积极地为输出工作, 如图 12-10 所示(来自Nitish Srivastava 等人的“Dropout:一种防止神经网络过度拟合的简单方法”)。

图 12-10。在神经网络中应用 dropout(由 Nitish Srivastava 等人提供)
Hinton 在一次采访中解释 dropout 的灵感时使用了一个很好的比喻:
我去了我的银行。出纳员一直在换,我问其中一个为什么。他说他不知道,但他们经常搬家。我想这一定是因为它需要员工之间的合作才能成功骗取银行。这让我意识到,在每个示例中随机移除不同的神经元子集可以防止阴谋论,从而减少过度拟合。
在同一次采访中,他还解释说神经科学提供了额外的 灵感:
我们真的不知道为什么神经元会发出尖峰信号。一种理论是他们想要噪音以便进行正则化,因为我们拥有的参数比我们拥有的数据点多得多。dropout 的想法是,如果你有嘈杂的激活,你可以负担得起使用更大的模型。
这解释了为什么 dropout 有助于泛化背后的想法:首先它帮助神经元更好地合作;然后它使激活更加嘈杂,从而使模型更加健壮。
然而,我们可以看到,如果我们只是将这些激活归零而不做任何其他事情,我们的模型在训练时就会出现问题:如果我们从五个激活的总和(因为我们应用了 ReLU,它们都是正数)到第二,这不会有相同的规模。因此,如果我们以概率 应用 dropout p,我们通过将它们除以1-p(平均p将归零,所以它离开 1-p)来重新缩放所有激活,如图 12-11所示。
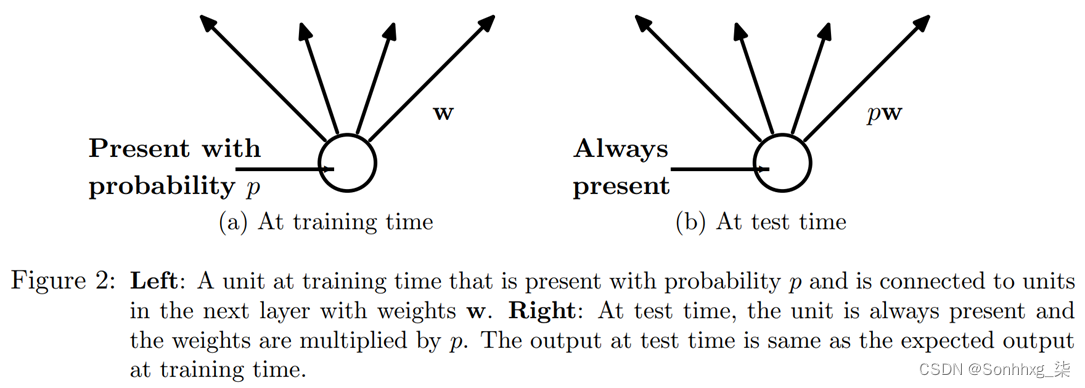
图 12-11。为什么我们在应用 dropout 时缩放激活(由 Nitish Srivastava 等人提供)
这是 PyTorch 中 dropout 层的完整实现(尽管 PyTorch 的原生层实际上是用 C 而不是 Python 编写的):
class Dropout(Module):
def __init__(self, p): self.p = p
def forward(self, x):
if not self.training: return x
mask = x.new(*x.shape).bernoulli_(1-p)
return x * mask.div_(1-p)该bernoulli_方法创建一个由随机零(概率为 )和随机零(概率为p)组成的张量,1-p然后在除以 之前将其与我们的输入相乘1-p。请注意training 属性的使用,它在任何 PyTorch 中都可用nn.Module,并告诉我们是在进行训练还是推理。
我们会在
bernoulli_这里添加一个代码示例,这样您就可以确切地看到它是如何工作的。但既然您已经足够了解自己做这件事,我们将为您做的例子会越来越少,而是希望您自己做实验来了解事情是如何运作的。在这种情况下,您会在本章末尾的调查问卷中看到我们要求您进行实验bernoulli_——但不要等到我们要求您通过实验来加深对我们正在研究的代码的理解;继续做吧!
在将 LSTM 的输出传递到最后一层之前使用 dropout 将有助于减少过度拟合。Dropout 也用于许多其他模型,包括 中使用的默认 CNN 头fastai.vision,并且可以fastai.tabular通过传递ps参数(其中每个“p”传递给每个添加的Dropout层)来使用,正如我们将在第 15 章中看到的那样。
trainingDropout在训练和验证模式下有不同的行为,我们使用Dropout. train在 a上调用方法Module设置training为True(对于您调用该方法的模块和它递归包含的每个模块),并将eval其设置为False. 这是在调用 的方法时自动完成的Learner,但如果您没有使用该类,请记住根据需要从一个类切换到另一个类。
激活正则化和时间激活正则化
激活正则化(AR) 和时间激活正则化(TAR) 是两种与权重衰减非常相似的正则化方法,将在第 8 章中讨论。当应用权重衰减时,我们对损失添加一个小的惩罚 旨在使权重尽可能小。对于激活正则化,我们将尝试使 LSTM 产生的最终激活尽可能小,而不是权重。
为了规范化最终的激活,我们必须将它们存储在某个地方,然后将它们的平方的均值添加到损失中(连同乘数alpha,就像wd权重衰减一样):
loss += alpha * activations.pow(2).mean()时间激活正则化与我们预测句子中的标记这一事实有关。这意味着当我们按顺序阅读 LSTM 的输出时,它们的输出可能会有些意义。TAR 通过对损失添加惩罚来鼓励这种行为,以使两个连续激活之间的差异尽可能小:我们的激活张量具有形状bs x sl x n_hid,并且我们在序列长度轴(中间的维度)上读取连续激活). 有了这个,TAR 可以表示如下:
loss += beta * (activations[:,1:] - activations[:,:-1]).pow(2).mean()alpha然后beta是两个要调整的超参数。为了使这项工作正常进行,我们需要带 dropout 的模型返回三样东西:正确的输出、LSTM pre-dropout 的激活以及 LSTM post-dropout 的激活。AR 通常应用于丢失的激活(为了不惩罚我们之后变成零的激活),而 TAR 应用于非丢失的激活(因为这些零在两个连续的时间步长之间产生很大差异)。然后调用的回调RNNRegularizer将为我们应用此正则化。
训练权重绑定正则化 LSTM
我们可以将 dropout(在我们进入输出层之前应用)与 AR 和 TAR 结合起来训练我们之前的 LSTM。我们只需要 返回三样东西而不是一件:LSTM 的正常输出、丢弃的激活和 LSTM 的激活。最后两个将由回调拾取,因为 RNNRegularization它必须对损失做出贡献。
我们可以从AWD-LSTM 论文中添加的另一个有用技巧是权重绑定。在语言模型中,输入嵌入表示一个映射 从英语单词到激活,输出隐藏层表示从激活到英语单词的映射。我们可能会直觉地期望这些映射可能是相同的。我们可以通过为这些层中的每一层分配相同的权重矩阵来在 PyTorch 中表示这一点:
self.h_o.weight = self.i_h.weight在LMModel7中,我们包括这些最终调整:
class LMModel7(Module):
def __init__(self, vocab_sz, n_hidden, n_layers, p):
self.i_h = nn.Embedding(vocab_sz, n_hidden)
self.rnn = nn.LSTM(n_hidden, n_hidden, n_layers, batch_first=True)
self.drop = nn.Dropout(p)
self.h_o = nn.Linear(n_hidden, vocab_sz)
self.h_o.weight = self.i_h.weight
self.h = [torch.zeros(n_layers, bs, n_hidden) for _ in range(2)]
def forward(self, x):
raw,h = self.rnn(self.i_h(x), self.h)
out = self.drop(raw)
self.h = [h_.detach() for h_ in h]
return self.h_o(out),raw,out
def reset(self):
for h in self.h: h.zero_()Learner我们可以使用RNNRegularizer 回调创建正则化:
learn = Learner(dls, LMModel7(len(vocab), 64, 2, 0.5),
loss_func=CrossEntropyLossFlat(), metrics=accuracy,
cbs=[ModelResetter, RNNRegularizer(alpha=2, beta=1)])ATextLearner自动为我们添加这两个回调(使用默认值alpha和beta默认值),因此我们可以简化前面的行:
learn = TextLearner(dls, LMModel7(len(vocab), 64, 2, 0.4),
loss_func=CrossEntropyLossFlat(), metrics=accuracy)然后我们可以训练模型,并通过将权重衰减增加到 来添加额外的正则化0.1:
learn.fit_one_cycle(15, 1e-2, wd=0.1)| epoch | train_loss | vaild_loss | accuracy | time |
|---|---|---|---|---|
| 0 | 2.693885 | 2.013484 | 0.466634 | 00:02 |
| 1 | 1.685549 | 1.187310 | 0.629313 | 00:02 |
| 2 | 0.973307 | 0.791398 | 0.745605 | 00:02 |
| 3 | 0.555823 | 0.640412 | 0.794108 | 00:02 |
| 4 | 0.351802 | 0.557247 | 0.836100 | 00:02 |
| 5 | 0.244986 | 0.594977 | 0.807292 | 00:02 |
| 6 | 0.192231 | 0.511690 | 0.846761 | 00:02 |
| 7 | 0.162456 | 0.520370 | 0.858073 | 00:02 |
| 8 | 0.142664 | 0.525918 | 0.842285 | 00:02 |
| 9 | 0.128493 | 0.495029 | 0.858073 | 00:02 |
| 10 | 0.117589 | 0.464236 | 0.867188 | 00:02 |
| 11 | 0.109808 | 0.466550 | 0.869303 | 00:02 |
| 12 | 0.104216 | 0.455151 | 0.871826 | 00:02 |
| 13 | 0.100271 | 0.452659 | 0.873617 | 00:02 |
| 14 | 0.098121 | 0.458372 | 0.869385 | 00:02 |
结论
您现在已经了解了我们在第 10 章的文本分类中使用的 AWD-LSTM 架构中的所有内容。它在更多地方使用了 dropout:
-
Embedding dropout(在嵌入层内,丢弃一些随机的嵌入行)
-
输入丢失(在嵌入层之后应用)
-
权重丢失(在每个训练步骤应用于 LSTM 的权重)
-
Hidden dropout(应用于两层之间的隐藏状态)
这使得它更加规范化。由于微调这五个 dropout 值(包括输出层之前的 dropout)很复杂,我们已经确定了良好的默认值,并允许使用drop_mult您在该章中看到的参数(乘以每个 dropout)来整体调整 dropout 的大小).
![[附源码]SSM计算机毕业设计8号体育用品销售及转卖系统JAVA](https://img-blog.csdnimg.cn/40f0eab89c4c4c6b8a9cb272e33750f7.png)




![[附源码]Python计算机毕业设计 校园疫情防控系统](https://img-blog.csdnimg.cn/a55a42dd06fa4f72be7bb8e3d80e7e38.png)