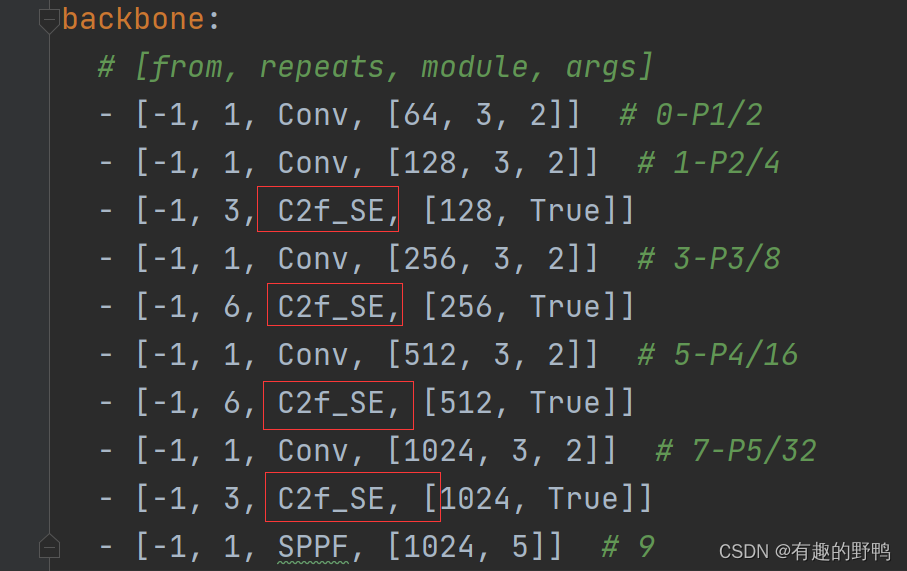
多种注意力表格：
大神参考仓库链接： 魔鬼面具
对应 name 就是目录，点击即可跳转到对应学习。

name	need_chaneel	paper
SE (2017)	True	https://arxiv.org/abs/1709.01507
BAM (2018)	True	https://arxiv.org/pdf/1807.06514.pdf
CBAM (2018)	True	https://openaccess.thecvf.com/content_ECCV_2018/papers/Sanghyun_Woo_Convolutional_Block_Attention_ECCV_2018_paper.pdf
CoTAttention (2021)	True	https://arxiv.org/abs/2107.12292
MobileViTAttention (2021)	True	https://arxiv.org/abs/2110.02178
SK	True	https://arxiv.org/pdf/1903.06586.pdf
ShuffleAttention	True	https://arxiv.org/pdf/2102.00240.pdf
S2Attention	True	https://arxiv.org/abs/2108.01072
ParNetAttention	True	https://arxiv.org/abs/2110.07641
CoordAttention	True	https://arxiv.org/abs/2103.02907
MHSA Multi-Head-Self-Attention	True	https://wuch15.github.io/paper/EMNLP2019-NRMS.pdf
A2Attention	True	https://arxiv.org/pdf/1810.11579.pdf
GC Global Context Attention	True	https://arxiv.org/abs/1904.11492
EffectiveSE Effective Squeeze-Excitation	True	https://arxiv.org/abs/1911.06667
GE Gather-Excite Attention	True	https://arxiv.org/abs/1810.12348
CrissCrossAttention	True	https://arxiv.org/abs/1811.11721
Polarized Self-Attention	True	https://arxiv.org/abs/2107.00782
Sequential Self-Attention	True	https://arxiv.org/abs/2107.00782
GAM	True	https://arxiv.org/pdf/2112.05561v1.pdf
Biformer	True	https://arxiv.org/abs/2303.08810
EMA	True	https://arxiv.org/abs/2305.13563v2
CloAttention	True	https://arxiv.org/abs/2303.17803
LSKBlock	True	https://arxiv.org/pdf/2303.09030.pdf
ECA (2020)	False	https://arxiv.org/pdf/1910.03151.pdf
SimAM (2021)	False	http://proceedings.mlr.press/v139/yang21o/yang21o.pdf
SGE	False	https://arxiv.org/pdf/1905.09646.pdf
TripletAttention	False	https://arxiv.org/abs/2010.03045

  注意：博客尽可能的简单的介绍各个注意力主要的思想和图示，并通过代码的解释和测试来详细的理解各个注意力机制的使用。(内容可能不全，希望各位理解)

SE

全称：Squeeze-and-Excitation 挤压和激励
1、主要思想：想通过全局池化和全链接，形成通道上的注意力。然后从通道域的角度赋予图像不同位置不同的权重，得到更重要的特征信息。
简单来说：将原始特征图H 、W 维度上压缩为为1、1(长条形状)，再进行一些全链接层， 得到1 * 1 * C的条形，再和原始的特征图进行通道上的相称，得到最终的注意力特征层。

对应公式具体流程如下：
$$\begin{gathered} \hat{X}=F_{scale()}(U,F_{ex}(F_{sq}(U),W)) \\ {F}_{sq}(U)=AvgPool(U),F_{ex}=MLP. \end{gathered}$$

值得注意的地方：1、论文中对比了平均池化与最大池化的实验结果，发现平均池化效果稍好一些（后面一些注意力机制，两者都用）。2、SE 的如何防止才可以使得网络的性能最优，论文中也在探讨。

2、模块使用地方：SE模块是一个即插即用的模块，可以在卷积模块之后直接插入SE模块，也可以在残差结构里面添加了SE模块。

3、代码

import numpy as np
import torch
from torch import nn
from torch.nn import init

class SEAttention(nn.Module):

    def __init__(self, channel=512, reduction=16):
        super().__init__()
        # 对应全局平均池化
        self.avg_pool = nn.AdaptiveAvgPool2d(1)
        
        # 两层全连接层，用于获取通道注意力机制，最后用 Sigmoid 激活函数，输出 0~1 之间的权重
        self.fc = nn.Sequential(
            nn.Linear(channel, channel // reduction, bias=False),
            nn.ReLU(inplace=True),
            nn.Linear(channel // reduction, channel, bias=False),
            nn.Sigmoid()
        )

    def init_weights(self):
        for m in self.modules():
            if isinstance(m, nn.Conv2d):
                init.kaiming_normal_(m.weight, mode='fan_out')
                if m.bias is not None:
                    init.constant_(m.bias, 0)
            elif isinstance(m, nn.BatchNorm2d):
                init.constant_(m.weight, 1)
                init.constant_(m.bias, 0)
            elif isinstance(m, nn.Linear):
                init.normal_(m.weight, std=0.001)
                if m.bias is not None:
                    init.constant_(m.bias, 0)

    def forward(self, x):
        b, c, _, _ = x.size()
        y = self.avg_pool(x).view(b, c)
        y = self.fc(y).view(b, c, 1, 1)
        return x * y.expand_as(x)


if __name__ == '__main__':
    input=torch.randn(50,512,7,7)
    se = SEAttention(channel=512,reduction=8)
    output=se(input)
    print(output.shape)

BAM

全称：Bottleneck Attention Module 瓶颈注意模块
1、主要思想：沿着两个不同的路径（通道和空间）推断注意力映射，通道注意力使得网络关注那个通道上的数据更加重要，空间注意力机制使得网络关注那个位置上的数据更加重要。
简单来说：一个分支将原始特征图H 、W 维度上压缩为为1、1(长条形状)，再进行一些全链接层， 得到C * 1 * 1的条形。另一个分支将在通道C上进行压缩，压缩为C/R (R为比例)(拍扁一些)，再经过一些卷积层，得到1 * H * W的特征图。将C * 1 * 1 对应乘上1 * H * W， 就变成 C * H * W 的 BAM 注意力。再和原始特征图对应相乘，经过残差层即可。对应图示如下：

对应公式具体流程如下：
$$\begin{gathered} M_c(F)=BN(MLP(AvgPool(F)))=BN(W_1(W_{0}AvgPool(F)+b_0)+b_1), \\ {M}_s(F)=BN(f_3^{1\times 1}(f_2^{3\times 3}(f_1^{3\times 3}(f_0^{1\times 1}(F))))), \\ M(F)=\sigma (M_c(F)+M_s(F)), \\ {F}^{\prime }=F+F\otimes M(F), \\ 1、其中，F\in R^{C\ast H\ast W},AvgPool(F)\in R^{C\ast 1\ast 1},W_0\in R^{C/r\times C},b_0\in R^{C/r},W_1\in R^{C\times C/r},b_1\in R^C. \\ 2、其中，f_0^{1\times 1}\in R^{C\ast 1\ast 1},f_1^{3\times 3}\in R^{C/r\ast 3\ast 3},f_2^{3\times 3}\in R^{C/r\ast 3\ast 3},f_3^{1\times 1}\in R^{C/r\ast 1\ast 1}, \\ {f}_0^{1\times 1}\ast C/r个，f_1^{3\times 3}\ast C/r个，f_2^{3\times 3}\ast C/r个，f_0^{1\times 1}\ast 1个， \\ 3、其中，M_c(F)+M_s(F)在相加之前都被调整为R^{C\times H\times W}大小。 \\ 4、其中，\otimes 表示逐元素乘法。 \end{gathered}$$
值得注意的点是：模块有两个超参数：膨胀值 d 和收缩比 r。膨胀值决定了接受域的大小，有助于空间分支的上下文信息聚集。收缩比控制着两个注意力分支的能力和开销。 通过实验验证，设 d = 4, r = 16。

2、模块使用地方：将模块放在模型的每个瓶颈处（特征映射产生降采样的地方），构建一个具有多个参数的分层注意，可以与任何前馈模型以端到端方式进行训练。

3、代码

import numpy as np
import torch
from torch import nn
from torch.nn import init

def autopad(k, p=None, d=1):  # kernel, padding, dilation
    """Pad to 'same' shape outputs."""
    if d > 1:
        k = d * (k - 1) + 1 if isinstance(k, int) else [d * (x - 1) + 1 for x in k]  # actual kernel-size
    if p is None:
        p = k // 2 if isinstance(k, int) else [x // 2 for x in k]  # auto-pad
    return p

class Flatten(nn.Module):
    def forward(self, x):
        return x.view(x.shape[0], -1)

class ChannelAttention(nn.Module):
    def __init__(self, channel, reduction=16, num_layers=3):
        super().__init__()
        # 添加通道注意力机制的通道数，方便后面的全连接层
        gate_channels = [channel]
        gate_channels += [channel // reduction] * num_layers
        gate_channels += [channel]
        
        # 全局平均池化，用于降维为 B * C * 1 * 1
        self.avgpool = nn.AdaptiveAvgPool2d(1)
        
        self.ca = nn.Sequential()
        
        # 展平，用于全连接层 B * C * 1 * 1 -> B * C
        self.ca.add_module('flatten', Flatten())
        
        # 连续的全链接层，来获取通道注意力机制 
        for i in range(len(gate_channels) - 2):
            self.ca.add_module('fc%d' % i, nn.Linear(gate_channels[i], gate_channels[i + 1]))
            self.ca.add_module('bn%d' % i, nn.BatchNorm1d(gate_channels[i + 1]))
            self.ca.add_module('relu%d' % i, nn.ReLU())
            
        # 最后的全连接层，用于恢复通道数为 B * C.
        self.ca.add_module('last_fc', nn.Linear(gate_channels[-2], gate_channels[-1]))

    def forward(self, x):
        res = self.avgpool(x)
        res = self.ca(res)
        # unsqueeze(-1).unsqueeze(-1) 的作用是为了将 B * C 转换为 B * C * 1 * 1，方便后面的广播。
        # expand_as(x) 的作用是为了将 B * C * 1 * 1 广播为 B * C * H * W
        res = res.unsqueeze(-1).unsqueeze(-1).expand_as(x)
        return res


class SpatialAttention(nn.Module):
    def __init__(self, channel, reduction=16, num_layers=3, dia_val=2):
        super().__init__()
        self.sa = nn.Sequential()
        # 最开始的 1x1 卷积，用于降维为原来的 1/r
        self.sa.add_module('conv_reduce1',
                           nn.Conv2d(kernel_size=1, in_channels=channel, out_channels=channel // reduction))
        self.sa.add_module('bn_reduce1', nn.BatchNorm2d(channel // reduction))
        self.sa.add_module('relu_reduce1', nn.ReLU())
        
        # 连续的 3x3 的空洞卷积， 用于捕捉空间信息
        for i in range(num_layers):
            self.sa.add_module('conv_%d' % i, nn.Conv2d(kernel_size=3, in_channels=channel // reduction,
                                                        out_channels=channel // reduction, padding=autopad(3, None, dia_val), dilation=dia_val))
            self.sa.add_module('bn_%d' % i, nn.BatchNorm2d(channel // reduction))
            self.sa.add_module('relu_%d' % i, nn.ReLU())
            
        # 最后的 1x1 卷积，用于恢复通道数
        self.sa.add_module('last_conv', nn.Conv2d(channel // reduction, 1, kernel_size=1))

    def forward(self, x):
        res = self.sa(x)
        res = res.expand_as(x)
        return res


class BAMBlock(nn.Module):
    def __init__(self, channel=512, reduction=16, dia_val=2):
        super().__init__()
        self.ca = ChannelAttention(channel=channel, reduction=reduction)
        self.sa = SpatialAttention(channel=channel, reduction=reduction, dia_val=dia_val)
        self.sigmoid = nn.Sigmoid()

    def init_weights(self):
        # 根据不同的网络初始化权重
        for m in self.modules():
            if isinstance(m, nn.Conv2d):
                init.kaiming_normal_(m.weight, mode='fan_out')
                if m.bias is not None:
                    init.constant_(m.bias, 0)
            elif isinstance(m, nn.BatchNorm2d):
                init.constant_(m.weight, 1)
                init.constant_(m.bias, 0)
            elif isinstance(m, nn.Linear):
                init.normal_(m.weight, std=0.001)
                if m.bias is not None:
                    init.constant_(m.bias, 0)

    def forward(self, x):
        # b, c, _, _ = x.size()
        sa_out = self.sa(x)
        ca_out = self.ca(x)
        weight = self.sigmoid(sa_out + ca_out)
        out = (1 + weight) * x
        return out

if __name__ == '__main__':
    input = torch.randn(50, 512, 7, 7)
    bam = BAMBlock(channel=512, reduction=16, dia_val=2)
    output = bam(input)
    print(output.shape)

CBAM

注意：和BAM的不一样，BAM模块是放在网络的每个瓶颈处，CBAM放在每个卷积块上。
全称：Convolutional Block Attention Module 卷积块注意力模块
1、主要思想：沿着一条路径路径推断注意力映射，先执行通道注意力模块，和原始特征图相乘之后，再执行空间注意力模块，再和原始特征层相乘。通道注意力使得网络关注那个通道上的数据更加重要，空间注意力机制使得网络关注那个位置上的数据更加重要。
简单来说，

对应公式流程如下：
$$\begin{gathered} F^{\prime }=M_c(F)\otimes F, \\ {F}^{\prime \prime }=M_s(F^{\prime })\otimes F^{\prime }, \\ 其中，F、F^{\prime }、F^{\prime \prime }\in R^{C\times H\times W},M_c(F)\in R^{1\times H\times W},M_s(F^{\prime })\in R^{C\times 1\times 1}, \end{gathered}$$
其中⊗表示基于元素的乘法。在乘法过程中，注意值被广播(复制):通道注意值沿着空间维度广播，反之亦然。F”是最终的精炼输出。

细化两个注意力模块：
1、通道注意力模块：在 H * W 的维度上，利用平均池化和最大池化操作聚合特征映射的空间信息，生成两种不同的空间上下文描述符，经过共享MLP 之后，再相加经过 sigmoid，得到最终的通道注意力机制。(SE 注意力中只要的全局平均池化，这里全都要)
也就是说：由于feature map的每个通道都被认为是一个特征检测器，所以通道的注意力集中在给定一个输入图像的“什么”是有意义的。

2、空间注意力机制：在 C 的维度上，分别得到全局平均池化和平均池化的结果，进行叠加，为B * 2 * H * W，再经过卷积提取、压缩一些信息，通过 sigmoid 之后得到 空间注意力机制。(和 BAM 不一样的地方，没有使用 1 * 1 的卷积来降维，而是采用了 池化的方式)

对应公式流程：
$$\begin{gathered} 通道注意力 \\ {M}_c(F)=\sigma (MLP(AvgPool(F))+MLP(MaxPool(F))) \\ =\sigma (W_1(W_0(F_{avg}^c))+W_1(W_0(F_{max}^c))), \\ 其中，\sigma 为sigmoid函数，W_0\in R^{C/r\times C},W_1\in R^{C\times C/r}， \\ 空间注意力 \\ {M}_s(F)=\sigma (f^{7\times 7}([AvgPool(F);MaxPool(F)])) \\ =\sigma (f^{7\times 7}([F_{avg}^s;F_{max}^s])), \\ 其中，其中\sigma 为sigmoid函数，f^{7\times 7}为为7\times 7的卷积。 \end{gathered}$$

值得注意的是：
1、空间注意力的时候，使用的为 7 * 7 的卷积，r 为 16 。
2、在实际实现通道注意力的时候，因为 MLP 是共享的，我们输入有两个，所以这里可以使用 1 * 1 的卷积来实现 MLP 的效果，但是可以很方便的实现参数共享。其次为了减少参数开销，隐藏的激活大小设置为$R^{C/r\times 1\times 1}$，其中r是减少率。
3、论文实验证实，同时使用平均池和最大池特性这两个特性比单独使用它们大大提高了网络的表示能力。
4、注意模块的安排。给定一个输入图像，两个注意模块，通道和空间，计算互补注意，分别关注“什么”和“在哪里”。考虑到这一点，两个模块可以以并行或顺序的方式放置。我们发现序列排列比并行排列有更好的结果。对于顺序过程的排列，我们的实验结果表明，信道优先顺序略好于空间优先顺序。
5、在VOC数据集上，作者将SE和CBAM放在每个分类器的前面，在预测之前细化由上采样的全局特征和相应的局部特征组成的最终特征，强制模型自适应地只选择有意义的特征。

2、模块使用地方：CBAM放在每个卷积块上，可以使用在网络的任何地方。
下面的方法是在残差结构内部使用：

3、代码

import numpy as np
import torch
from torch import nn
from torch.nn import init


class ChannelAttention(nn.Module):
    def __init__(self, channel, reduction=16):
        super().__init__()
        # 两种全局池化方式 + 共享的两层全连接层(1 * 1 卷积相当于全连接层)
        self.maxpool = nn.AdaptiveMaxPool2d(1)
        self.avgpool = nn.AdaptiveAvgPool2d(1)
        self.se = nn.Sequential(
            nn.Conv2d(channel, channel // reduction, 1, bias=False),
            nn.ReLU(),
            nn.Conv2d(channel // reduction, channel, 1, bias=False)
        )
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        max_result = self.maxpool(x)
        avg_result = self.avgpool(x)
        max_out = self.se(max_result)
        avg_out = self.se(avg_result)
        output = self.sigmoid(max_out + avg_out)
        return output


class SpatialAttention(nn.Module):
    def __init__(self, kernel_size=7):
        super().__init__()
        self.conv = nn.Conv2d(2, 1, kernel_size=kernel_size, padding=kernel_size // 2)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        # 1 代表通道维度，输入为 B * C * H * W
        max_result, _ = torch.max(x, dim=1, keepdim=True)
        avg_result = torch.mean(x, dim=1, keepdim=True)
        result = torch.cat([max_result, avg_result], 1)
        output = self.conv(result)
        output = self.sigmoid(output)
        return output


class CBAMBlock(nn.Module):

    def __init__(self, channel=512, reduction=16, kernel_size=7):
        super().__init__()
        self.ca = ChannelAttention(channel=channel, reduction=reduction)
        self.sa = SpatialAttention(kernel_size=kernel_size)

    def init_weights(self):
        for m in self.modules():
            if isinstance(m, nn.Conv2d):
                init.kaiming_normal_(m.weight, mode='fan_out')
                if m.bias is not None:
                    init.constant_(m.bias, 0)
            elif isinstance(m, nn.BatchNorm2d):
                init.constant_(m.weight, 1)
                init.constant_(m.bias, 0)
            elif isinstance(m, nn.Linear):
                init.normal_(m.weight, std=0.001)
                if m.bias is not None:
                    init.constant_(m.bias, 0)

    def forward(self, x):
        b, c, _, _ = x.size()
        out = x * self.ca(x)
        out = out * self.sa(out)
        return out


if __name__ == '__main__':
    input = torch.randn(50, 512, 7, 7)
    kernel_size = input.shape[2]
    cbam = CBAMBlock(channel=512, reduction=16, kernel_size=kernel_size)
    output = cbam(input)
    print(output.shape)

CoTAttention

全称：Contextual Transformer Attention 上下文自注意力

背景提要：传统的用于视觉任务的transformer结构大多是利用$1\ast 1$ 卷积得到$Query、Key、Value$，,然后通过简单的相乘，得到注意力矩阵，这种构造方法并并没有考虑到 $Key$ 矩阵相邻位置之间丰富的上下文.( $1\ast 1$ 矩阵没有空间上的上下文)

1、主要思想：首先通过3×3卷积上下文编码得到$key$，得到静态的上下文表示。我们进一步将编码后的 $Key$ 与原始特征图上的 $Query$ 连接起来，通过两个连续的 $1\ast 1$ 卷积学习动态多头注意矩阵 $Weights$。对于 $Value$，我们通过 $1\ast 1$ 的卷积获得，然后将学习到的注意矩阵 $Weights$ 与输入值 $Values$ 相乘，实现输入的动态上下文表示。最后将静态和动态语境表示的相加融合作为输出。

简单图示如下：

细节图示对比如下：

上图(a)是作者介绍的传统的局部多头自注意力机制, 这里插播一下传统的局部多头自注意力机制的计算过程：

假设：输入:$X\in R^{H\ast W\ast C}$， 有 $C_h$ 个注意力头， 每个特征点和 $k\ast k$ 范围的点做注意力。

• 第一步：先得到 Query、Key、Value。$Q=X{W}_q,K=X{W}_k,V=X{W}_v$
• 第二步：得到 注意力。$R=K\otimes Q$
• 第三步：得到 注意力 + 位置编码。$\hat{R}=R+P\otimes Q$ 。其中, $P\in R^{k\times k\times C_k}$ 表示每个 $k\times k$ 网格内的 2D 相对位置嵌入，并且在所有 $C_h$ 头之间共享。
• 第四步：得到归一化之后的注意力机制。$A=Softmax(\hat{R})$
• 第五步：乘上 Value 得到最终的输出。 $Y=V\otimes A$

注意，论文中 $\otimes$ 被定义为：每个查询与空间中局部 k×k 网格内相应键之间的关系。我这里暂时理解为 每个特征点的描述子为 $C_k$ 维度，对应位置相乘为 $C_k\ast C_k$，然后加在一起。

上图(b)即为作者提出的Cot模块的实现过程：

• 第一步：获取 $Q、K、V$。-> $K=X,Q=X,V=X{W}_v$
• 第二步：获取静态上下文 $K^1$。不同于图(a)采用1x1的卷积生成key矩阵，CoT模块首先采用 $k\ast k$ 的卷积提取上下文信息，这样得到的$K^1$自然的可以反映近邻间的上下文信息，我们将其作为输入X的 静态上下文 表示。
• 第三步：获取 $A$ 注意力矩阵。将 $K^1$与 $Q$ 拼接起来,并且通过两个 $1\ast 1$ 的卷积计算注意力矩阵 $A=[K^1,Q]W_{\theta }{W}_{\delta }$。这样得到的注意力矩阵 $A$ 是通过 query 与 提取了上下文信息的 $k^1$ 学习所得到的，并不是仅仅通过独立的query-key对得到的。也就是通过引入静态上下文表示增强了自注意力机制。
• 第四步：获取 动态上下文表示 ： $K^2=A\otimes V$。
• 第五步：CoT 模块 最终输出：CoT模块最终的输出为静态上下文表示 $K^1$ 和动态上下文表示 $K^2$ 的融合，

值得注意的是：
1、$K^1$ 和 $K^2$ 的融合，在代码里作者采用的是SE注意力模块进行特征的融合，也可以使用相加的方式。
2、$W_{\theta }$带ReLU激活函数，$W_{\delta }$ 不带激活函数.

2、模块使用地方：
作者设计的CoT模块是一个统一的 self-attention 块，可以直接用来代替 $3\ast 3$卷积。也就是只要是 $3\ast 3$卷积 出现的地方，你都可以替换。

3、代码

import torch
from torch import nn
from torch.nn import init
from torch.nn import functional as F


class CoTAttention(nn.Module):

    def __init__(self, dim=512, kernel_size=3):
        super().__init__()
        self.dim = dim
        self.kernel_size = kernel_size

        # 用来生成静态上下文 K^1
        self.key_embed = nn.Sequential(
            nn.Conv2d(dim, dim, kernel_size=kernel_size, padding=kernel_size // 2, groups=4, bias=False),
            nn.BatchNorm2d(dim),
            nn.ReLU()
        )
        
        # 用来生成 V
        self.value_embed = nn.Sequential(
            nn.Conv2d(dim, dim, 1, bias=False),
            nn.BatchNorm2d(dim)
        )

        # 用来对 K^1 + Q 进行注意力计算,也就是使用 1 * 1的卷积来计算注意力
        # 这里和传统的自注意力采用q和k相乘不一样，这里采用q和k相加，然后再计算注意力
        factor = 4
        self.attention_embed = nn.Sequential(
            nn.Conv2d(2 * dim, 2 * dim // factor, 1, bias=False),
            nn.BatchNorm2d(2 * dim // factor),
            nn.ReLU(),
            nn.Conv2d(2 * dim // factor, kernel_size * kernel_size * dim, 1)
        )

        def init_weights(self):
            for m in self.modules():
                if isinstance(m, nn.Conv2d):
                    init.kaiming_normal_(m.weight, mode='fan_out')
                    if m.bias is not None:
                        init.constant_(m.bias, 0)
                elif isinstance(m, nn.BatchNorm2d):
                    init.constant_(m.weight, 1)
                    init.constant_(m.bias, 0)
                elif isinstance(m, nn.Linear):
                    init.normal_(m.weight, std=0.001)
                    if m.bias is not None:
                        init.constant_(m.bias, 0)

    def forward(self, x):
        bs, c, h, w = x.shape
        k1 = self.key_embed(x)  # bs,c,h,w
        v = self.value_embed(x).view(bs, c, -1)  # bs,c,h*w
        y = torch.cat([k1, x], dim=1)  # bs,2c,h,w
        att = self.attention_embed(y)  # bs,c*k*k,h,w
        att = att.reshape(bs, c, self.kernel_size * self.kernel_size, h, w)
        att = att.mean(2, keepdim=False).view(bs, c, -1)  # bs,c,h*w
        k2 = F.softmax(att, dim=-1) * v
        k2 = k2.view(bs, c, h, w)

        return k1 + k2


if __name__ == '__main__':
    input = torch.randn(50, 512, 7, 7)
    cot = CoTAttention(dim=512, kernel_size=3)
    output = cot(input)
    print(output.shape)

MobileViTAttention

全称：MobileViT 这个轻量型网络中所提出来的概念。

1、主要思想：使用CNN和transformer混合的方式，使用CNN提取局部特征，使用transformer提取全局特征。理论上网络的感受野为H*W，即全感受野。

具体来说，我们引入了 MobileViT 块，它可以有效地在张量中编码局部和全局信息。与 ViT 及其变体（带或不带卷积）不同，MobileViT 提出了学习全局表示的不同视角。标准卷积涉及三个操作：展开、局部处理和折叠。 MobileViT 块用使用转换器的全局处理取代了卷积中的局部处理。这使得 MobileViT 块具有类似 CNN 和 ViT 的属性，这有助于它用更少的参数和简单的训练方法（例如，基本增强）学习更好的表示.

图示如下：

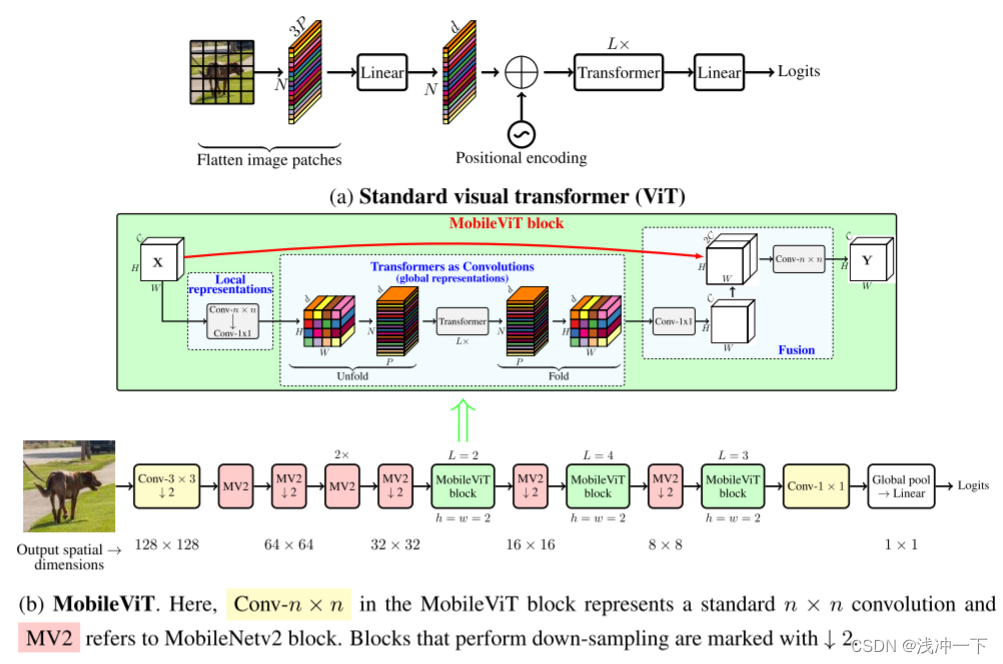
所提出模型的优点：1、 更好的性能。2、泛化能力强。3、鲁棒性强

值得注意的是：对transformer的输入保留了维度patch，每个patch包含所有像素的位置顺序。这使得encoder的输入包含了每个patch的顺序以及每个patch中所有像素的顺序。

2、模块使用地方：

3、代码

from torch import nn
import torch
from einops import rearrange


class PreNorm(nn.Module):
    def __init__(self, dim, fn):
        super().__init__()
        self.ln = nn.LayerNorm(dim)
        self.fn = fn

    def forward(self, x, **kwargs):
        return self.fn(self.ln(x), **kwargs)


class FeedForward(nn.Module):
    def __init__(self, dim, mlp_dim, dropout):
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(dim, mlp_dim),
            nn.SiLU(),
            nn.Dropout(dropout),
            nn.Linear(mlp_dim, dim),
            nn.Dropout(dropout)
        )

    def forward(self, x):
        return self.net(x)


class Attention(nn.Module):
    def __init__(self, dim, heads, head_dim, dropout):
        super().__init__()
        inner_dim = heads * head_dim
        project_out = not (heads == 1 and head_dim == dim)

        self.heads = heads
        self.scale = head_dim ** -0.5

        self.attend = nn.Softmax(dim=-1)
        self.to_qkv = nn.Linear(dim, inner_dim * 3, bias=False)

        self.to_out = nn.Sequential(
            nn.Linear(inner_dim, dim),
            nn.Dropout(dropout)
        ) if project_out else nn.Identity()

    def forward(self, x):
        qkv = self.to_qkv(x).chunk(3, dim=-1)
        q, k, v = map(lambda t: rearrange(t, 'b p n (h d) -> b p h n d', h=self.heads), qkv)
        dots = torch.matmul(q, k.transpose(-1, -2)) * self.scale
        attn = self.attend(dots)
        out = torch.matmul(attn, v)
        out = rearrange(out, 'b p h n d -> b p n (h d)')
        return self.to_out(out)


class Transformer(nn.Module):
    def __init__(self, dim, depth, heads, head_dim, mlp_dim, dropout=0.):
        super().__init__()
        self.layers = nn.ModuleList([])
        for _ in range(depth):
            self.layers.append(nn.ModuleList([
                PreNorm(dim, Attention(dim, heads, head_dim, dropout)),
                PreNorm(dim, FeedForward(dim, mlp_dim, dropout))
            ]))

    def forward(self, x):
        out = x
        for att, ffn in self.layers:
            out = out + att(out)
            out = out + ffn(out)
        return out


class MobileViTAttention(nn.Module):
    def __init__(self, in_channel=3, dim=512, kernel_size=3, patch_size=7):
        super().__init__()
        self.ph, self.pw = patch_size, patch_size
        self.conv1 = nn.Conv2d(in_channel, in_channel, kernel_size=kernel_size, padding=kernel_size // 2)
        self.conv2 = nn.Conv2d(in_channel, dim, kernel_size=1)

        self.trans = Transformer(dim=dim, depth=3, heads=8, head_dim=64, mlp_dim=1024)

        self.conv3 = nn.Conv2d(dim, in_channel, kernel_size=1)
        self.conv4 = nn.Conv2d(2 * in_channel, in_channel, kernel_size=kernel_size, padding=kernel_size // 2)

    def forward(self, x):
        y = x.clone()  # bs,c,h,w

        ## Local Representation
        y = self.conv2(self.conv1(x))  # bs,dim,h,w

        ## Global Representation
        _, _, h, w = y.shape
        y = rearrange(y, 'bs dim (nh ph) (nw pw) -> bs (ph pw) (nh nw) dim', ph=self.ph, pw=self.pw)  # bs,h,w,dim
        y = self.trans(y)
        y = rearrange(y, 'bs (ph pw) (nh nw) dim -> bs dim (nh ph) (nw pw)', ph=self.ph, pw=self.pw, nh=h // self.ph,
                      nw=w // self.pw)  # bs,dim,h,w

        ## Fusion
        y = self.conv3(y)  # bs,dim,h,w
        y = torch.cat([x, y], 1)  # bs,2*dim,h,w
        y = self.conv4(y)  # bs,c,h,w

        return y


if __name__ == '__main__':
    m = MobileViTAttention(in_channel=512)
    input = torch.randn(1, 512, 49, 49)
    output = m(input)
    print(output.shape)

SK

ShuffleAttention

S2Attention

ParNetAttention

CoordAttention

MHSA

A2Attention

GCAttention

EffectiveSE

GEAttention

CrissCrossAttention

Polarized Self-Attention

Sequential Self-Attention

GAM

Biformer

EMA

CloAttention

LSKBlock

ECA

全称：Efficient Channel Attention

背景提要：更复杂的注意力模块不可避免地增加了模型的复杂性。通过剖析 SENet 中的通道注意力模块，我们凭经验证明避免降维对于学习通道注意力非常重要，适当的跨通道交互可以保持性能，同时显着降低模型复杂性。因此，我们提出了一种无需降维的局部跨通道交互策略，可以通过一维卷积有效地实现。此外，我们开发了一种自适应选择一维卷积核大小的方法，确定局部跨通道交互的覆盖范围。

1、主要思想：使用 $1\ast 1\ast k$ 的卷积代替 SE 注意力机制中的全连接和降维操作，将全连接变成卷积操作，减少了计算量。并提出了 自适应 k 值的选取策略，通过考虑每个通道及其 k 个邻居来捕获局部跨通道交互。

图示如下：

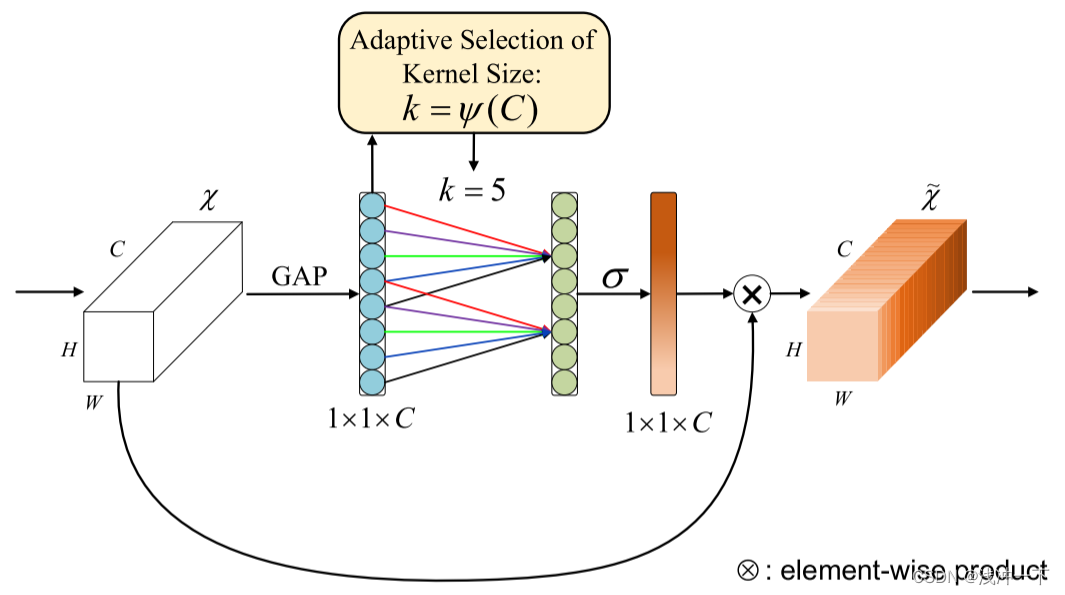
思想步骤解释：
第一步：作者从 SE 出发，说明避免降维。

SE模块的通道注意力通过下式计算：
ω = σ ( f { w 1 , w 2 } ( g ( X ) ) ) , \omega = \sigma(f_{\{w_1, w_2\}}(g(X))), ω=σ(f{w1​,w2​}​(g(X))),
其中， $g(x)=\frac{1}{WH}{\sum }_{i=1,j=1}^{W,H}{X}_{i,j}$ 为全局平均池化。如果 $y=g(x)$， 则 f { w 1 , w 2 } ( y ) f_{\{w_1, w_2\}}(y) f{w1​,w2​}​(y) 可以表示为 f { w 1 , w 2 } ( y ) = W 2 R e L U ( W 1 y ) f_{\{w_1, w_2\}}(y) = W_2ReLU(W_1y) f{w1​,w2​}​(y)=W2​ReLU(W1​y)，也就是两层全连接。$W_1$ 的尺度为 $R^{C\ast C/r}$，$W_2$ 的尺度为 $R^{C/r\ast C}$

作者阐述重新说明 SE 的原理，主要想给出下面的观点：$C/r$ 使得维数降低。 可以降低模型复杂度，但它破坏了通道与其权重之间的直接对应关系。例如，单个 FC 层使用所有通道的线性组合来预测每个通道的权重。但是 SE 中两层全连接首先将通道特征投影到低维空间，然后将其映射回来，使得通道与其权重之间的对应关系是间接的(没有一一对应)。

为了说明 SE 中通道与其权重之间的对应关系是间接的。为了验证效果，论文中将原始 SE 块与其三个变体（即 SE-Var1、SE-Var2 和 SE-Var3）进行比较，所有变体均不执行降维。比较结果如下：

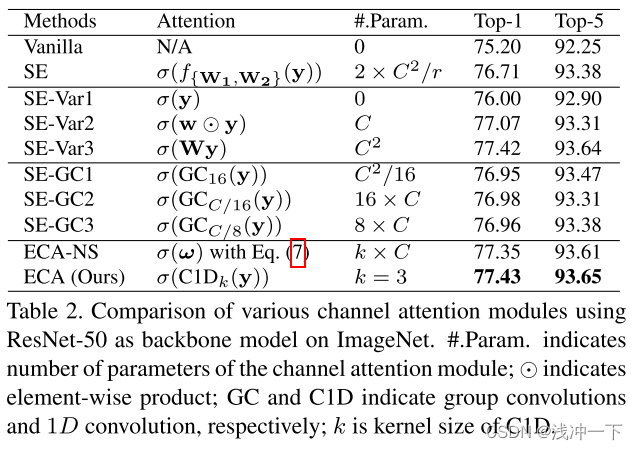
可以从实验对比上看得出，无参数的SE-Var1仍然优于原始网络，表明通道注意力有能力提高深度CNN的性能。同时，SE-Var2独立学习每个通道的权重，在涉及的参数较少的情况下略优于SE块。这可能表明通道及其权重需要直接对应，同时避免降维比考虑非线性通道依赖性更重要。此外，采用单个 FC 层的 SEVar3 的性能优于在 SE 块中进行降维的两个 FC 层。所有上述结果都清楚地表明，避免降维有助于学习有效的通道注意力。因此，我们开发了没有通道降维的 ECA 模块。

==>>> 所以通道降维不行

第二步：局部跨通道交互的方法

给定没有降维的聚合特征 $y\in R^C$，通道注意力可以通过以下方式学习：
$$\omega =\sigma (Wy)$$
其中，$W$ 是 $C\ast C$ 的参数矩阵，在 SE-Var2 和 SE-Var3 中， $W$ 矩阵的形式如下：(SE-Var2 为 1 对 1 全连接，SE-Var3 为 C 对 1 的全连接)
$$\mathbf{W}=\{\begin{array}{c}{\mathbf{W}}_{\text{var }2}=\left[\begin{array}{ccc}{w}^{1,1}& \dots & 0\\ ⋮& \ddots & ⋮\\ 0& \dots & w^{C,C}\end{array}\right]\\ {\mathbf{W}}_{\text{var }3}=\left[\begin{array}{ccc}{w}^{1,1}& \dots & w^{1,C}\\ ⋮& \ddots & ⋮\\ w^{1,C}& \dots & w^{C,C}\end{array}\right]\end{array}$$
其中 SE-Var2 的 $W_{var2}$ 是对角矩阵，涉及C个参数； SE-Var3 的 $W_{var3}$ 是一个全矩阵，涉及 C×C 参数。如方程式所示。主要区别在于SE-Var3考虑了跨渠道交互，而SEVar2则没有，因此SE-Var3取得了更好的性能。这一结果表明跨渠道交互有利于学习渠道注意力。然而，SEVar3 需要大量参数，导致模型复杂度较高，特别是对于大通道数。

所以作者想折中两种方式：SE-Var2 和 SE-Var3 之间可能的折衷方案是将 $W_{var2}$ 扩展到块对角矩阵，即
$${\mathbf{W}}_G=\left[\begin{array}{ccc}{\mathbf{W}}_G^1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\mathbf{W}}_G^G\end{array}\right]$$
是将通道分为$G$组，每个组包括$C/G$通道，并独立学习每个组中的通道注意力，以局部方式捕获跨通道交互。相应地，涉及到$C^2/G$参数。从卷积的角度来看，SE-Var2、SEVar3和上诉方式可以分别视为深度可分离卷积、FC层和组卷积。这里，具有组卷积的 SE 块（SE-GC）由 $\sigma (G{C}_G(y))=\sigma (W_{G}y)$ 表示。然而，过多的组卷积会增加内存访问成本，从而降低计算效率。

此外，如实验对比表所示，具有不同组的 SE-GC 没有比 SE-Var2 带来任何增益，这表明它不是捕获本地跨通道交互的有效方案。原因可能是SE-GC完全抛弃了不同群体之间的依赖关系。

==>>> 所以组卷积不行。

结合上面的说明：作者采用带状矩阵 $W_k$ 来学习通道注意力，$W_k$ 形式如下：
$$\left[\begin{array}{cccccccc}{w}^{1,1}& \cdots & w^{1,k}& 0& 0& \cdots & \cdots & 0\\ 0& w^{2,2}& \cdots & w^{2,k+1}& 0& \cdots & \cdots & 0\\ ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& \cdots & 0& 0& \cdots & w^{C,C-k+1}& \cdots & w^{C,C}\end{array}\right]$$
第一：避免了组卷积之间的完全独立。
第二：参数比较小。
第三：移动的考虑多个通道之间的关系。

具体公式如：$${\omega }_i=\sigma \left(\sum _{j=1}^k{w}_i^j{y}_i^j\right),y_i^j\in {\Omega }_i^k$$
其中， ${\Omega }_i^k$ 表示 $y_i$ 的 $k$ 个相邻通道的集合。

更有效的方法是让所有通道共享相同的学习参数，即：
$${\omega }_i=\sigma \left(\sum _{j=1}^k{w}^j{y}_i^j\right),y_i^j\in {\Omega }_i^k$$
请注意，这种策略可以通过内核大小为 k 的快速一维卷积轻松实现，即:
$$\omega =\sigma ({C1D}_k(\mathbf{y})),$$
其中 $C1D$ 表示一维卷积，仅涉及k个参数。实验证明，我们的 k = 3 的 ECA 模块实现了与 SE-var3 类似的结果，同时模型复杂度低得多，通过适当捕获本地跨渠道交互来保证效率和有效性。

第三步，确定 k 如何选取：局部跨通道交互覆盖
上述ECA模块旨在适当捕获局部跨道信息交互，因此需要确定通道交互信息的大致范围（即1D卷积的卷积核大小k）。虽然可以针对各种CNN架构中具有不同通道数的卷积块进行手动优化设置信息交互的最佳范围，但是通过手动进行交叉验证调整将花费大量计算资源。而且分组卷积已成功地用于改善CNN架构，在固定group数量的情况下，高维（低维）通道与长距离（短距离）卷积成正比。同理，跨通道信息交互作用的覆盖范围（即一维卷积的内核大小k）与通道维数C应该也是成正比的。换句话说，在k和C之间可能存在映射 $\varphi$：
$$C=\varphi (k).$$
最简单的映射是线性函数，即 $\varphi (k)=\gamma \ast k-b$。然而，以线性函数为特征的关系过于有限。另一方面，众所周知，通道维度 C（即滤波器的数量）通常设置为 2 的幂。因此，我们通过扩展线性函数 $\varphi (k)=\gamma \ast k-b$ 来引入一种可能的解决方案为非线性的，即
$$C=\varphi (k)=2^{(\gamma \ast k-b)},$$
所以，给定通道维度 C，内核大小 k 可以自适应地确定为
$$k=\psi (C)={\left|\frac{lo{g}_2(C)}{\gamma }+\frac{b}{\gamma }\right|}_{odd},$$
其中 $|t{|}_{odd}$ 表示 t 最接近的奇数。在本文中，我们在所有实验中将 $\gamma$ 和 $b$ 分别设置为 2 和 1。显然，通过映射 $\psi$，高维通道具有较长范围的相互作用，而低维通道通过使用非线性映射进行较短范围的相互作用。

2、模块使用地方：ECA模块是一个即插即用的模块，可以在卷积模块之后直接插入ECA模块，也可以在残差结构里面添加了ECA模块。

3、代码

import numpy as np
import torch
from torch import nn
from torch.nn import init
from collections import OrderedDict


class ECAAttention(nn.Module):

    def __init__(self, kernel_size=3):
        super().__init__()
        self.gap = nn.AdaptiveAvgPool2d(1)
        self.conv = nn.Conv1d(1, 1, kernel_size=kernel_size, padding=(kernel_size - 1) // 2)
        self.sigmoid = nn.Sigmoid()
        
    def init_weights(self):
        for m in self.modules():
            if isinstance(m, nn.Conv2d):
                init.kaiming_normal_(m.weight, mode='fan_out')
                if m.bias is not None:
                    init.constant_(m.bias, 0)
            elif isinstance(m, nn.BatchNorm2d):
                init.constant_(m.weight, 1)
                init.constant_(m.bias, 0)
            elif isinstance(m, nn.Linear):
                init.normal_(m.weight, std=0.001)
                if m.bias is not None:
                    init.constant_(m.bias, 0)

    def forward(self, x):
        y = self.gap(x)  # bs,c,1,1
        y = y.squeeze(-1).permute(0, 2, 1)  # bs,1,c
        y = self.conv(y)  # bs,1,c
        y = self.sigmoid(y)  # bs,1,c
        y = y.permute(0, 2, 1).unsqueeze(-1)  # bs,c,1,1
        return x * y.expand_as(x)


if __name__ == '__main__':
    input = torch.randn(50, 512, 7, 7)
    eca = ECAAttention(kernel_size=3)
    output = eca(input)
    print(output.shape)

SimAM

全称： Simple, Parameter-Free Attention Module

背景提要：现有的注意力模块通常被继承到每个块中，以改进来自先前层的输出。这种细化步骤通常沿着通道维度(a)或空间维度(b)操作,这些方法生成一维或二维权重，并平等对待每个通道或空间位置中的神经元，
  通道注意力：1D注意力，它对不同通道区别对待，对所有位置同等对待；
  空域注意力：2D注意力，它对不同位置区别对待，对所有通道同等对待。
这可能会限制他们学习更多辨别线索的能力。因此三维权重(本文)优于传统的一维和二维权重注意力

1、主要思想：基于一些著名的神经科学理论，提出优化能量函数来找出每个神经元的重要性(三维权重)。

思想步骤解释：
  为更好的实现注意力，我们需要评估每个神经元的重要性。在神经科学中，信息丰富的神经元通常表现出与周围神经元不同的放电模式。而且，激活神经元通常会抑制周围神经元，即空域抑制。换句话说，具有空域抑制效应的神经元应当赋予更高的重要性，找到这些神经元最简单的实现：测量一个目标神经元和其他神经元之间的线性可分性。

如何理解这个线性可分性：如果当前神经元和其他神经元差异性很明显的话，通过一层 $y=wx+b$的分类器，我们能够很容易的将其区分开，结果的均值和方差就很小。要是差异不大，很难分开，那结果的均值和方差就比较大。

基于这些神经科学发现，作者为每个神经元定义了以下能量函数:
$$\begin{array}{r}{e}_t\left(w_t,b_t,\mathbf{y},x_i\right)={\left(y_t-\hat{t}\right)}^2+\frac{1}{M-1}\sum _{i=1}^{M-1}{\left(y_o-{\hat{x}}_i\right)}^2\end{array}$$
其中：$\hat{t}=w_{t}t+b_t$ 和 ${\hat{x}}_i=w_t{x}_i+b_t$ 是 $t$ 和 $x_i$ 的线性变换，其中 $t$ 和 $x_i$ 是输入特征 $X\in R^{C\times H\times W}$ 的单个通道中的目标神经元和其他神经元。$i$ 是空间维度上的索引，$M=H\times W$ 是该通道上的神经元数量。 $w_t$ 和 $b_t$ 是变换的权重和偏置，我们想要求解的就是 $w_t$ 和 $b_t$。
方程(1)中的所有值都是标量。当 $\hat{t}$ 等于 $y_t$ 且所有其他 ${\hat{x}}_i$ 均为 $y_o$ 时，方程（1）达到最小值，其中 $y_t$ 和 $y_o$ 是两个不同的值。

通过最小化方程，方程(1)相当于找到目标神经元 t 与同一通道中所有其他神经元之间的线性可分离性。为了简单起见，我们对 $y_t$ 和 $y_o$ 采用二进制标签（即 1 和 -1），并在方程（1）中添加权重正则化器。最终的能量函数由下式给出：
$$\begin{array}{rlr}{e}_t\left(w_t,b_t,\mathbf{y},x_i\right)& =\frac{1}{M-1}\sum _{i=1}^{M-1}{\left(-1-\left(w_t{x}_i+b_t\right)\right)}^2& +{\left(1-\left(w_{t}t+b_t\right)\right)}^2+\lambda w_t^2\end{array}$$

理论上，每个通道都有 M 个能量函数 (每个神经元一个)。通过 SGD 等迭代求解器求解所有这些方程的计算量非常大。幸运的是，方程(2)对于 $w_t$ 和 $b_t$ 有一个快速闭式解，可以通过以下方式轻松获得：
$$\begin{array}{r}{w}_t=-\frac{2(t-{\mu }_t)}{(t-{\mu }_t{)}^2+2{\sigma }_t^2+2\lambda },\\ b_t=-\frac{1}{2}(t+{\mu }_t)w_t.\end{array}$$
其中：${\mu }_t=\frac{1}{M-1}{\sum }_{i=1}^{M-1}{x}_i$ 和 ${\sigma }_t^2=\frac{1}{M-1}{\sum }_i^{M-1}(x_i-{\mu }_t{)}^2$ 是对该通道中除 t 之外的所有神经元计算的平均值和方差。

由于方程（3）和方程（4）所示的现有解是在单个通道上获得的，因此可以合理地假设单个通道中的所有像素遵循相同的分布(均值和方差一样)。考虑到这一假设，可以计算所有神经元的平均值和方差，并为该通道上的所有神经元重复使用。它可以显着降低计算成本，避免迭代计算每个位置的 $\mu$ 和 $\sigma$。
因此，最小能量可以通过以下公式计算：
$$\begin{array}{r}{e}_t^{\ast }=\frac{4\left({\hat{\sigma }}^2+\lambda \right)}{(t-\hat{\mu }{)}^2+2{\hat{\sigma }}^2+2\lambda },\end{array}$$
其中：$\hat{\mu }=\frac{1}{M}{\sum }_{i=1}^M{x}_i$ 和 ${\hat{\sigma }}^2=\frac{1}{M}{\sum }_i^M(x_i-\hat{\mu }{)}^2$ 是该通道所有神经元的平均值和方差。

公式(5)表明能量 $e_t^{\ast }$ 越低，神经元 $t$ 与周围神经元的区别越明显，对视觉处理越重要。因此，每个神经元的重要性可以通过 $1/e_t^{\ast }$ 得到。

哺乳动物大脑中的注意力调节通常表现为对神经元反应的增益（即缩放）效应。因此，我们使用缩放运算符而不是加法来进行特征细化。我们模块的整个细化阶段是：
$$\begin{array}{r}\hat{X}=sigmoid(\frac{1}{E})\odot X=\sigma (\frac{(t-\hat{\mu }{)}^2+2{\hat{\sigma }}^2+2\lambda }{4\left({\hat{\sigma }}^2+\lambda \right)})\odot X\\ =\sigma (\frac{(t-\hat{\mu }{)}^2}{4\left({\hat{\sigma }}^2+\lambda \right)}+0.5)\odot X\end{array}$$
其中: $E$ 将所有 $e_t^{\ast }$ 跨通道和空间维度进行分组。添加 $sigmoid$ 是为了限制 $E$ 值过大，不会影响每个神经元的相对重要性，因为 $sigmoid$ 是单峰函数。

论文给出的代码流程图如下：

值得注意的是：论文中唯一的超参数 $\lambda$ 在实验的时候为 $1e-4$。

2、模块使用地方：一个即插即用的模块，可以在卷积模块之后直接插入simAM模块。

3、代码

import torch
import torch.nn as nn


class SimAM(torch.nn.Module):
    def __init__(self, e_lambda=1e-4):
        super(SimAM, self).__init__()

        self.activaton = nn.Sigmoid()
        self.e_lambda = e_lambda

    def __repr__(self):
        s = self.__class__.__name__ + '('
        s += ('lambda=%f)' % self.e_lambda)
        return s

    @staticmethod
    def get_module_name():
        return "simam"

    def forward(self, x):
        b, c, h, w = x.size()
        n = w * h - 1
        # 计算(t-u)^2
        x_minus_mu_square = (x - x.mean(dim=[2, 3], keepdim=True)).pow(2)
        y = x_minus_mu_square / (4 * (x_minus_mu_square.sum(dim=[2, 3], keepdim=True) / n + self.e_lambda)) + 0.5

        return x * self.activaton(y)


if __name__ == '__main__':
    input = torch.randn(3, 64, 7, 7)
    model = SimAM()
    print(model)
    outputs = model(input)
    print(outputs.shape)

TripletAttention

SGE

全称：

背景提要：

1、主要思想：

简单图示如下：

思想步骤解释：

值得注意的是：

2、模块使用地方：

3、代码

import torch