关于此题的我的往期文章：

leetCode 70.爬楼梯 动态规划_呵呵哒(￣▽￣)"的博客-CSDN博客https://blog.csdn.net/weixin_41987016/article/details/133325224?spm=1001.2014.3001.5501

• 上i-1层楼梯，有 dfs(i-1) 种方法，那么再一步跳一个台阶就是 dfs(i) 了
• 上i-2层楼梯，有 dfs(i-2) 种方法，那么再一步跳两个台阶就是 dfs(i) 了

也就是说可以求出 dfs(i)，即 dfs(i) = dfs(i-1) + dfs(i-2)

（1） 递归（超时）

class Solution {
public:
    // 递归
    int climbStairs(int n) {
        function<int(int)> dfs=[&](int i) -> int {
            if(i==0 || i==1) return 1;
            return dfs(i-1) + dfs(i-2);
        };
        return dfs(n);
    }
};

（2）递归搜索 + 保存计算结果 = 记忆化搜索

class Solution {
public:
    // 记忆化搜索
    int climbStairs(int n) {
        vector<int> memo(n+2,-1);
        function<int(int)> dfs=[&](int i) -> int {
            if(i==0 || i==1) return 1;
            int &res = memo[i];
            if(res != -1) return res;
            return res=dfs(i-1) + dfs(i-2);
        };
        return dfs(n);
    }
};

（3）1:1 翻译成递推

• 

• 

• 

class Solution {
public:
    // 递推
    int climbStairs(int n) {
        vector<int> f(n+2,0);
        f[0]=1;
        f[1]=1;
        for(int i=0;i<=n-2;i++) 
            f[i+2] = f[i+1] + f[i];
        return f[n];
    }
};

class Solution {
public:
    // 递推
    int climbStairs(int n) {
        vector<long> f(n+1,0);
        f[0]=1;
        f[1]=1;
        for(int i=2;i<=n;i++) 
            f[i] = f[i-1] + f[i-2];
        return f[n];
    }
};

• 空间优化

class Solution {
public:
    // 递推
    int climbStairs(int n) {
        int f0=1,f1=1,sum;
        for(int i=2;i<=n;i++) {
            sum = f0+f1;
            f0 = f1;
            f1=sum;
        }  
        return f1;
    }
};

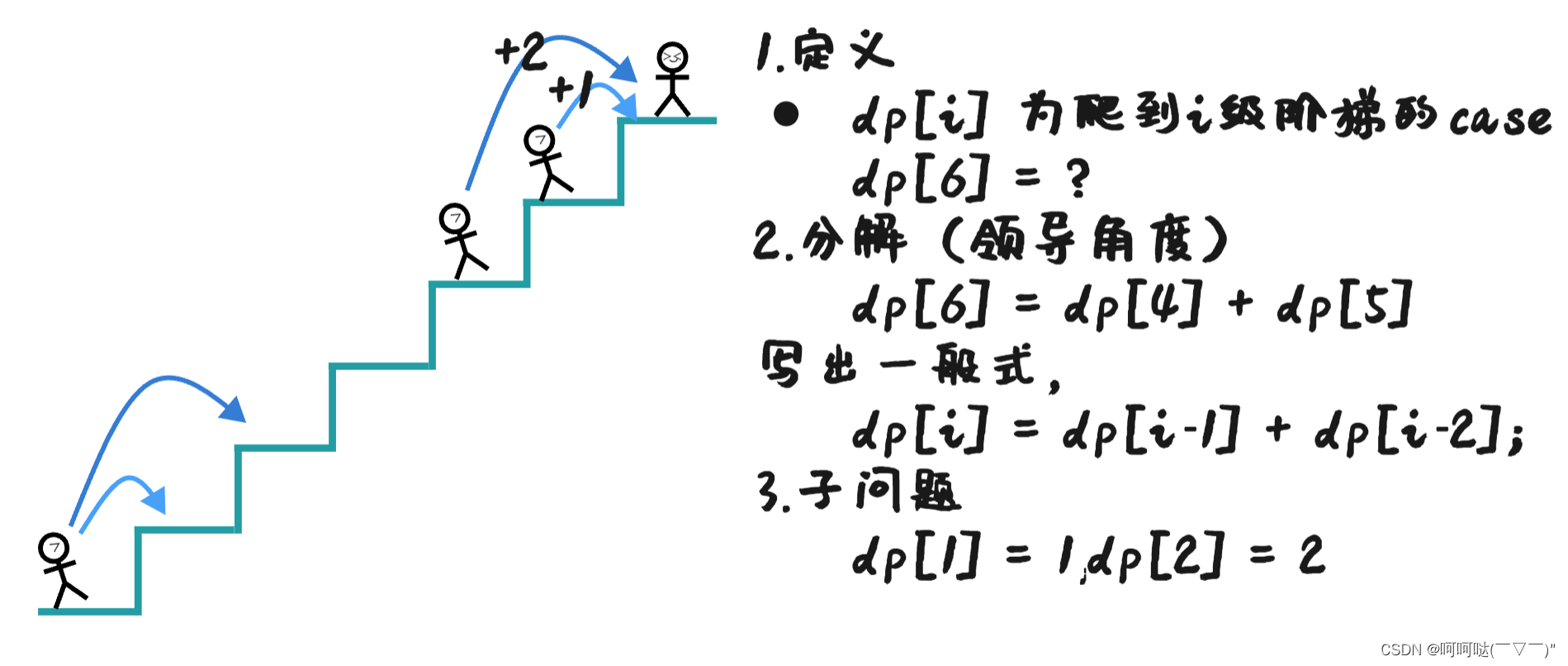
（4）动态规划

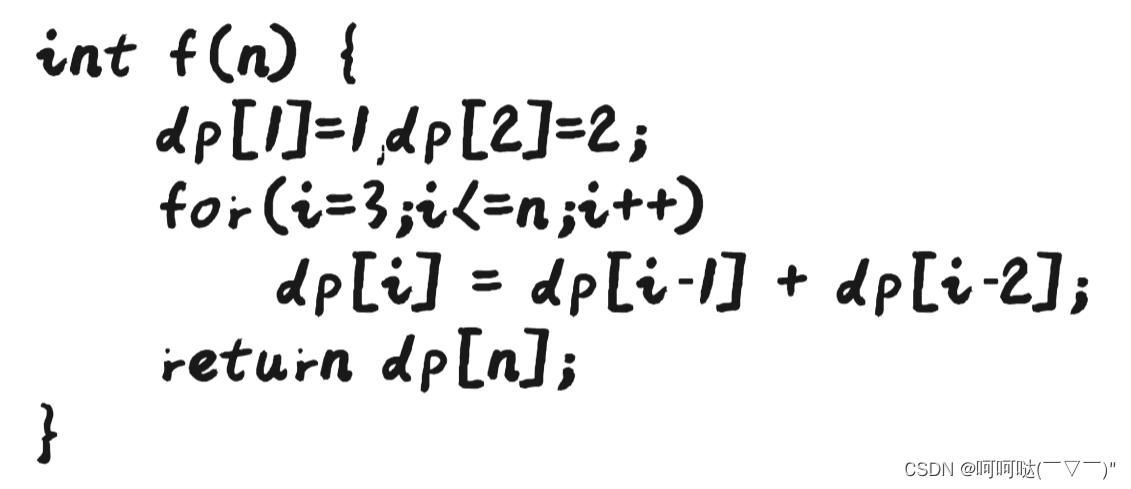
class Solution {
public:
int climbStairs(int n) {
        if(n<=1) return n;// 因为下面直接对dp[2] 操作了，防止空指针
        vector<int> dp(n+1,0);
        dp[1]=1;
        dp[2]=2;
        for(int i=3;i<=n;i++) 
            dp[i] = dp[i-1] + dp[i-2];
        return dp[n];
    }
};