本文紧接前文：

《python基于不同方法实现特征工程常用的归一化技术Normalization对比分析》

前文主要是讲解对于数值型特征数据在特征工程或者是数据处理阶段往往需要用到数据尺度归一化操作，基于原生的对象和numpy第三方库分别实现了按列归一化计算和整体归一化计算，基于真实的数据进行对比分析，验证两种方法的正确性。

本文主要是针对图像数据来进行归一化处理。

这里主要实现了三种项目中常用的操作。

第一种：

直接除以255.0实现原始图像的缩放处理

第二种：

跟前文同样的基础原理，基于min-max实现归一化操作计算

第三种：

基于zero-mean实现归一化操作计算，将原始图像数据分布转化为正态分布形态

至于具体的原理这里就不再赘述了，感兴趣话可以直接查对应的资料即可，这里直接看代码实现，如下所示：

def channelTranspose(tensor):
    """
    图像通道调整
    """
    img_arr = np.array(tensor)
    img_tr = img_arr.transpose(1, 2, 0)
    return img_tr




def imgNormalization(pic="test.jpg"):
    """
    图像归一化
    """
    img = Image.open(pic)
    transform = transforms.Compose([transforms.ToTensor()])
    img_tensor = transform(img)
    mean, std = img_tensor.mean([1, 2]), img_tensor.std([1, 2])
    transform_norm = transforms.Compose(
        [transforms.ToTensor(), transforms.Normalize(mean, std)]
    )
    img_normalized = transform_norm(img)
    img_np = np.array(img)
    print(img_np.shape)
    simple = img_np / 255.0
    print("mean and std before normalize:")
    print("Mean of the image:", mean)
    print("Std of the image:", std)
    result1 = channelTranspose(img_tensor)
    result2 = channelTranspose(img_normalized)
    # 可视化对比
    imgs_list = [img_np, simple, result1, result2]
    titles = ["orignal", "simple", "min-max normalization", "zero-mean normalization"]
    figsize = (20, 16)
    _, axes = plt.subplots(2, 2, figsize=figsize)
    axes = axes.flatten()
    for i, (ax, img) in enumerate(zip(axes, imgs_list)):
        try:
            img = np.array(img)
        except:
            pass
        ax.imshow(img)
        ax.axes.get_xaxis().set_visible(False)
        ax.axes.get_yaxis().set_visible(False)
        if titles:
            ax.set_title(titles[i])
    plt.savefig(save_path)

测试图像如下：

 结果图像如下所示：

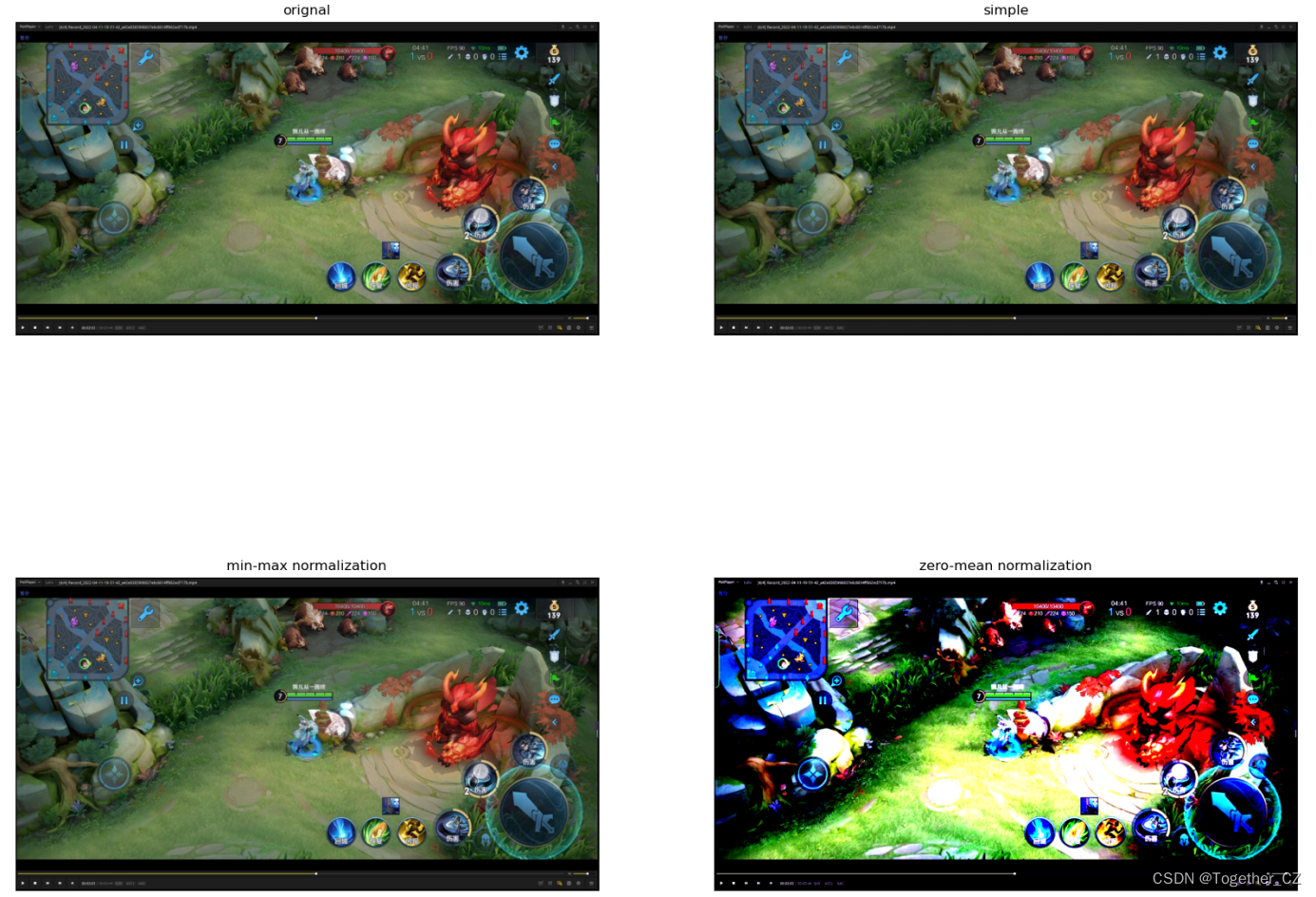
 从直观效果上来看：不难分析出来simple方法和min-max方法得到的结果应该是大致相同甚至是完全相同的，这个从min-max的计算公式上面就可以窥探出来。

为了进一步验证猜想，这里对其每种方法计算处理后得到的图像像素分布直方图进行了可视化对比分析展示，直方图的粒度可以自由调整，我这里由粗到细分别展示不同方法处理后的对比可视化结果，如下所示：

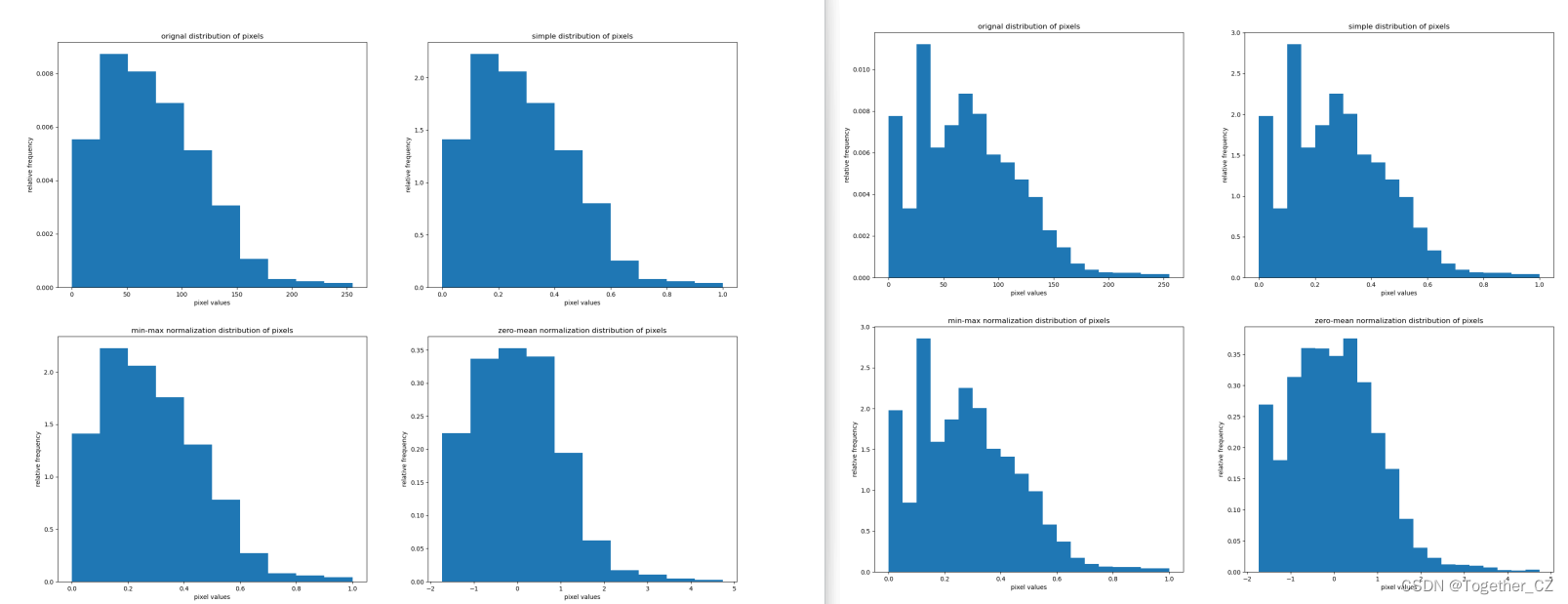
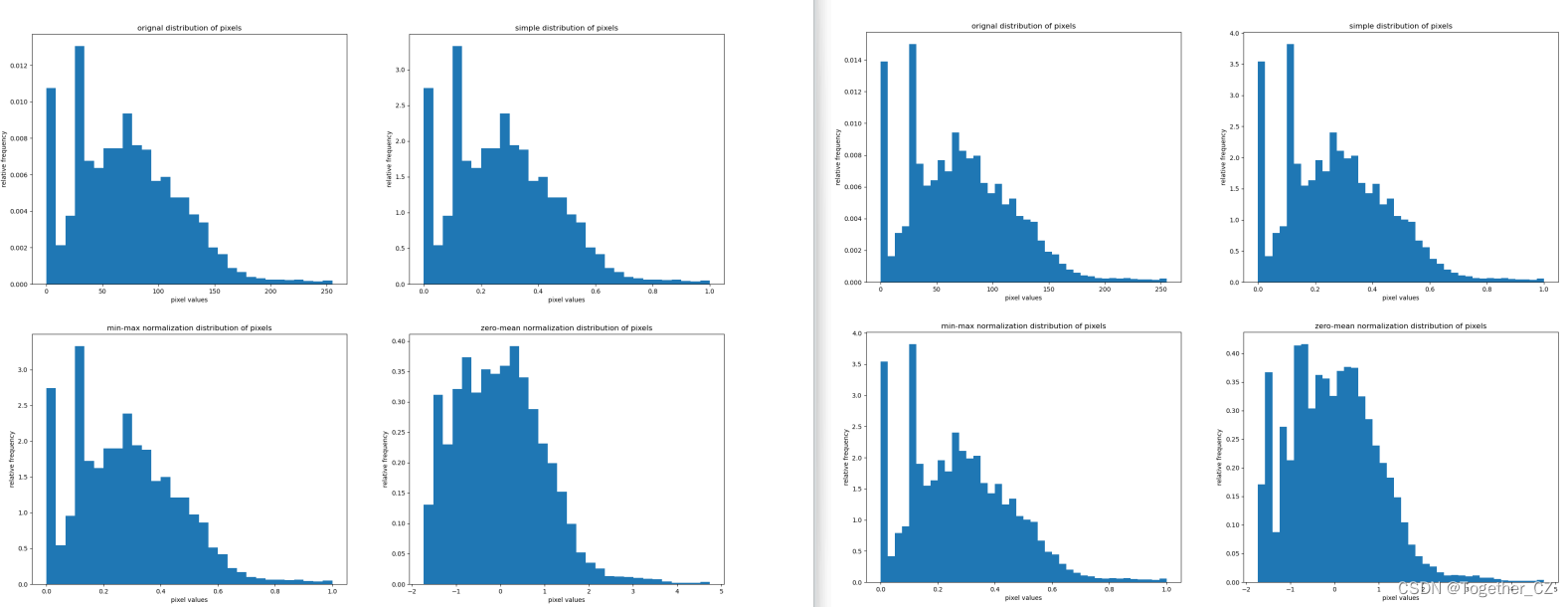
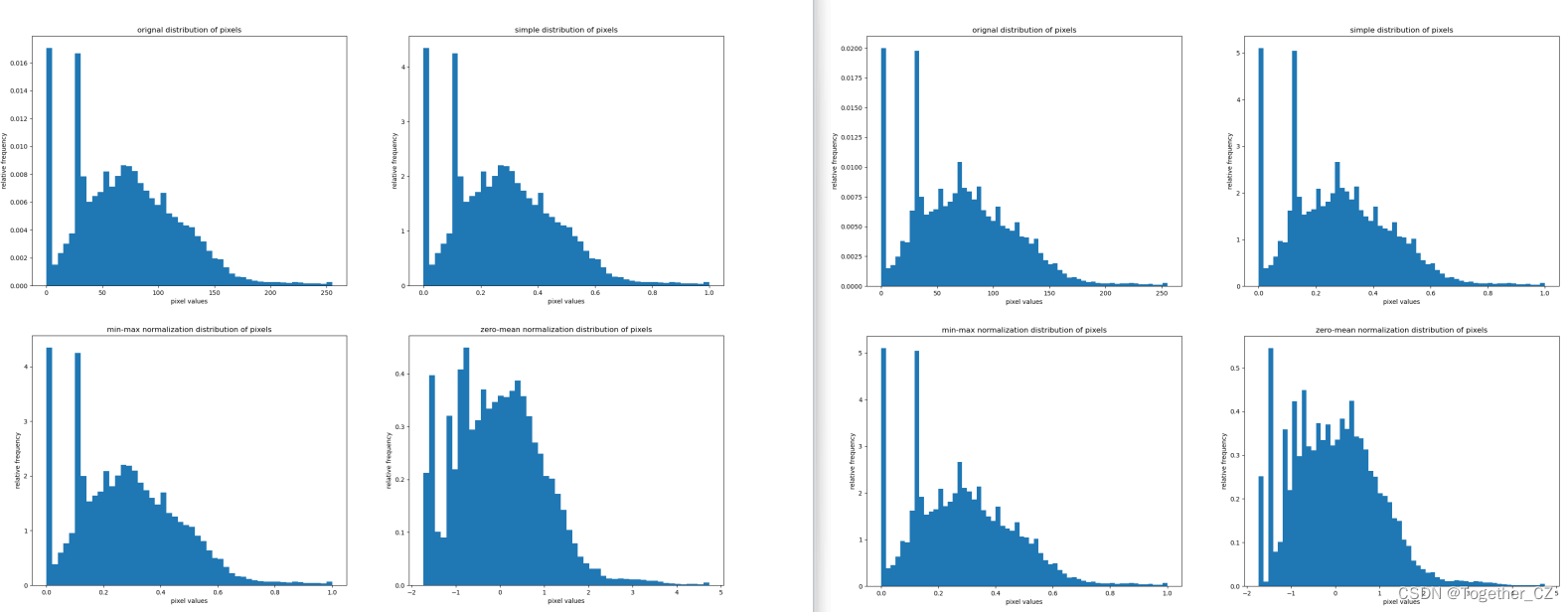
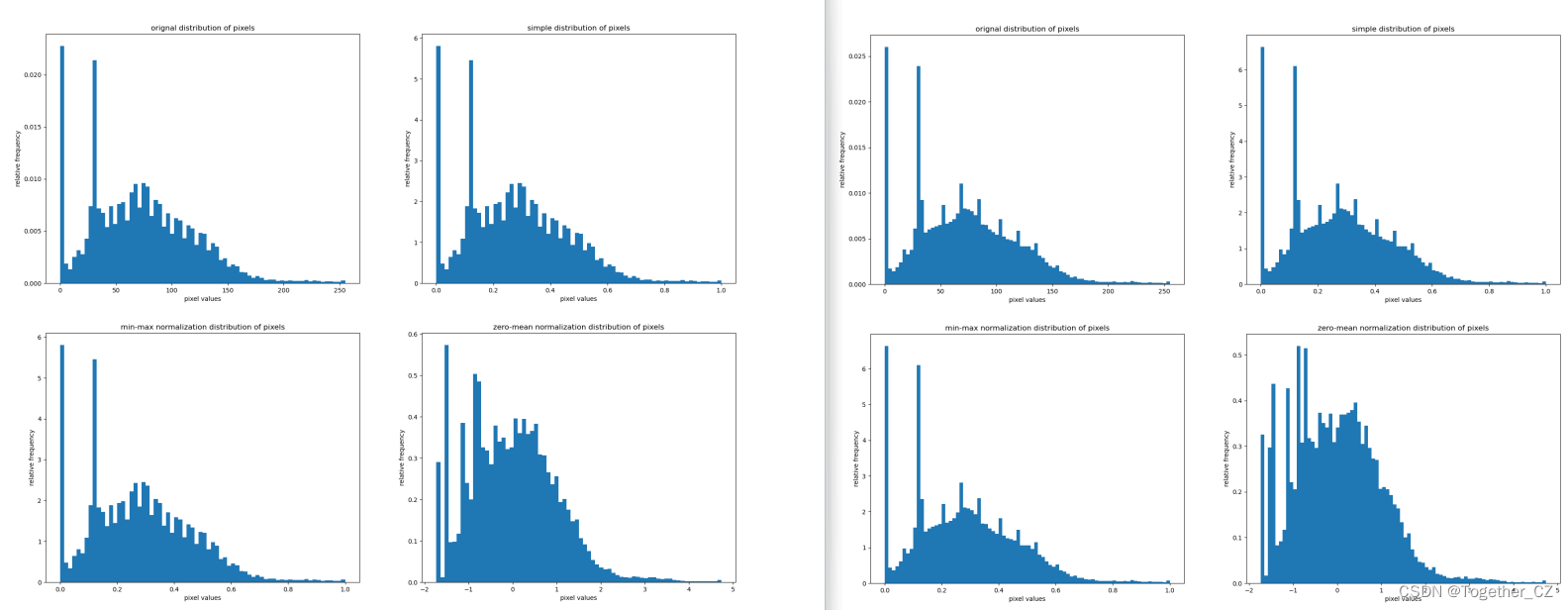
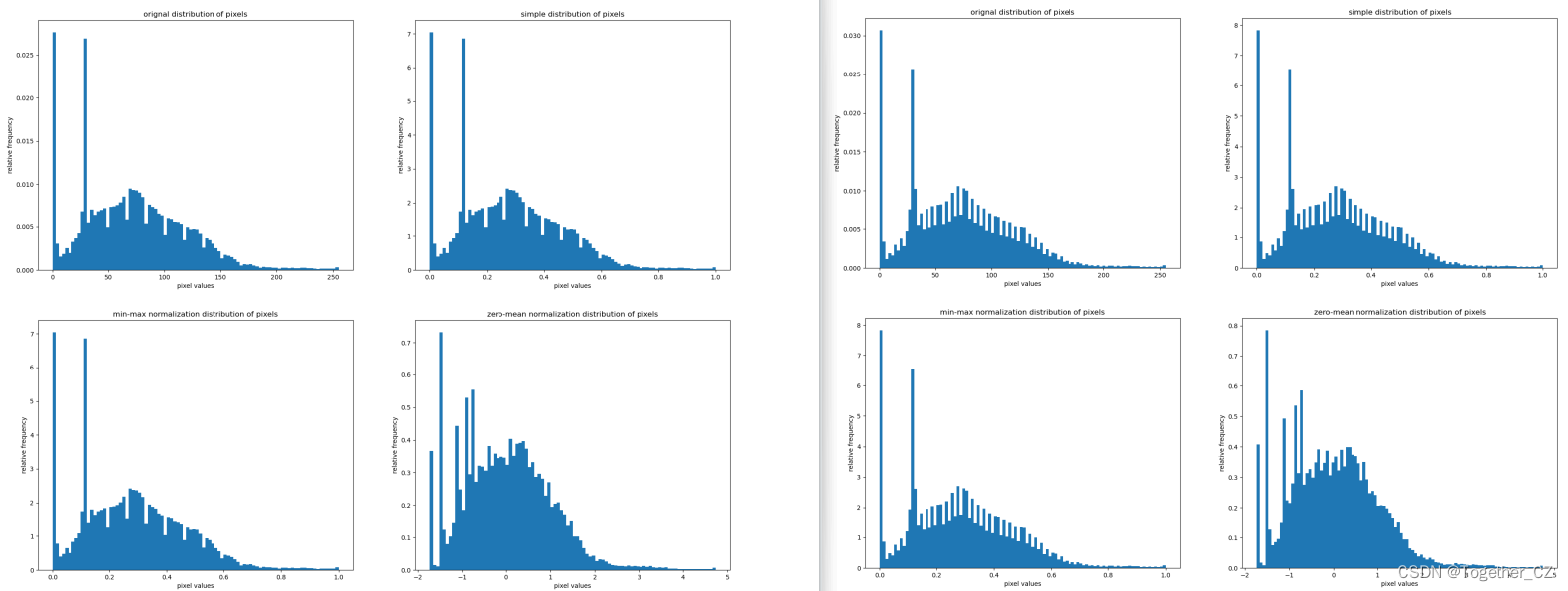
 经此可视化过程直观展示能够非常细致地看出来三种不同的处理方法存在的差异性了。

感兴趣的话可以自行实践，记录备忘！