1739. 放置盒子

题目描述

有一个立方体房间，其长度、宽度和高度都等于 n 个单位。请你在房间里放置 n 个盒子，每个盒子都是一个单位边长的立方体。放置规则如下：

你可以把盒子放在地板上的任何地方。
如果盒子 x 需要放置在盒子 y 的顶部，那么盒子 y 竖直的四个侧面都必须与另一个盒子或墙相邻。

给你一个整数 n ，返回接触地面的盒子的最少可能数量。

示例 1

输入：n = 3
输出：3
解释：上图是 3 个盒子的摆放位置。
这些盒子放在房间的一角，对应左侧位置。
在这里插入图片描述

示例 2

输入：n = 4
输出：3
解释：上图是 3 个盒子的摆放位置。
这些盒子放在房间的一角，对应左侧位置。
在这里插入图片描述

示例 3

输入：n = 10
输出：6
解释：上图是 10 个盒子的摆放位置。
这些盒子放在房间的一角，对应后方位置。
在这里插入图片描述

提示

1 <= n <= 10⁹

算法一：找规律 + 数学思想（等差数列求和）

思路

为了方便画图找规律，我们将立体图转换为平面图来表示：
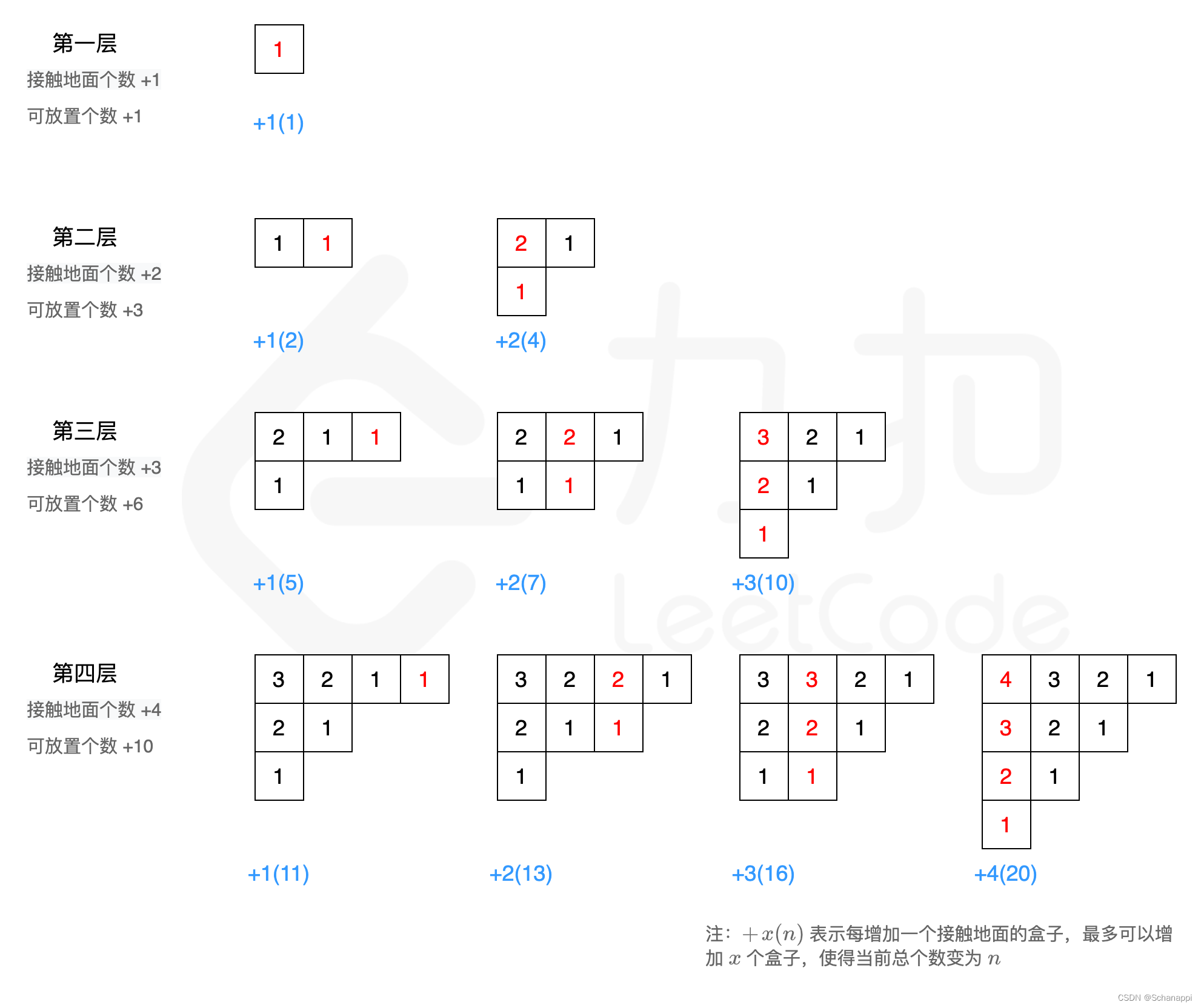
根据贪心思想，接触地面的盒子构成的总体形状应该是一个左上三角，这样才可以使得内部的盒子垒起来的高度更高，以保证接触地面盒子数量最小的情况下容纳更多的盒子。我们画出前四层的盒子增长情况，来试探一下有什么规律存在：
从上图不难发现，第 i 层最多可以增加 i 个接触地面的盒子。对于第 i 层而言，此时总的接触地面的盒子数为：1+2+3+...+i = i*(i+1)/2 。

第 i 层对应的上限为：1+2+3+...+i = i*(i+1)/2 ；
此时总的上限为：1+(1+2)+(1+2+3)+...+(1+2+3+...+i) = i*(i+1)*(i+2)/6。
要放置 n 个盒子，需要完整地放满第 i 层（达到第 i 层的上限），剩余的盒子放在第 i+1 层。
我们先考虑第 i 层（上限数）：

设 x 为满足 i*(i+1)*(i+2)/6 ≤ n 的最大 i，ans 代表总的接触地面的盒子数，max_n 代表总上限。

由于 max_n + ans + i 的值等于第 i+1 层上限数 -1 ，因此这个值可以作为循环结束的依据，可以确保当前层数 i 是最大值。
最后考虑剩余的盒子，此时已经放置的盒子数为第 i 层的上限，也就是max_n 。

对于第 i+1 层，如果接触地面的盒子增加 j 个，那么对应上限增加 1+2+...+j = j*(j+1)/2 。所以设 y 为满足 x(x+1)(x+2)/6 + j(j+1)/2 ≥ n 的最小 j。
最终答案就是 x(x+1)/2 + y 。

收获

通过这道题发现，通过找规律和数学思想解题之后，代码会变得简洁很多，因此不要一味地用代码暴力求解。

算法情况

时间复杂度：O（³√ n），通过计算可以发现，i 和 j 至多为 ³√ n
空间复杂度：O（1）

代码

class Solution {
public:
    int minimumBoxes(int n) {
        int ans = 0, max_n = 0;
        // max_n+ans+i:i+1层上限数-1
        // 能够保证此时i取到最大
        for (int i = 1; max_n+ans+i<= n; ++i) {
            ans += i;
            max_n += ans;
        }
        for (int j = 1; max_n < n; ++j) {
            ++ans;
            max_n += j;
        }
        return ans;
    }
};