今天讲二分的例题,一道是“砍树”,一道是“木材加工”
目录
题目:砍树
思路1:
思路2:
题目:木材加工
思路:
题目:砍树


思路1:
二分查找:对高度进行二分
二分依据:该高度下砍出的木材
#include<bits/stdc++.h> //砍树P1873 (二分查找) O(nlogn)
using namespace std;
long long n,bz,s=0,mid,l,r,trees[1000008];
int main()
{
scanf("%lld%lld",&n,&bz);
for(int i=1;i<=n;i++)
{
scanf("%lld",&trees[i]);
r=max(r,trees[i]);//找到最长木材
}
while(l<=r) //最右模板
{
mid=(l+r)/2; //从中间点开始作为伐木机高度
s=0;
for(int i=1;i<=n;i++)
if(trees[i]>mid) s+=trees[i]-mid; //计算这个高度下砍的木材
if(s<bz) //木材不足
r=mid-1;//减小高度增加木材
else
l=mid+1;//增加高度减小木材
}
cout<<r;
return 0;
}
思路2:
先进行排序(从高到低),砍第i棵树时,按照第i+1棵树高度砍,则获得的新高度为(h(i+1)-h(i))*i
(有点偏数学,不喜欢数学的小伙伴可以跳过了)
#include<cstdio> //砍树P1873 (贪心)(700毫秒)O(n)+O(n)*(logn)
#include<cstring>
#include<algorithm>
using namespace std;
int tree[1000001];
int n,m;
int main()
{
int i,num,ans;
long long sum=0;
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++) scanf("%d",&tree[i]);
sort(tree+1,tree+n+1); //默认按从低到高进行排序,那就倒着砍
num=n;
while(sum<m)
{
sum+=(tree[num]-tree[num-1])*(n-num+1);
num--;
}
ans=tree[num]+(sum-m)/(n-num); //因为并不是真正的把数砍了,所以最后的高度还需要算出来
printf("%d\n",ans);
return 0;
}
题目:木材加工

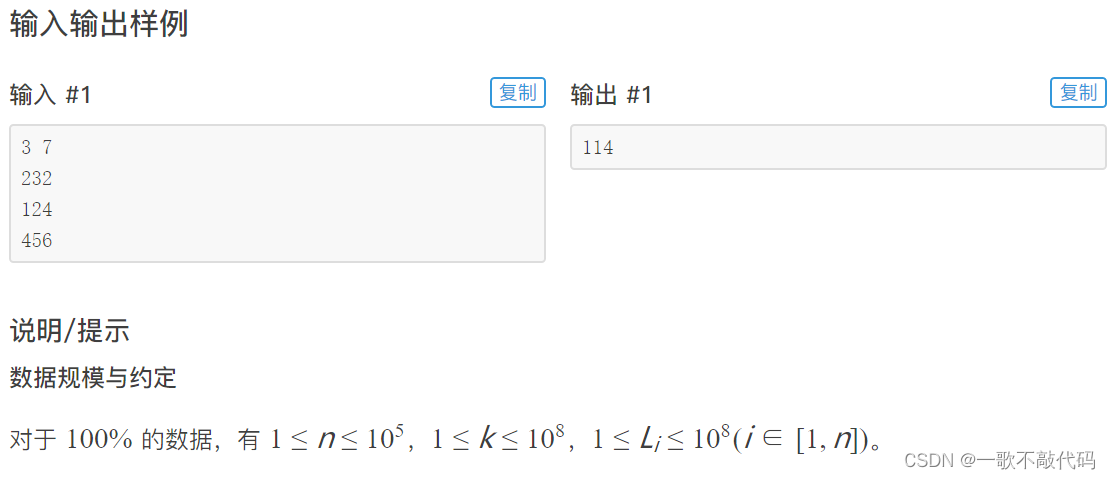
思路:
二分查找: 对最小段长度进行二分
二分依据: 该最小段下需要切的段数
#include <bits/stdc++.h> //P2440木材加工 (二分查找)
using namespace std;
long long n, k;
long long a[1000005];
bool f(long long x) {
long long ans = 0;
for (int i = 1; i <= n; i++) { //把每根木材按照x长度分成的段数相加
ans += a[i] / x;
}
return ans >= k; //发现分的段比k多
}
int main() {
cin >> n >> k;
for (int i = 1; i <= n; i++) cin >> a[i];
long long l = 0, r = 100000001; //答案所在的区间
long long mid;
while (l + 1 < r) { //开始二分
mid = (l + r) / 2;
if (f(mid)) l = mid; //如果mid分的过多说明mid太小了,所以向右压缩
else r = mid;
}
cout<<l<<endl; //输出重复的最后一个
// while(l<=r){ //或最右模板的
// mid =(l+r)/2;
// if(f(mid)) l=mid+1;
// else r=mid-1;
// }
// cout<<r;
return 0;
}