题目
96. 不同的二叉搜索树
中等
相关标签
树 二叉搜索树 数学 动态规划 二叉树
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
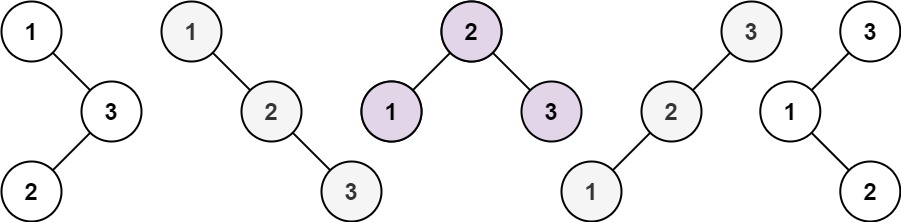
输入:n = 3 输出:5
示例 2:
输入:n = 1 输出:1
提示:
1 <= n <= 19
思路和解题方法 一 动态规划
vector<int> dp(n + 1);:创建一个名为dp的整数向量,长度为 n+1。dp[i]表示节点数量为 i 时的二叉搜索树数量。
dp[0] = 1;:将dp[0]初始化为 1,因为当节点数量为 0 时,只有一种情况,即空树。
for (int i = 1; i <= n; i++):遍历节点数量从 1 到 n 的所有情况。
for (int j = 1; j <= i; j++):对于当前节点数量 i,遍历 j 从 1 到 i 的所有情况,表示以 j 作为根节点的情况。
dp[i] += dp[j - 1] * dp[i - j];:计算以 j 作为根节点时,左子树和右子树的组合数,并将其累加到dp[i]中。dp[j - 1]表示左子树的组合数,dp[i - j]表示右子树的组合数。最终返回
dp[n],即节点数量为 n 时的二叉搜索树数量。
复杂度
时间复杂度:
O(n^2)
时间复杂度为 O(n^2),因为有两个嵌套的循环。
空间复杂度
O(n)
空间复杂度为 O(n),因为使用了一个长度为 n+1 的向量来保存中间结果。
c++ 代码一
class Solution {
public:
int numTrees(int n) {
// 创建一个长度为n+1的vector,用于存储不同数值的二叉搜索树的数量
vector<int> dp(n + 1);
// 初始化dp[0]为1,因为空二叉树也算一棵二叉树
dp[0] = 1;
// 循环计算dp数组中每个元素的值
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++) {
// 根据公式计算dp[i]的值,即左子树数量×右子树数量之和
dp[i] += dp[j - 1] * dp[i - j];
}
}
// 返回dp[n],即n个节点的不同数值的二叉搜索树的数量
return dp[n];
}
};
思路和解题方法 二 数学思维
代码中,使用了一个变量C来表示二叉搜索树的数量。初始时,将C设置为1。
然后通过循环遍历i从0到n-1的所有情况,进行如下操作:
将C乘以2 * (2 * i + 1)。这一步是为了计算当前节点数量为i+1时,左子树的组合数。因为左子树的节点数量比根节点小,所以乘以2 * (2 * i + 1)可以得到左子树的组合数。
将C除以(i + 2)。这一步是为了计算右子树的组合数。右子树的节点数量比根节点大,所以除以(i + 2)可以得到右子树的组合数。
通过每次循环更新C的值,最终得到的C即为n个节点的二叉搜索树的数量。
这段代码利用了组合数的性质,将计算二叉搜索树数量的问题转化为了求解组合数的问题。
通过不断更新C的值,可以高效地计算出给定节点数量的二叉搜索树的数量。
需要注意的是,由于C的值可能非常大,所以在返回结果之前,将C强制转换为int类型。
复杂度
时间复杂度:
O(n)
时间复杂度分析: 代码中的循环从0到n-1遍历,每次循环都执行一些基本的数学运算,包括乘法、除法和加法。这些运算的时间复杂度都是常数级别的。因此,整个循环的时间复杂度为O(n)。
空间复杂度
O(1)
空间复杂度分析: 代码中只使用了一个变量C来存储二叉搜索树的数量,而且在整个过程中不需要额外的数据结构来存储中间结果。因此,空间复杂度为O(1),即常数级别的空间消耗。
c++ 代码二
class Solution {
public:
int numTrees(int n) {
long long C = 1; // 初始化组合数C为1,用于存储二叉搜索树的数量
for (int i = 0; i < n; ++i) { // 循环计算每个节点数量的二叉搜索树的数量
C = C * 2 * (2 * i + 1) / (i + 2); // 计算组合数C的值
}
return (int)C; // 将组合数C强制转换为int类型并返回
}
};
觉得有用的话可以点点赞,支持一下。
如果愿意的话关注一下。会对你有更多的帮助。
每天都会不定时更新哦 >人< 。