一、哈夫曼树概念

        哈夫曼树又称最优树给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

         例给定一个有序数组{3,5,6,9,10}，构造出一个哈夫曼树如下：

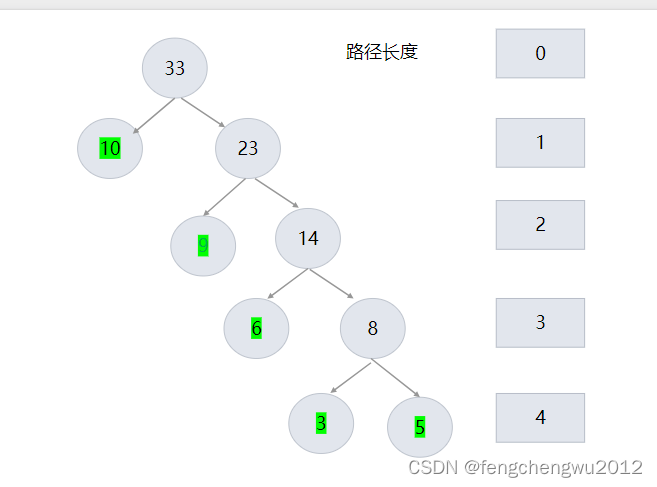
       树的带权路径长度规定为所有叶子结点的带权路径长度之和，记为WPL

        WPL = (3+5)*4 +  6*3 + 9*2 +10*1 = 98

二、实现代码

1、定义树结点

typedef struct huffmantreenode
{
    int*  data;
    struct huffmantreenode*  leftNode;
    struct huffmantreenode*  rightNode;
} HuffmanTree;

2、声明函数操作

/**
 *创建节点
*/
HuffmanTree*  create_huffman_tree(int data);

/**
 * 初始化哈夫曼根节点
*/
HuffmanTree*  create_huffman_tree_root(int first,int second);

/**
 * 新增节点
*/
void  insert_huffmantree_node(HuffmanTree** tree,int data);

/**
 * 前序遍历
*/
void  pre_oder_huffmantree(HuffmanTree** tree);

/**
 * 销毁树
*/
void  destroy_huffmantree(HuffmanTree* tree);

3、函数定义

HuffmanTree*  create_huffman_tree(int data)
{
    HuffmanTree* node = malloc(sizeof(HuffmanTree*));
    if(node==NULL)
    {
      perror("节点点申请内存失败");
      return NULL;
    }
   node->data = malloc(sizeof(int*));
   *(node->data) = data;
   node->leftNode = NULL;
   node->rightNode = NULL;
   return node;
}


HuffmanTree*  create_huffman_tree_root(int first,int second)
{
  HuffmanTree*  firstNode = create_huffman_tree(first);
  HuffmanTree*  secondNode = create_huffman_tree(second);
  HuffmanTree*  root = create_huffman_tree(first+second);
  root->leftNode  = firstNode;
  root->rightNode = secondNode;
  return root;
}


void  insert_huffmantree_node(HuffmanTree** tree,int data)
{
    HuffmanTree* root  =  *tree;
    if(root==NULL)
    {
      perror("初始结点为空");
      return;
    }
    int rootData = *(root->data);
    HuffmanTree*  node = create_huffman_tree(data);   
    HuffmanTree*  newRoot = create_huffman_tree(data+rootData);  
    bool isLeft = rootData<data;
    newRoot->leftNode =  isLeft?root:node;
    newRoot->rightNode = isLeft?node:root;
    *tree =  newRoot;
}

void  pre_oder_huffmantree(HuffmanTree** tree)
{
   HuffmanTree* curNode = *tree;
   if(curNode==NULL)
   {
     return;
   }
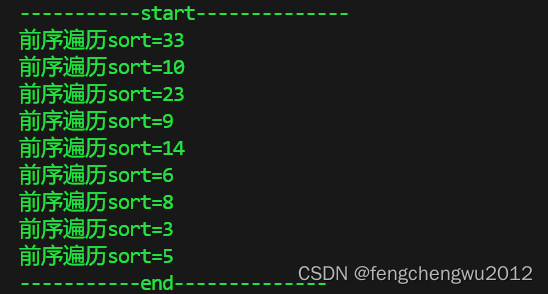
   printf("前序遍历sort=%d\n",*(curNode->data));
   pre_oder_huffmantree(&(curNode->leftNode));
   pre_oder_huffmantree(&(curNode->rightNode));
}


void  destroy_huffmantree(HuffmanTree* tree)
{
      if(tree==NULL)
      {
        return;
      }
      destroy_huffmantree(tree->leftNode);
      destroy_huffmantree(tree->rightNode);
      free(tree);
}

4、测试函数

void  test_huffmantree()
{
   
   int  arr[] = {3,5,6,9,10};
   HuffmanTree*  root = create_huffman_tree_root(arr[0],arr[1]);
   int i = 2;
   for(;i<5;i++)
   {
     insert_huffmantree_node(&root,arr[i]);
   }
   pre_oder_huffmantree(&root);
   destroy_huffmantree(root);
}