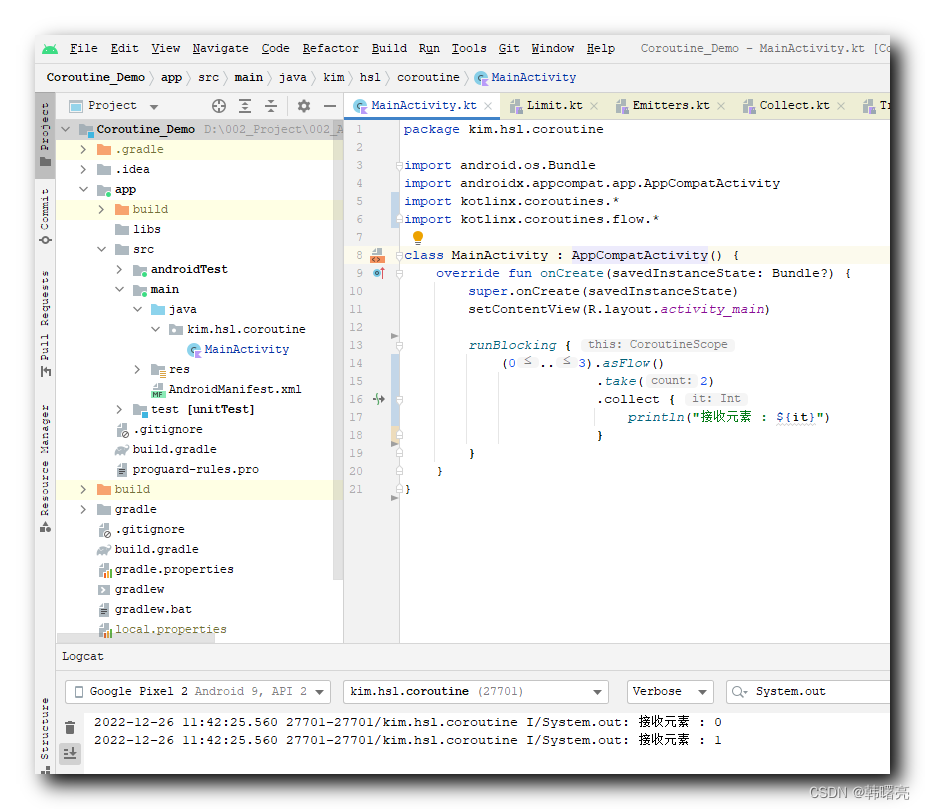
【Python】利用Python实现精准三点定位(经纬度坐标与平面坐标转换法求解)
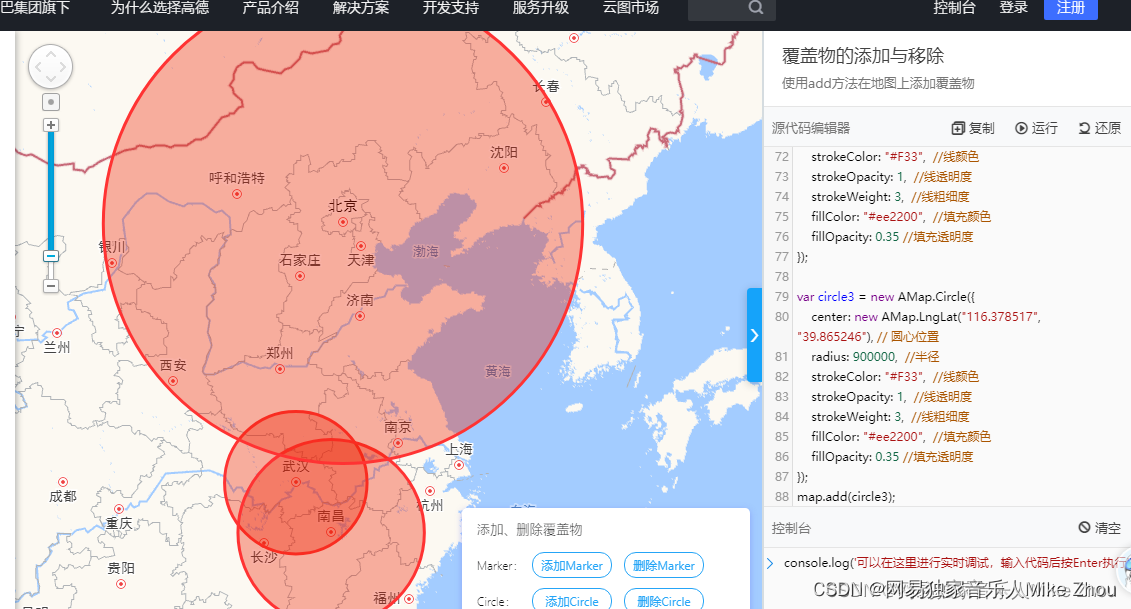
众所周知,如果已知三个点的坐标,到一个未知点的距离,则可以利用以距离为半径画圆的方式来求得未知点坐标。
如果只有两个已知点,则只能得出两个未知点坐标,而第三个圆必定交于其中一个点
如图:

三个圆必定教于一个点
当然,如果第三个绿色圆圆心位于红蓝的圆心连线上,则依然交于两个点,所以在选择对照点时,应尽可能使对照点分布在未知点四周,多取几个点位未尝不是一门好事
主要用到这两个库:
import math
import pyproj
pyproj是用于坐标转换的 这里采用的是utm平面坐标与WGS84经纬度坐标
这里的半径r单位都是米
高德地图用的是GCJ02坐标(还有腾讯) GPS用的是WGS84坐标(谷歌也是) 百度地图用的是BD09坐标
所以在实际计算出来导入地图里面查看时 要么采用WGS84地图 要么就要涉及到坐标转换
首先是坐标转换
在utm坐标中 有个zone值 也就是经度分区 计算公式为int(lon/6+31)
在反坐标转换中 也要输入zone值 这里直接可以输入转换前求得的zone值
def lonlat2utm(lon,lat):
z=int(lon/6+31)
proj = pyproj.Proj(proj='utm',zone=z,ellps='WGS84')
return proj(lon, lat),z
def utm2lonlat(x,y,z):
proj = pyproj.Proj(proj='utm',zone=z,ellps='WGS84')
return proj(x, y,inverse=True)
平面上求圆的交点
def insec(p1,r1,p2,r2):
x = p1[0]
y = p1[1]
R = r1
a = p2[0]
b = p2[1]
S = r2
d = math.sqrt((abs(a-x))**2 + (abs(b-y))**2)
if d > (R+S) or d < (abs(R-S)):
# print ("没有公共点")
return
elif d == 0 and R==S :
# print ("两个圆同心")
return
else:
A = (R**2 - S**2 + d**2) / (2 * d)
h = math.sqrt(R**2 - A**2)
x2 = x + A * (a-x)/d
y2 = y + A * (b-y)/d
x3 = round(x2 - h * (b - y) / d,2)
y3 = round(y2 + h * (a - x) / d,2)
x4 = round(x2 + h * (b - y) / d,2)
y4 = round(y2 - h * (a - x) / d,2)
c1=[x3, y3]
c2=[x4, y4]
return c1,c2
经纬度上求两个圆交点坐标
在反坐标转换中 也要输入zone值 这里直接可以输入转换前求得的两个经纬度坐标的zone平均值
所以 两个要求的区域离得不远 误差就很小 离得太远了 误差就可能大 需要手动去调整 这里是通用函数
def location_trans(p1,r1,p2,r2):
z1=lonlat2utm(p1[0],p1[1])
z2=lonlat2utm(p2[0],p2[1])
z=int((z1[1]+z2[1])/2)
C=insec(z1[0],r1,z2[0],r2)
if C:
a=utm2lonlat(C[0][0],C[0][1],z)
b=utm2lonlat(C[1][0],C[1][1],z)
c1=[a[0], a[1]]
c2=[b[0], b[1]]
return c1,c2
else:
return
运行:
a=[[114.304569,30.593354],300000]
b=[[115.857972,28.682976],400000]
c=[[116.378517,39.865246],900000]
print(location_trans(b[0],b[1],c[0],c[1]))
输出:
([114.12482189881902, 31.962881802790577], [117.87031764680636, 31.841927527011755])
在求三个圆的交点时 最多会求出六个点
在六个点中筛选出离另外一个圆最近的点 即可得出三个相近点的坐标
求离得近的那个点的平面坐标
def location_min(p1,p2,p,r):
d1=math.fabs(r-math.sqrt((p[0]-p1[0])**2+(p[1]-p1[1])**2))
d2=math.fabs(r-math.sqrt((p[0]-p2[0])**2+(p[1]-p2[1])**2))
if d1<d2:
return p1
else:
return p2
得到三个点后 求三个点的中心点 即可算出大概位置
中心点的zone值是根据其他三个zone值求平均来确定的
所以 三个要求的区域离得不远 误差就很小 离得太远了 误差就可能大 需要手动去调整 这里是通用函数
def location_judg(p1,r1,p2,r2,p3,r3):
li=[]
z1=lonlat2utm(p1[0],p1[1])
z2=lonlat2utm(p2[0],p2[1])
z3=lonlat2utm(p3[0],p3[1])
z12=int((z1[1]+z2[1])/2)
z13=int((z1[1]+z3[1])/2)
z23=int((z2[1]+z3[1])/2)
z=int((z12+z13+z23)/3)
C12=insec(z1[0],r1,z2[0],r2)
C13=insec(z1[0],r1,z3[0],r3)
C23=insec(z2[0],r2,z3[0],r3)
if C12:
m12=location_min(C12[0],C12[1],z3[0],r3)
li.append(utm2lonlat(m12[0],m12[1],z12))
else:
li.append(None)
if C13:
m13=location_min(C13[0],C13[1],z2[0],r2)
li.append(utm2lonlat(m13[0],m13[1],z13))
else:
li.append(None)
if C23:
m23=location_min(C23[0],C23[1],z1[0],r1)
li.append(utm2lonlat(m23[0],m23[1],z23))
else:
li.append(None)
if C12 and C13 and C23:
# print("三个坐标作的圆都有公共点")
m=[(m12[0]+m13[0]+m23[0])/3,(m12[1]+m13[1]+m23[1])/3]
li.append(utm2lonlat(m[0],m[1],z))
return li
elif C12 or C13 or C23:
# print("三个坐标作的圆不全有公共点")
li.append(None)
return li
else:
# print("三个坐标作的圆都没有公共点")
return
最后返回的列表分别是12的最接近坐标 13的最接近坐标 23的最接近坐标 和这三个坐标的中心点坐标 如果不存在 则返回None
运行:
if __name__ == "__main__":
a=[[114.304569,30.593354],300000]
b=[[115.857972,28.682976],400000]
c=[[116.378517,39.865246],900000]
print(location_trans(b[0],b[1],c[0],c[1]))
print(location_judg(a[0],a[1],b[0],b[1],c[0],c[1]))
结果:
[(116.85351953263574, 32.18782636821823), (117.13697531307241, 31.774218803048125), (117.87031764680636, 31.841927527011755), (117.28744847106574, 31.935380071325877)]
整体代码:
# -*- coding: utf-8 -*-
import math
import pyproj
def lonlat2utm(lon,lat):
z=int(lon/6+31)
proj = pyproj.Proj(proj='utm',zone=z,ellps='WGS84')
return proj(lon, lat),z
def utm2lonlat(x,y,z):
proj = pyproj.Proj(proj='utm',zone=z,ellps='WGS84')
return proj(x, y,inverse=True)
def insec(p1,r1,p2,r2):
x = p1[0]
y = p1[1]
R = r1
a = p2[0]
b = p2[1]
S = r2
d = math.sqrt((abs(a-x))**2 + (abs(b-y))**2)
if d > (R+S) or d < (abs(R-S)):
# print ("没有公共点")
return
elif d == 0 and R==S :
# print ("两个圆同心")
return
else:
A = (R**2 - S**2 + d**2) / (2 * d)
h = math.sqrt(R**2 - A**2)
x2 = x + A * (a-x)/d
y2 = y + A * (b-y)/d
x3 = round(x2 - h * (b - y) / d,2)
y3 = round(y2 + h * (a - x) / d,2)
x4 = round(x2 + h * (b - y) / d,2)
y4 = round(y2 - h * (a - x) / d,2)
c1=[x3, y3]
c2=[x4, y4]
return c1,c2
def location_trans(p1,r1,p2,r2):
z1=lonlat2utm(p1[0],p1[1])
z2=lonlat2utm(p2[0],p2[1])
z=int((z1[1]+z2[1])/2)
C=insec(z1[0],r1,z2[0],r2)
if C:
a=utm2lonlat(C[0][0],C[0][1],z)
b=utm2lonlat(C[1][0],C[1][1],z)
c1=[a[0], a[1]]
c2=[b[0], b[1]]
return c1,c2
else:
return
def location_min(p1,p2,p,r):
d1=math.fabs(r-math.sqrt((p[0]-p1[0])**2+(p[1]-p1[1])**2))
d2=math.fabs(r-math.sqrt((p[0]-p2[0])**2+(p[1]-p2[1])**2))
if d1<d2:
return p1
else:
return p2
def location_judg(p1,r1,p2,r2,p3,r3):
li=[]
z1=lonlat2utm(p1[0],p1[1])
z2=lonlat2utm(p2[0],p2[1])
z3=lonlat2utm(p3[0],p3[1])
z12=int((z1[1]+z2[1])/2)
z13=int((z1[1]+z3[1])/2)
z23=int((z2[1]+z3[1])/2)
z=int((z12+z13+z23)/3)
C12=insec(z1[0],r1,z2[0],r2)
C13=insec(z1[0],r1,z3[0],r3)
C23=insec(z2[0],r2,z3[0],r3)
if C12:
m12=location_min(C12[0],C12[1],z3[0],r3)
li.append(utm2lonlat(m12[0],m12[1],z12))
else:
li.append(None)
if C13:
m13=location_min(C13[0],C13[1],z2[0],r2)
li.append(utm2lonlat(m13[0],m13[1],z13))
else:
li.append(None)
if C23:
m23=location_min(C23[0],C23[1],z1[0],r1)
li.append(utm2lonlat(m23[0],m23[1],z23))
else:
li.append(None)
if C12 and C13 and C23:
# print("三个坐标作的圆都有公共点")
m=[(m12[0]+m13[0]+m23[0])/3,(m12[1]+m13[1]+m23[1])/3]
li.append(utm2lonlat(m[0],m[1],z))
return li
elif C12 or C13 or C23:
# print("三个坐标作的圆不全有公共点")
li.append(None)
return li
else:
# print("三个坐标作的圆都没有公共点")
return
if __name__ == "__main__":
a=[[114.304569,30.593354],300000]
b=[[115.857972,28.682976],400000]
c=[[116.378517,39.865246],900000]
print(location_trans(b[0],b[1],c[0],c[1]))
print(location_judg(a[0],a[1],b[0],b[1],c[0],c[1]))
参考图如下: