选择图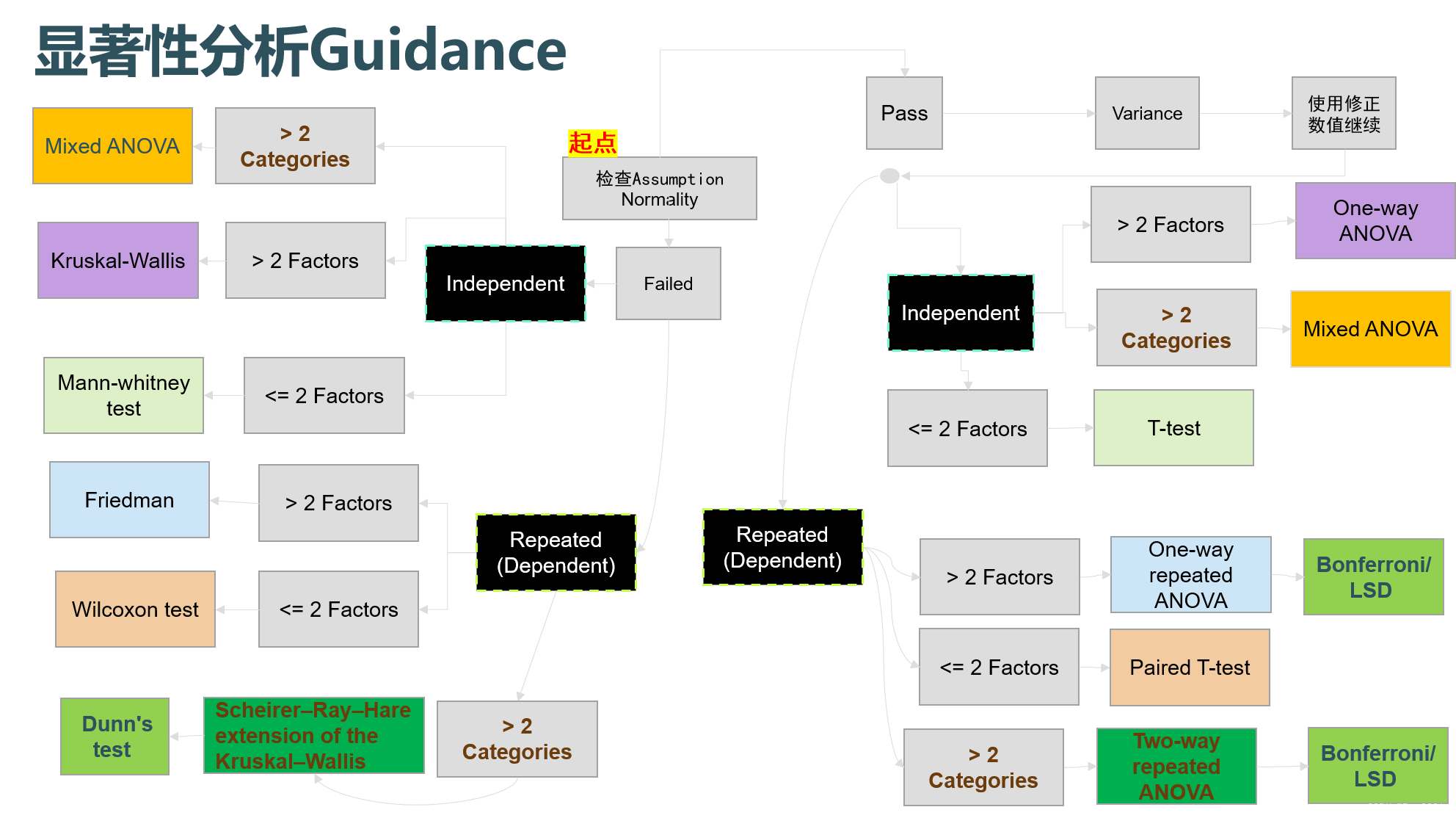
为什么要分Non-parametric & parametric 方法
为了找到更符合数据的分析方法。每个方法有自己的假设,如果违背了结果会不精准。
Sign Test 是一个可以用于任何数据分布情况的pairwise 方法。
检查normality:
Sample 数量 < 50,适用 Shapiro-Wilk,Sample 数量 >= 50,适用Kolmogorov-Smirnov
Within subject Vs. Between subjects
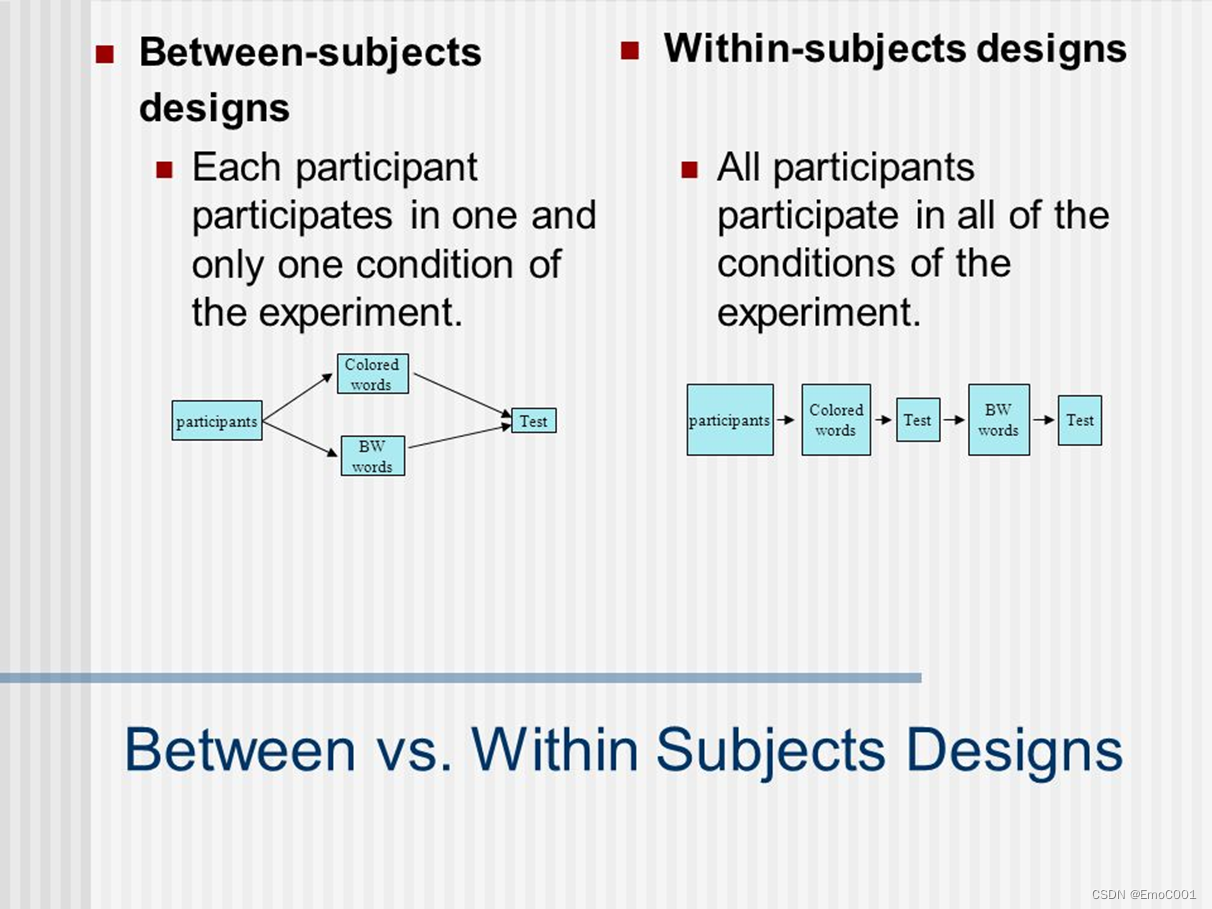
为什么要用post-hoc方法
历史遗留问题:LSD是当年可以和ANOVA搭配使用的两两比较方法,并且需要ANOVA的F test
• 所以称这样从多个比较里进行两两比较的为post hoc
• 对于parametric 的 ANOVA 或者 non-parametric 的 Kruskal-Wallis, post-hoc 一般还选Bonferroni, Tukey,Dunnett
• 但这些方法和LSD一样需要基于ANOVA/Kruskal 的结果
• 但是,目前有越来越多的方法可以用于ANOVA计算前/后,anytime,不受ANOVA限制。主要是两两比较也很重要。例如:Wilcoxon-Rank & T(或 paired) test, sign test
• 从ANOVA这种算global significance的到post-hoc(两两比较)的方法,都有自己的假设条件,只有满足了这些假设条件,才能使用,不然算“违规操作”~
要使用什么样的数据进行分析
数据是由一堆视频得到的:
方法一:平均
“Note that although SI is a discrete variable, its value per quadruplet is averaged over all (about 48,000) frames per recording. Therefore it is statistically treated as a continuous variable”[1]
[2]
方法二: SUM
用了total absolute turn angle, total meandering…[3]
[1]: Assessing Social Engagement in Heterogeneous Groups of Zebrafish: A New Paradigm for Autism-Like Behavioral Responses
[2]:Measures of Anxiety in Zebrafish (Danio rerio): Dissociation of Black/White Preference and Novel Tank Test
[3]:Differences in Spatio-Temporal Behavior of Zebrafish in the Open Tank Paradigm after a Short-Period Confinement into Dark and Bright Environments
分析对象不是数据本身而是被实验物
Non-parametric for Two-Way ANOVA
Scheirer–Ray–Hare extension of the Kruskal–Wallis test
下载并安装 R:[1,2]https://cloud.r-project.org/
[1] https://blog.csdn.net/weixin_39603537/article/details/111334296
[2] https://rcompanion.org/handbook/F_14.html
data <- read.csv(file = "C:\\Users\\Windows\\Desktop\\显著性分析\\depth\\3_14_4.CSV", header = TRUE, sep = ",")
print(data)
library(rcompanion)
scheirerRayHare(depth~exp*time, data = data)
文件输出的参数名字 <- read.csv(file = “用\\ 隔开的文件地址", header = TRUE, sep = ",")
print(data)
library(加载需要调用的package)
scheirerRayHare(depth~exp*time, data =文件输出的参数名字 )
Wilcoxon 的asymmetry检测
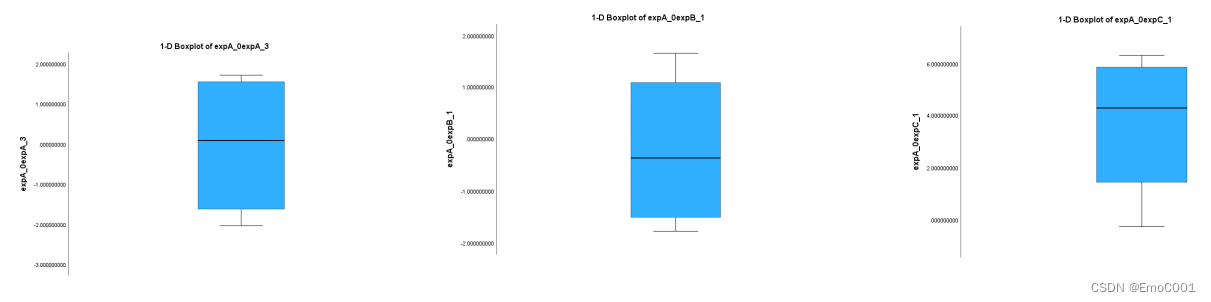
随机抽取了几组数据,发现第二和第三组严重不达标Wilcoxon的(蓝色块的中线明显skewed), 要用Sign Test(退而求其次)
Variance 检查
凡是关于repeated的实验,都用mauchly’s test.否则用levene’s test。
Sphericity p-value 没有值原因:我们的数据量只有4个实验对象,而condition的数量超过了实验对象的数量
当variance不达标可以使用Greenhouse-Geisser 等类似以下列出的correction values 作为最终的p-value
数据是百分比
The following rules may be useful in choosing the proper transformation scale for the percentage data derived from count data.
• Rule 1. For percentage data lying within the range of 20 - 80%, no transformation is needed.
• Rule 2. For percentage data lying within a range of either 0 - 20% or 80 – 100%, but not both, the square root transformation could be useful.
• Rule 3. For percentage data that do not follow the ranges specified in either Rule 1 or Rule 2 (e.g.percent control data), the Arc Sine square root transformation may be useful.
Arc sine square root transformation - ArcSine (Y)1/2
Appropriate for data on proportions, binomial data, and data expressed as percent of control.
The value of 0% should be substituted by (1/4n) and the value 100% by (100-1/4n), where n is the number of units in which the percentage data were based (i.e. the denominator used in computing the percentage.
Logarithmic (Log10) transformation
Appropriate for data where the standard deviation is proportional to the mean.
Helpful when the data are expressed as a percentage of change.
These types of data may follow a multiplicative model instead of an additive model.
If the data set includes small values (e.g. less than 10), use the transformation Log(Y+1) instead of Log Y(Y is the original data).
Square root transformation
Useful for count data (data that follow a Poisson distribution).
Appropriate for data consisting of small whole numbers. In both these cases the mean may be proportional to the variance.
Examples are the number of infested plants per plot, the number of insects caught in a trap, the number of weeds per plot (i.e. data obtained in counting rare events).
This transformation also may be appropriate for percentage data where the range is between 0 and 20% or between 80 and 100%.
If most of the values in the data set are less than 10, especially if zeros are present, the transformation to use is (Y+0.5)1/2 instead of Y1/2.
Bonferroni Vs. Fisher’s Least Significant Difference (LSD)
LSD 的数值敏感度高于 Bonferroni
Bonferroni 适用于<=5的情景,当情景有>=6,改用 Tukey
使用情况:
- 当ANOVA得到global的显著性时,但使用传统的Bonferroni没有得到,改用LSD
• 如果ANOVA没有得到global的显著性,不可以使用LSD碰运气哦:
• 违反LSD的assumption
• LSD的post-hoc计算需要用到ANOVA里 mean-square within 的结果
如果ANOVA不显著,如何做pairwise comparisons?
- Wilcoxon
- Sign
- McNemar (>=30条鱼)