算法：二叉树难题和与STL相结合的练习题

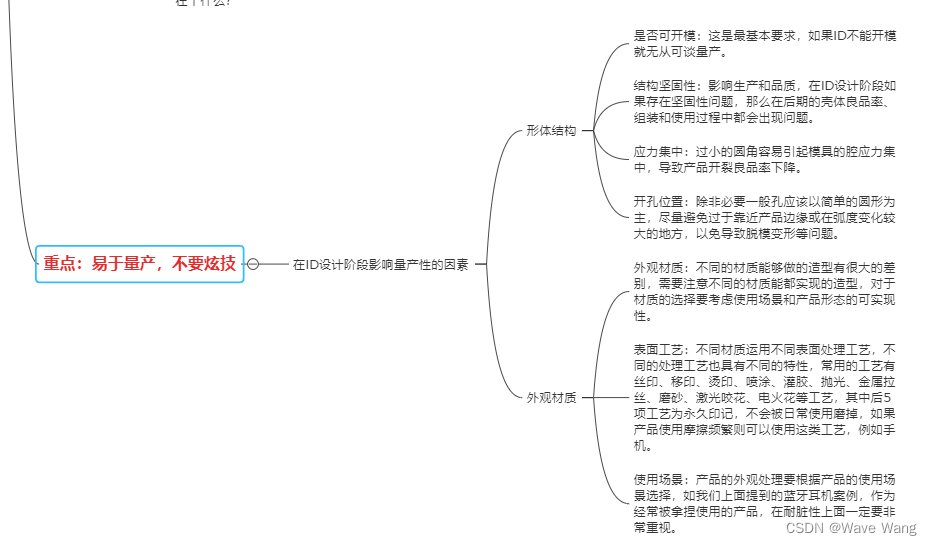
文章目录

二叉树层序遍历原理
- 二叉树的层序遍历
二叉树的最近公共祖先
二叉搜索树和双向链表
从前序与中序遍历序列构造二叉树
从后序与中序遍历序列构造二叉树
二叉树的非递归实现
- 前序遍历
- 中序遍历
- 后序遍历

二叉树层序遍历原理

二叉树的层序遍历通常是借助队列来实现，可以将二叉树的根节点放入队列中，每当要出队列的时候就将这个要出的节点的左右节点入队列，这样就可以实现一层带着一层实现一个层序遍历的效果，当队列为空的时候就说明全部遍历结束了，也就终止了程序

void levelorder(TreeNode* root)
{
	vector<int> v;
	queue<TreeNode*> q;
	q.push(root);
	while (!q.empty())
	{
		TreeNode* node = q.front();
		q.pop();
		v.push_back(node->val);
		if (node->left)
			q.push(node->left);
		if (node->right)
			q.push(node->right);
	}
}

二叉树的层序遍历

层序遍历需要借助队列来使用，但是这个题并不仅仅是需要队列，题目要求需要保存在二维数组中，因此和前面的还略有不同，首先需要把数组创建出来，创建出来之后还需要知道每一层节点的个数，这个个数可以通过队列中的元素个数来决定，例如一开始根入队列，那么队列中元素为1，也就意味着数组中第一行元素个数为1个，而当第一个元素出队列同时带入第二层的元素的时候，队列元素也会更新，根据这个元素个数就可以得出这层的元素个数等等…

class Solution 
{
public:
    vector<vector<int>> levelOrder(TreeNode* root) 
    {
        // 创建一个vector用来返回结果，一个queue用来记录每一层节点的信息
        vector<vector<int>> v;
        queue<TreeNode*> q;
        
        // 判断特殊情况
        if(root == nullptr)
            return v;

        // 首先把根入队列
        q.push(root);
        
        // 开始循环过程
        while(!q.empty())
        {
            // 记录这一层中有多少个节点需要被放到vector中存储信息
            int size = q.size();
            // 为这一层的信息开辟对应vector中的空间
            v.push_back(vector<int> {});
            for(int i = 0;i < size; i++)
            {
                // 取到队列的头，并出队列
                TreeNode* node = q.front();
                q.pop();
                // 记录当前出去的队列元素的信息
                v.back().push_back(node->val);
                // 记录它的孩子
                if(node->left)
                    q.push(node->left);
                if(node->right)
                    q.push(node->right);
            }
        }

        return v;
    }
};

二叉树的最近公共祖先

思路1：通过规律来寻求答案

通过观察几个例子其实可以看出，这两个结点一定分布在它们祖先的左右子树，因此可以使用这样的思路：假设现在要找的节点是p和q，如果现在能找到这样一个结点，使得p和q分别分布在它的左右子树，那么这个结点就是要找的公共结点，或者另外一种情况是，其中一个就是当前树的根，就是上面图中的最后一种情况

因此思路就出来了，判断当前p是在当前结点的哪个子树，如果p和q都是左子树，那么就把根转移到左子树中进行搜索，如果p和q都在右子树，那么就把根转移到右子树中进行搜索，如果是一左一右，就说明情况正确了

class Solution 
{
public:
    bool Check(TreeNode* root, TreeNode* p)
    {
        // 递归终止条件，如果根节点为空就是没找到，如果根节点就是p，则说明找到了
        if(root == nullptr)
            return false;
        if(root == p)
            return true;
        
        // 在左右子树中遍历寻找
        return Check(root->left, p) || Check(root->right, p);
    }

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) 
    {
        // 如果根就是p和q中的一个，说明p和q中的一个就是公共祖先
        if(root == p || root == q)
            return root;
        
        // 判断当前情况下，p在根的左子树还是右子树
        bool pInleft = Check(root->left, p);
        bool pInright = !pInleft;

        // 判断当前情况下，q在根的左子树还是右子树
        bool qInleft = Check(root->left, q);
        bool qInright = !qInleft;

        // 如果正好是一左一右，说明找到了
        if((pInleft && qInright) || (pInright && qInleft))
            return root;
        
        // 如果都在左子树，那么就转移到根的左子树进行搜索
        if(pInleft && qInleft)
            return lowestCommonAncestor(root->left, p, q);
        
        // 如果都在右子树，那么就转移到根的右子树进行搜索
        if(pInright && qInright)
            return lowestCommonAncestor(root->right, p, q);

        // 保证所有路径都有返回值
        return nullptr;
    }
};

这样的做法是可以通过测试用例的，但是时间复杂度很高，在极端情况下，它的时间复杂度是趋近于O(n^2)的，因此下面用一种和STL相结合的方法来解决

思路2：想办法描述出从根节点到所求节点的路径，这两个结点的路径的交叉点就是最近公共祖先

这种思路是把二叉树看成了一个链表来看，相当于现在转换成了要求链表的最近交叉点，对于描述出根节点到所求节点的路径，可以转换成用一个栈的容器来装各个节点，每遍历一个节点就push到栈中，如果发生了回溯就pop掉当前的节点，然后最终得到的栈中的元素顺序就是所求的路径

class Solution 
{
public:
    bool getPath(TreeNode* root, TreeNode* p, stack<TreeNode*>& sk)
    {
        // 递归终止条件：当root为空则说明要到另外部分去寻找结果
        if(root == nullptr)
            return false;
        
        // 首先push根节点
        sk.push(root);

        // 如果找到了节点，那么就返回找到了
        if(root == p)
            return true;

        // 接着在左子树中寻找目标节点
        if(getPath(root->left, p, sk))
            return true;

        // 接着在右子树中寻找目标节点
        if(getPath(root->right, p, sk))
            return true;

        // 如果在左右子树中都没找到节点，那么就要回溯到前面的节点，就要先恢复现场
        sk.pop();
        return false;
    }

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) 
    {
        // 创建两个栈，分别得到两个节点的路径信息
        stack<TreeNode*> pPath;
        stack<TreeNode*> qPath;
        getPath(root, p, pPath);
        getPath(root, q, qPath);

        // 首先让两个栈的大小相同
        while(pPath.size() != qPath.size())
        {
            if(pPath.size() > qPath.size())
                pPath.pop();
            else
                qPath.pop();
        }

        // 接着寻找最近公共祖先
        while(pPath.top() != qPath.top())
        {
            pPath.pop();
            qPath.pop();
        }

        // 此时得到的栈的顶端元素就是最近的相交节点，也就是所求的节点
        return pPath.top();
    }
};

这个时间复杂度就比较相对较低，也是比较好的一种方法

二叉搜索树和双向链表

解决这个问题，首先要看懂题的意思，题意中明确写到，树的节点的左指针需要指向前驱，树的节点的右指针需要指向后继，那么就需要找到前驱和后继，因此起码至少需要两个指针，一个指向前驱，一个指向后继，执行的关键操作就是

cur->left = prev;
prev->right = cur;

这里巧妙运用了前驱和后继，并不是单独定义一个指针和前驱还有后继，而是将这三个指针合并为两个，令前驱指向后继，后继指向前驱，形成了一个一层一层链接起来的效果

class Solution 
{
public:
	void InOrder(TreeNode* cur, TreeNode*& prev)
	{
		if(cur == nullptr)
			return;
		InOrder(cur->left, prev);
		cur->left = prev;
		if(prev)
			prev->right = cur;
		prev = cur;
		InOrder(cur->right, prev);
	}

    TreeNode* Convert(TreeNode* pRootOfTree) 
	{
		if(pRootOfTree == nullptr)
			return nullptr;
        TreeNode* cur = pRootOfTree;
		TreeNode* prev = nullptr;
		InOrder(cur, prev);
		while(cur->left)
		{
			cur = cur->left;
		}
		return cur;
    }
};

下图是递归展开图，里面画出了递归的过程以及prev使用引用的含义，构思巧妙的可以解决这个问题

从前序与中序遍历序列构造二叉树

此题考查的是关于二叉树前序遍历和中序遍历的理解，前序遍历的遍历顺序是根，左子树，右子树，中序遍历的顺序是左子树，根，右子树，因此可以理解成，前序遍历中的每一个节点都可以看成一个根，而这个值在中序遍历中进行划分，划分出来的结果左边就是左子树，右边就是右子树，因此在设计递归函数头的时候，第一个是要在前序遍历中找到根的下标，其次是在中序遍历中要找到这个根所在位置的下标，这样就能划分出左右两个区间，而这两个区间就代表着左子树的区间和右子树的区间

而递归的终止条件也就因此而引出来了，当子树区间不存在的时候，就说明已经走到叶子节点了，对于叶子节点的左右子树按空处理即可

从后序与中序遍历序列构造二叉树

总体来说思路和前面基本一致，只不过寻找根要倒着寻找，同时要先构建右子树，再构建左子树，因为后序遍历的顺序是左子树，右子树，根，因此找到根后先遇到的是右子树

class Solution 
{
public:
    TreeNode* _buildTree(vector<int>& inorder, vector<int>& postorder, int& posti, int inbegin, int inend) 
    {
        if(inbegin > inend)
            return nullptr;
        int rooti = inend;
        // 后序遍历的根在中序遍历中去寻找
        while(inbegin <= inend)
        {
            if(postorder[posti] == inorder[rooti])
                break;
            rooti--;
        }
        // [inbegin,rooti-1]rooti[rooti+1,inend]
        TreeNode* root = new TreeNode(postorder[posti--]);
        root->right = _buildTree(inorder, postorder, posti, rooti+1, inend);
        root->left = _buildTree(inorder, postorder, posti, inbegin, rooti-1);
        return root;
    }

    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) 
    {
        int posti = postorder.size()-1;
        TreeNode* root = _buildTree(inorder, postorder, posti, 0, inorder.size()-1);
        return root;
    }
};

二叉树的非递归实现

二叉树的非递归实现一般是借助栈来实现的，前序和中序较为简单，后序遍历相比起来较为繁琐，但都是借助栈来实现的二叉树的遍历

对于二叉树的前序遍历通常借助栈的实现思路是，将节点保存在栈中，一直遍历左子树直到遇到没有左子树的根，此时就进行遍历右子树，右子树中对上面的操作进行迭代，如果这个此时这个节点也没有右子树，也就是说这个节点是叶子节点，那么就要进行回溯的过程，而进行回溯的过程就是把已经入栈的这些节点进行出栈的过程

前序遍历

class Solution 
{
public:
    vector<int> preorderTraversal(TreeNode* root) 
    {
        // 一个vector用于存储遍历后的值，一个栈用于辅助遍历节点
        vector<int> v;
        stack<TreeNode*> sk;
        TreeNode* cur = root;
        
        // 只有当节点值为空并且栈也为空的时，说明遍历结束了
        while(cur || !sk.empty())
        {
            // 一直访问根的左节点，直到叶子节点
            while(cur)
            {
                // 把遍历的结果入栈和vector中，然后迭代
                sk.push(cur);
                v.push_back(cur->val);
                cur = cur->left;
            }

            // 运行到这里的时候，已经到了没有左子树的节点了，此时这个节点可能有右子树，因此要访问它的右子树
            TreeNode* node = sk.top();
            sk.pop();
            // 令cur为此时节点的右子树，则转移到右子树中进行迭代的问题
            cur = node->right;
        }
        return v;
    }
};

中序遍历

二叉树的中序遍历和前序遍历的区别是，中序遍历优先记录的是左子树，记录左子树后才记录根，因此唯一的区别就是在把节点的值记录的时候，要在出栈的过程中记录，而不是在入栈的过程中记录

class Solution 
{
public:
    vector<int> inorderTraversal(TreeNode* root) 
    {
        vector<int> v;
        stack<TreeNode*> sk;
        TreeNode* cur = root;
        while(cur || !sk.empty())
        {
            while(cur)
            {
                sk.push(cur);
                cur = cur->left;
            }

            TreeNode* node = sk.top();
            sk.pop();
            v.push_back(node->val);
            cur = node->right;
        }
        return v;
    }
};

后序遍历

对于后序遍历来说，和前面的区别是，要先遍历右子树才能遍历根，因此当左子树遍历完成后，不能急于将节点信息进行存储，而是要进行判断，如果这个节点没有右节点，或者节点已经被遍历了，此时就轮到遍历根节点了，而对于如何知道右节点有没有被遍历可以使用一个prev指针，如果是第一次遍历这个节点的时候，此时prev节点一定不会被遍历，如果是第二次遍历到这个根节点，就说明这个根是从右子树遍历后回到了这个根节点，对于prev的标记应该要在遍历根节点后，就说明这个节点已经被遍历过了，使用prev进行标记即可

class Solution 
{
public:
    vector<int> postorderTraversal(TreeNode* root) 
    {
        vector<int> v;
        stack<TreeNode*> sk;
        TreeNode* cur = root;
        TreeNode* prev = nullptr;
        while(cur || !sk.empty())
        {
            // 一直遍历左子树，直到遇到没有左子树的节点
            while(cur)
            {
                sk.push(cur);
                cur = cur->left;
            }

            TreeNode* node = sk.top();
            // 此时取栈顶节点，也就是最后一个左子树节点，如果这个节点没有右子树或者这个节点的右子树已经被遍历过了，就将这个节点的信息放到vector中
            if(node->right == nullptr || node->right == prev)
            {
                sk.pop();
                v.push_back(node->val);
                prev = node;
            }
            // 如果节点有右子树,那么就要先遍历右子树,再遍历根
            else
            {
                cur = node->right;
            }
        }
        return v;
    }
};