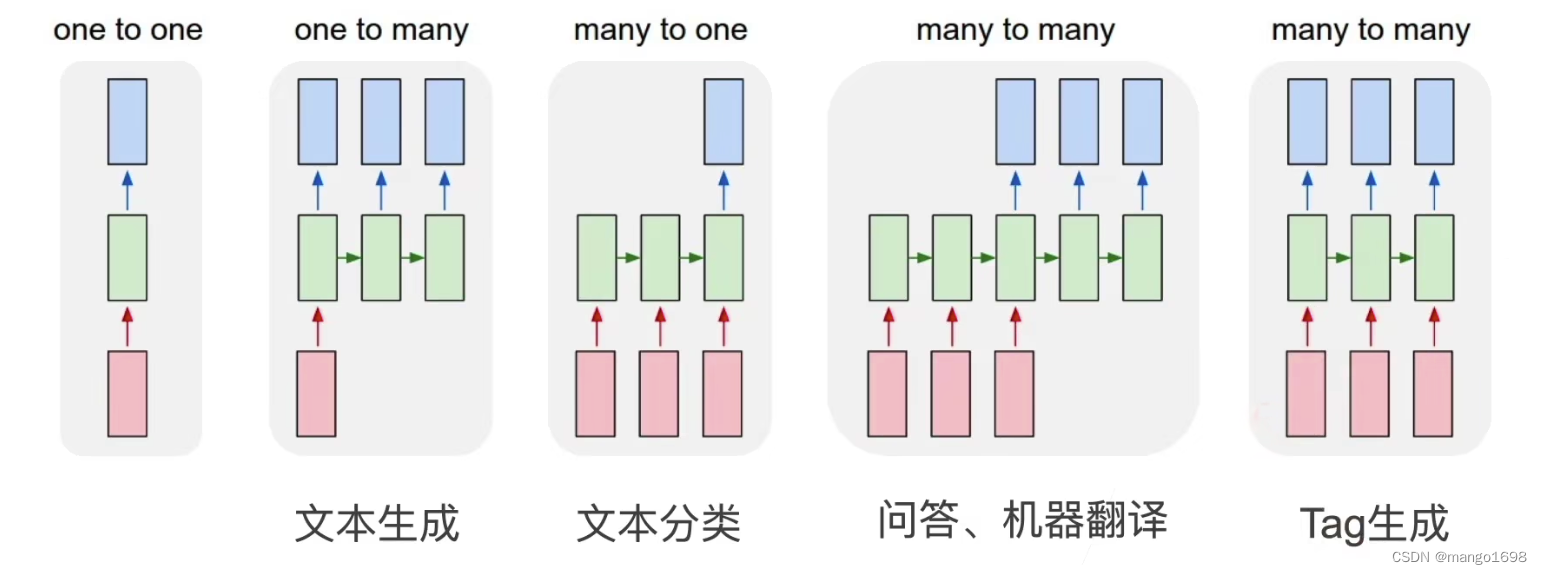
这里我们将探索神经元/单元和层的内部工作原理。特别是,与之前学习的回归/线性模型和逻辑模型进行比较。最后接介绍tensorflow以及如何利用tensorflow来实现这些模型。
神经网络和大脑的神经元工作原理类似,但是比大脑的工作原理要简单的多。大脑中神经元的工作原理如下图:inputs表示上一个神经元传递过来的信号,然后经过当前神经元的处理,当前神经元将处理后的信号传递给下一个神经元,这样基本的信号传递就完成了。

神经网络的结构
machine learning的神经网络结构类似于大脑的神经网络结构,下图中向量x为上一层的输入,包含三个蓝色圆圈的黑色方框是当前的处理层,向量a[1]为当前层的输出,并且问下一层的输入,向量a[2]为最终的输出结果。可以看到一个简单的神经网络由输入层、处理层、输出层组成,其中处理层中可以包含多个处理的“神经元”,处理层也叫做隐藏层。

更复杂的神经网络包含多个处理层,如下图,包含两个处理层:
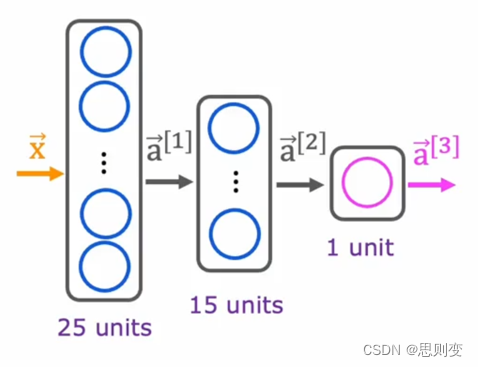
输入层
输入训练数据的作用
处理层
处理层中包含多个神经元,每一个神经元就是一个处理模型,比如说线性回归模型,逻辑回归模型或者sigmoid激活函数。

比如上面的处理层a[1]有3个神经元(unit表示神经元),那么layer_1中包含3个unit,并且都是sigmoid激活函数。输出层a[2]有一个神经元,那么layer_2中unit为1,模型为sigmoid激活函数
那么怎么将各层之间的输入与输出联系起来呢?Sequential 会将所有的层按线性连接起来形成module,如下图
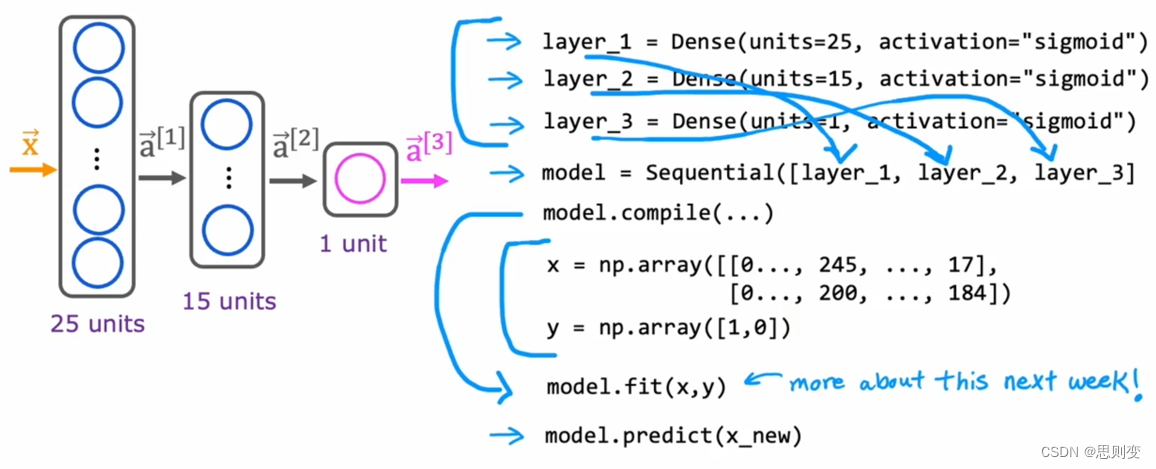
这种上一层的输出结果作为下一层的输入,并计算下一层的输出,直到计算到输出层为止,被叫做前向传播(forward)。 前向传播的一般实现为:
import numpy as np
W = np.array([[1,-3,5]
[2,4,-6]])
b = np.array([-1,1,2])
a_in = np.arry([-2,4])
def dense(a_in,W,b,g):
units = W.shape[1]
a_out = np.zeros(units)
for j in range(units):
w= W[:,j]
z = np.dot(w,a_in) + b[j]
a_out[j]=g(z)
return a_out
def sequential(x):
a1 = dense(x,W[1],b[1])
a2 = dense(a1, W[2], b[2])
a3 = dense(a2, W[3], b[1])
a4 = dense(a3, W[4], b[1])
f_x = a4
return f_x













![[NISACTF 2022]join-us 无列名注入 过滤database() 报错获取表名 字段名](https://img-blog.csdnimg.cn/b74ce9faa576410ea7168849d07aa9ab.png)