当我们打开一份有十几列，几万行的明细数据时，那种感觉我相信用铺天盖地、头晕目眩来形容是再合适不过了。

面对如此令人崩溃的场景，必须要求我们要求能够快速找到数据的特征。描述性统计正是为此而生，它通过几个简单的分析方法就能在几秒钟内提取出指标背后的数据特征，快速建立整体全面的认知，并帮助我们寻找到分析的突破口。

为了能够高效的发现数据的特征，描述性统计为我们提供了三个非常有用的分析工具，分别是：

• 中位数/平均数

• 方差/标准差

分析工具1：用中位数和平均数分析数据分析布情况

平均数一般包括算数平均数和几何平均数：

        算数平均数：适用于指标是绝对值的数据；比如（1+2+3+4）/4

        几何平均数：适用于指标是百分比的数据。比如 （11%+12%+13%+14%）开5次方

中位数和平均数一般结合着使用。先看下面一组数据。

• 产品 A 的日均销售额为 281.11，每日销售额的中位数是 234，即平均数大于中位数。
  意味着产品 A 的每日销售额偏高的居多，可能是产品 A 的客单价较高，可能是某一天的销售额很高，拉高了平均数。

• 产品 B 的日均销售额为 281.11，每日销售额的中位数是 315，即平均数小于中位数。
  意味着产品 B 的每日销售额偏低的居多，可能是产品 B 的客单价较低，可能是某一天的销售额很低，拉低了平均数。

分析工具 2：用“方差和标准差”来分析指标的波情况

方差，是指数据的离散程度，是一组数据与这组数据平均数之差的平方值的平均数；而标准差，是方差的开方值。

• 方差和标准差代表了业务指标的波动情况，即业务稳定性的高低，也即业务经营风险的大小；

• 当方差和标准差变大，意味着指标波动变大，业务稳定性降低，业务经营风险升高；

• 当方差和标准差变小，意味着指标波动变小，业务稳定性升高，业务经营风险降低；

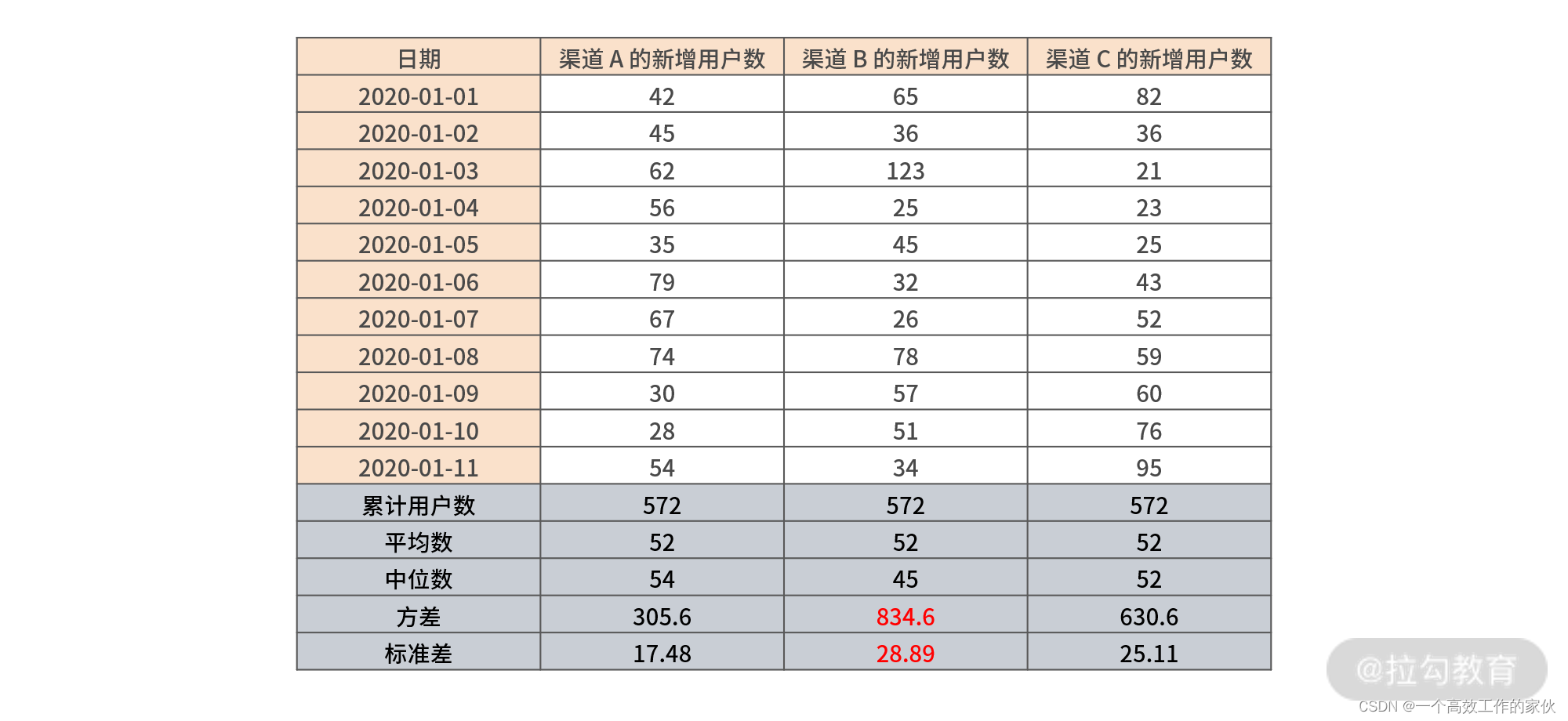
 我们用方差来计算，分别计算这三个渠道的每日获客量的方差和标准差：

• 渠道 A 的每日新增用户数的方差是 305.6，标准差是 17.48；

• 渠道 B 的每日新增用户数的方差是 834.6，标准差是 28.89；

• 渠道 C 的每日新增用户数的方差是 630.6，标准差是 25.11。

我们发现：因为渠道 B 的每日新增用户数方差和标准差最大，可以认为在这 3 个渠道中，渠道 B 的获客能力波动最大，稳定性最差，后续的风险也在 3 个渠道中最高（相对），接下来的运营需要更多的关注渠道 B 的运营情况；而渠道 A 和渠道 C 的获客能力相对波动较小，获客较稳定，保持中优先级的关注即可。